【高考专辑】【专题14】2015年高三数学(理)【押题精练】概率与统计
文档属性
| 名称 | 【高考专辑】【专题14】2015年高三数学(理)【押题精练】概率与统计 |  | |
| 格式 | zip | ||
| 文件大小 | 538.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 18:40:23 | ||
图片预览









文档简介
课件68张PPT。专题14
概率与统计天津南开市2015届高三 概率与统计要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.随机抽样方法
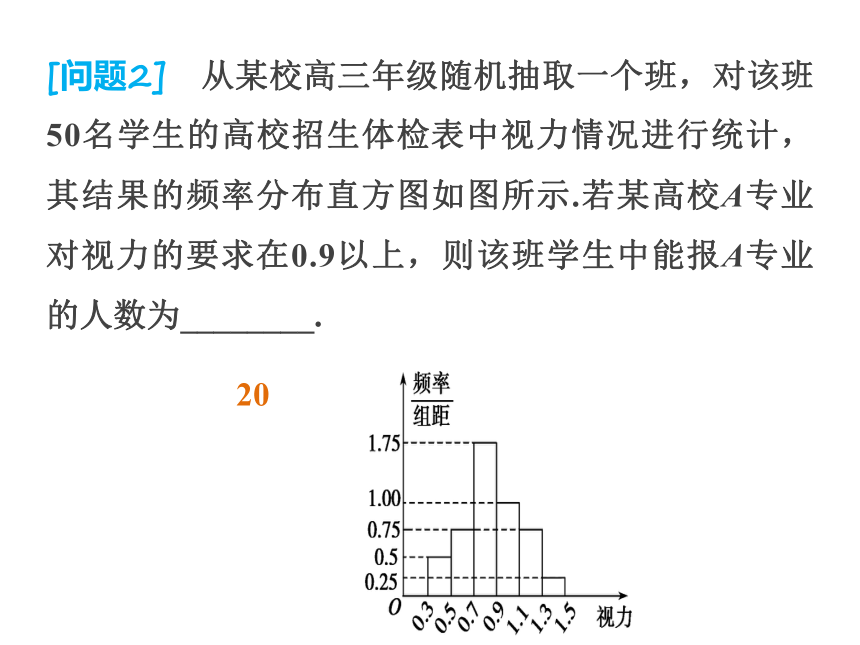
简单随机抽样、系统抽样、分层抽样的共同点是抽样过程中每个个体被抽取的机会相等,且是不放回抽样.[问题1] 某社区现有480个住户,其中中等收入家庭200户、低收入家庭160户,其他为高收入家庭.在建设幸福社区的某次分层抽样调查中,高收入家庭被抽取了6户,则该社区本次抽取的总户数为________.242.对于统计图表问题,求解时,最重要的就是认真观察图表,从中提取有用信息和数据.对于频率分布直方图,应注意的是图中的每一个小矩形的面积是数据落在该区间上的频率.茎叶图没有原始数据信息的损失,但数据很大或有多组数据时,茎叶图就不那么直观、清晰了.[问题2] 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为________.203.众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数为频率分布直方图中最高矩形的底边中点的横坐标.
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
平均数:样本数据的算术平均数,即 (x1+x2+…+xn).
平均数等于频率分布直方图中每个小矩形的面积乘以小距形底边中点的横坐标之和.平均数等于频率分布直方图中每个小矩形的面积乘以小距形底边中点的横坐标之和.
标准差的平方就是方差,方差的计算[问题3] 已知一个样本中的数据为0.12,0.15,0.13,0.15,0.14,0.17,0.15,0.16,0.13,0.14,则该样本的众数、中位数分别是____________.0.15、0.1455.独立性检验的基本方法
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表如表:根据观测数据计算由公式k=
所给出的检验随机变量K2的观测值k,并且k的值越大,说明“X与Y有关系”成立的可能性越大,可以利用数据来确定“X与Y有关系”的可信程度.[问题5] 为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:则至少有________的把握认为喜爱打篮球与性别有关.(请用百分数表示)99.5%6.互斥事件有一个发生的概率P(A+B)=P(A)+P(B)
(1)公式适合范围:事件A与B互斥.
(2)P( )=1-P(A).7.古典概型
P(A)= (其中,n为一次试验中可能出现的结果总数,m为事件A在试验中包含的基本事件个数)[问题7] 若将一枚质地均匀的骰子先后抛掷2次,则出现向上的点数之和为4的概率为________.[问题8] 在棱长为2的正方体ABCD—A1B1C1D1中,点O为底面ABCD的中心,在正方体ABCD—A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为( )解析 记“点P到点O的距离大于1”为A,答案 B9.解排列、组合问题的依据是:分类相加,分步相乘,有序排列,无序组合.
解排列、组合问题的规律是:相邻问题捆绑法;不相邻问题插空法;多排问题单排法;定位问题优先法;定序问题倍缩法;多元问题分类法;有序分配分步法;综合问题先选后排法;至多至少问题间接法.[问题9] (1)将5封信投入3个邮筒,不同的投法共有________种.
(2)从4台甲型和5台乙型电视机中任意取出3台,其中至少要甲型和乙型电视机各一台,则不同的取法共有________种.70特别提醒:二项式系数最大项与展开式系数最大项是两个不同的概念,在求法上也有很大的差别,往往因为概念不清导致出错.4∶111.要注意概率P(A|B)与P(AB)的区别:
(1)在P(A|B)中,事件A,B发生有时间上的差异,B先A后;在P(AB)中,事件A,B同时发生.
(2)样本空间不同,在P(A|B)中,事件B成为样本空间;在P(AB)中,样本空间仍为Ω,因而有P(A|B)≥P(AB).12.求分布列,要检验概率的和是否为1,如果不是,要重新检查修正.还要注意识别独立重复试验和二项分布,然后用公式.[问题12] 若随机变量ξ的分布列如下表,则E(ξ)的
值为________.①P(μ-σ②P(μ-2σ③P(μ-3σA.0.6 B.0.4 C.0.3 D.0.2解析 ∵P(ξ<4)=0.8,∴P(ξ>4)=0.2,由题意知图象的对称轴为直线x=2,P(ξ<0)=P(ξ>4)=0.2,
∴P(0<ξ<4)=1-P(ξ<0)-P(ξ>4)=0.6.∴P(0<ξ<2)= P(0<ξ<4)=0.3.易错点1 统计图表识图不准致误易错点2 在几何概型中“测度”确定不准致误易错点3 分不清是排列还是组合致误易错警示易错点4 均匀分组与非均匀分组混淆致误易错点1 统计图表识图不准致误例1 如图所示是某公司(共有员工300人)2012年员工年薪情况的频率分布直方图,由此可知,员工中年薪在1.4万元~1.6万元之间的大约有________人.错解 由频率分布直方图,员工中年薪在1.4万元~1.6万元之间的频率为
1-(0.02+0.08+0.10+0.10+0.08)=0.62.
∴估计年薪在1.4万元~1.6万元之间约有
300×0.62=186(人).找准失分点本题主要混淆频率分布直方图与条形图纵轴的意义,
频率分布直方图中,纵轴(矩形高)表示“ ”,
每个小矩形的面积才表示落在该区间上的频率,由于概念不清,识图不准导致计算错误.正解 由所给图形可知,员工中年薪在1.4万元~1.6万元之间的频率为1-(0.02+0.08+0.08+0.10+0.10)×2=0.24.
所以员工中年薪在1.4万元~1.6万元之间的共有300×0.24=72(人).
答案 72易错点2 在几何概型中“测度”确定不准致误例2 如图所示,在等腰Rt△ABC中,
过直角顶点C在∠ACB内部任意作一条
射线CM,与线段AB交于点M,求AM<
AC的概率.错解 记AM那么对线段AD上的任意一点M都有AM即AM四个小岛,要建三座桥,将这四个岛连
接起来,不同的建桥方案共有多少种?错解 对于有一个中心的结构形式有 ,对于四个岛依次相连的形式有 ,∴共有2 =48(种).找准失分点没有分清是排列还是组合.正解 由题意可能有两种结构,如图:第一种: ,第二种: 易错点4 均匀分组与非均匀分组混淆致误例4 4个不同的小球放入编号为1、2、3、4的4个盒中,则恰有1个空盒的放法共有________种.(用数字作答)错解 288找准失分点正解 把4个球分成3组,每组至少1个,答案 144查缺补漏123456789101.在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.众数 B.平均数
C.中位数 D.标准差查缺补漏12345678910解析 对样本中每个数据都加上一个非零常数时不改变样本的方差和标准差,众数、中位数、平均数都发生改变.
答案 D查缺补漏123456789102.(2014·湖北)根据如下样本数据查缺补漏12345678910解析 作出散点图如右:答案 B查缺补漏12345678910查缺补漏12345678910解析 如图,平面区域Ω1就是三角形区
域OAB,平面区域Ω2与平面区域Ω1的重
叠部分就是区域OACD,答案 D查缺补漏123456789104.(2014·湖南)( x-2y)5的展开式中x2y3的系数是( )
A.-20 B.-5 C.5 D.20A查缺补漏123456789105. 如图,矩形ABCD中,点E为边CD上任
意一点,若在矩形ABCD内部随机取一个
点Q,则点Q取自△ABE内部的概率等于( )查缺补漏12345678910解析 这是一道几何概型的概率问题,点Q取自△ABE内部的概率为故选C.答案 C查缺补漏123456789106.(2014·福建)如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为________.查缺补漏12345678910解析 由题意知,所给图中两阴影部分面积相等,又该正方形面积为e2,故由几何概型的概率公式可得所求概率为 .查缺补漏123456789107.(2014·江西)10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率是________.查缺补漏123456789108.如图所示,图2中实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是 ,则此长方体的体积是________.查缺补漏12345678910解析 设长方体的高为h,由几何概型的概率计算公式可知,质点落在长方体的平面展开图内的概率解得h=3或h=- (舍去),故长方体的体积为1×1×3=3.答案 3查缺补漏123456789109.已知某人投篮的命中率为 ,则此人投篮4次,至少命中3次的概率是________.解析 该人投篮4次,命中3次的概率为查缺补漏12345678910查缺补漏1234567891010.某路段检查站监控录像显
示,在某时段内,有1 000辆
汽车通过该站,现在随机抽
取其中的200辆汽车进行车速
分析,分析的结果表示为如图所示的频率分布直方图,则估计在这一时段内通过该站的汽车中车速不小于90 km/h的约有________辆.(注:分析时车速均取整数)查缺补漏12345678910解析 由图可知,车速大于等于90 km/h的车辆未标出频率,而小于90 km/h的都标出了,故考虑对立事件.
由题图知车速小于90 km/h的汽车总数的频率之和为(0.01+0.02+0.04)×10=0.7,
所以车速不小于90 km/h的汽车总数的频率之和为
1-0.7=0.3.查缺补漏12345678910因此在这一时段内通过该站的车速不小于90 km/h的汽车有1 000×0.3=300(辆).
答案 300
概率与统计天津南开市2015届高三 概率与统计要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.随机抽样方法
简单随机抽样、系统抽样、分层抽样的共同点是抽样过程中每个个体被抽取的机会相等,且是不放回抽样.[问题1] 某社区现有480个住户,其中中等收入家庭200户、低收入家庭160户,其他为高收入家庭.在建设幸福社区的某次分层抽样调查中,高收入家庭被抽取了6户,则该社区本次抽取的总户数为________.242.对于统计图表问题,求解时,最重要的就是认真观察图表,从中提取有用信息和数据.对于频率分布直方图,应注意的是图中的每一个小矩形的面积是数据落在该区间上的频率.茎叶图没有原始数据信息的损失,但数据很大或有多组数据时,茎叶图就不那么直观、清晰了.[问题2] 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为________.203.众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数为频率分布直方图中最高矩形的底边中点的横坐标.
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
平均数:样本数据的算术平均数,即 (x1+x2+…+xn).
平均数等于频率分布直方图中每个小矩形的面积乘以小距形底边中点的横坐标之和.平均数等于频率分布直方图中每个小矩形的面积乘以小距形底边中点的横坐标之和.
标准差的平方就是方差,方差的计算[问题3] 已知一个样本中的数据为0.12,0.15,0.13,0.15,0.14,0.17,0.15,0.16,0.13,0.14,则该样本的众数、中位数分别是____________.0.15、0.1455.独立性检验的基本方法
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表如表:根据观测数据计算由公式k=
所给出的检验随机变量K2的观测值k,并且k的值越大,说明“X与Y有关系”成立的可能性越大,可以利用数据来确定“X与Y有关系”的可信程度.[问题5] 为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:则至少有________的把握认为喜爱打篮球与性别有关.(请用百分数表示)99.5%6.互斥事件有一个发生的概率P(A+B)=P(A)+P(B)
(1)公式适合范围:事件A与B互斥.
(2)P( )=1-P(A).7.古典概型
P(A)= (其中,n为一次试验中可能出现的结果总数,m为事件A在试验中包含的基本事件个数)[问题7] 若将一枚质地均匀的骰子先后抛掷2次,则出现向上的点数之和为4的概率为________.[问题8] 在棱长为2的正方体ABCD—A1B1C1D1中,点O为底面ABCD的中心,在正方体ABCD—A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为( )解析 记“点P到点O的距离大于1”为A,答案 B9.解排列、组合问题的依据是:分类相加,分步相乘,有序排列,无序组合.
解排列、组合问题的规律是:相邻问题捆绑法;不相邻问题插空法;多排问题单排法;定位问题优先法;定序问题倍缩法;多元问题分类法;有序分配分步法;综合问题先选后排法;至多至少问题间接法.[问题9] (1)将5封信投入3个邮筒,不同的投法共有________种.
(2)从4台甲型和5台乙型电视机中任意取出3台,其中至少要甲型和乙型电视机各一台,则不同的取法共有________种.70特别提醒:二项式系数最大项与展开式系数最大项是两个不同的概念,在求法上也有很大的差别,往往因为概念不清导致出错.4∶111.要注意概率P(A|B)与P(AB)的区别:
(1)在P(A|B)中,事件A,B发生有时间上的差异,B先A后;在P(AB)中,事件A,B同时发生.
(2)样本空间不同,在P(A|B)中,事件B成为样本空间;在P(AB)中,样本空间仍为Ω,因而有P(A|B)≥P(AB).12.求分布列,要检验概率的和是否为1,如果不是,要重新检查修正.还要注意识别独立重复试验和二项分布,然后用公式.[问题12] 若随机变量ξ的分布列如下表,则E(ξ)的
值为________.①P(μ-σ
∴P(0<ξ<4)=1-P(ξ<0)-P(ξ>4)=0.6.∴P(0<ξ<2)= P(0<ξ<4)=0.3.易错点1 统计图表识图不准致误易错点2 在几何概型中“测度”确定不准致误易错点3 分不清是排列还是组合致误易错警示易错点4 均匀分组与非均匀分组混淆致误易错点1 统计图表识图不准致误例1 如图所示是某公司(共有员工300人)2012年员工年薪情况的频率分布直方图,由此可知,员工中年薪在1.4万元~1.6万元之间的大约有________人.错解 由频率分布直方图,员工中年薪在1.4万元~1.6万元之间的频率为
1-(0.02+0.08+0.10+0.10+0.08)=0.62.
∴估计年薪在1.4万元~1.6万元之间约有
300×0.62=186(人).找准失分点本题主要混淆频率分布直方图与条形图纵轴的意义,
频率分布直方图中,纵轴(矩形高)表示“ ”,
每个小矩形的面积才表示落在该区间上的频率,由于概念不清,识图不准导致计算错误.正解 由所给图形可知,员工中年薪在1.4万元~1.6万元之间的频率为1-(0.02+0.08+0.08+0.10+0.10)×2=0.24.
所以员工中年薪在1.4万元~1.6万元之间的共有300×0.24=72(人).
答案 72易错点2 在几何概型中“测度”确定不准致误例2 如图所示,在等腰Rt△ABC中,
过直角顶点C在∠ACB内部任意作一条
射线CM,与线段AB交于点M,求AM<
AC的概率.错解 记AM
接起来,不同的建桥方案共有多少种?错解 对于有一个中心的结构形式有 ,对于四个岛依次相连的形式有 ,∴共有2 =48(种).找准失分点没有分清是排列还是组合.正解 由题意可能有两种结构,如图:第一种: ,第二种: 易错点4 均匀分组与非均匀分组混淆致误例4 4个不同的小球放入编号为1、2、3、4的4个盒中,则恰有1个空盒的放法共有________种.(用数字作答)错解 288找准失分点正解 把4个球分成3组,每组至少1个,答案 144查缺补漏123456789101.在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.众数 B.平均数
C.中位数 D.标准差查缺补漏12345678910解析 对样本中每个数据都加上一个非零常数时不改变样本的方差和标准差,众数、中位数、平均数都发生改变.
答案 D查缺补漏123456789102.(2014·湖北)根据如下样本数据查缺补漏12345678910解析 作出散点图如右:答案 B查缺补漏12345678910查缺补漏12345678910解析 如图,平面区域Ω1就是三角形区
域OAB,平面区域Ω2与平面区域Ω1的重
叠部分就是区域OACD,答案 D查缺补漏123456789104.(2014·湖南)( x-2y)5的展开式中x2y3的系数是( )
A.-20 B.-5 C.5 D.20A查缺补漏123456789105. 如图,矩形ABCD中,点E为边CD上任
意一点,若在矩形ABCD内部随机取一个
点Q,则点Q取自△ABE内部的概率等于( )查缺补漏12345678910解析 这是一道几何概型的概率问题,点Q取自△ABE内部的概率为故选C.答案 C查缺补漏123456789106.(2014·福建)如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为________.查缺补漏12345678910解析 由题意知,所给图中两阴影部分面积相等,又该正方形面积为e2,故由几何概型的概率公式可得所求概率为 .查缺补漏123456789107.(2014·江西)10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率是________.查缺补漏123456789108.如图所示,图2中实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是 ,则此长方体的体积是________.查缺补漏12345678910解析 设长方体的高为h,由几何概型的概率计算公式可知,质点落在长方体的平面展开图内的概率解得h=3或h=- (舍去),故长方体的体积为1×1×3=3.答案 3查缺补漏123456789109.已知某人投篮的命中率为 ,则此人投篮4次,至少命中3次的概率是________.解析 该人投篮4次,命中3次的概率为查缺补漏12345678910查缺补漏1234567891010.某路段检查站监控录像显
示,在某时段内,有1 000辆
汽车通过该站,现在随机抽
取其中的200辆汽车进行车速
分析,分析的结果表示为如图所示的频率分布直方图,则估计在这一时段内通过该站的汽车中车速不小于90 km/h的约有________辆.(注:分析时车速均取整数)查缺补漏12345678910解析 由图可知,车速大于等于90 km/h的车辆未标出频率,而小于90 km/h的都标出了,故考虑对立事件.
由题图知车速小于90 km/h的汽车总数的频率之和为(0.01+0.02+0.04)×10=0.7,
所以车速不小于90 km/h的汽车总数的频率之和为
1-0.7=0.3.查缺补漏12345678910因此在这一时段内通过该站的车速不小于90 km/h的汽车有1 000×0.3=300(辆).
答案 300
同课章节目录
