【高考专辑】【专题15】2015年高三数学(理)【押题精练】推理与证明
文档属性
| 名称 | 【高考专辑】【专题15】2015年高三数学(理)【押题精练】推理与证明 |  | |
| 格式 | zip | ||
| 文件大小 | 603.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 18:40:25 | ||
图片预览










文档简介
课件66张PPT。专题15
推理与证明推理与证明主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.合情推理
(1)归纳推理
①归纳推理是由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理.
②归纳推理的思维过程如下:实验、观察概括、推广猜测一般性结论→→(2)类比推理
①类比推理是由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理.
②类比推理的思维过程如下:观察、比较联想、类推猜测新的结论→→2.演绎推理
(1)“三段论”是演绎推理的一般模式,包括:
①大前提——已知的一般原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.(2)合情推理与演绎推理的区别
归纳和类比是常用的合情推理,从推理形式上看,归纳是由部分到整体、个别到一般的推理;类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理.从推理所得的结论来看,合情推理的结论不一定正确,有待进一步证明;演绎推理在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确.3.直接证明
(1)综合法
用P表示已知条件、已有的定义、定理、公理等,Q表示所要证明的结论,则综合法可用框图表示为:P?Q1Q1?Q2Q2?Q3Qn?Q→→→…→(2)分析法
用Q表示要证明的结论,则分析法可用框图表示为:Q?P1P1?P2P2?P3得到一个明显
成立的条件→→→…→4.间接证明
反证法的证明过程可以概括为“否定——推理——否定”,即从否定结论开始,经过正确的推理,导致逻辑矛盾,从而达到新的否定(即肯定原命题)的过程.用反证法证明命题“若p,则q”的过程可以用如图所示的框图表示.肯定条件p
否定结论q导致逻
辑矛盾“既p,又綈q”
为假“若p,则q”
为真→→→5.数学归纳法
数学归纳法证明的步骤:
(1)证明当n取第一个值n0(n0∈N*)时命题成立.
(2)假设n=k(k∈N*,且k≥n0)时命题成立,证明n=k+1时命题也成立.
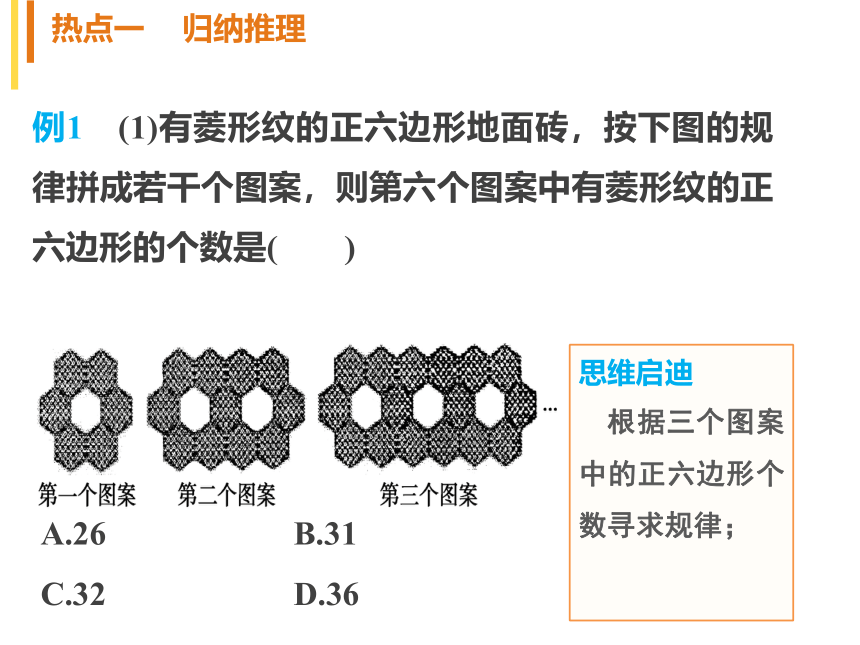
由(1)(2)可知,对任意n≥n0,且n∈N*时,命题都成立.热点一 归纳推理热点二 类比推理热点三 直接证明和间接证明热点分类突破热点四 数学归纳法例1 (1)有菱形纹的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )热点一 归纳推理思维启迪
根据三个图案中的正六边形个数寻求规律;A.26 B.31
C.32 D.36解析 有菱形纹的正六边形个数如下表:由表可以看出有菱形纹的正六边形的个数依次组成一个以6为首项,以5为公差的等差数列,
所以第六个图案中有菱形纹的正六边形的个数是6+5×(6-1)=31.故选B.
答案 B(2)两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位的排法如图所示,则下列座位号码符合要求的应当是( )A.48,49 B.62,63
C.75,76 D.84,85思维启迪
靠窗口的座位号码能被5整除或者被5除余1.解析 由已知图形中座位的排列顺序,可得:
被5除余1的数和能被5整除的座位号临窗,
由于两旅客希望座位连在一起,且有一个靠窗,
分析答案中的4组座位号,只有D符合条件.
答案 D变式训练1(1)四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第202次互换座位后,小兔坐在第______号座位上.A.1 B.2 C.3 D.4解析 考虑小兔所坐的座位号,第一次坐在1号位上,第二次坐在2号位上,第三次坐在4号位上,第四次坐在3号位上,第五次坐在1号位上,
因此小兔的座位数更换次数以4为周期,
因为202=50×4+2,因此第202次互换后,小兔所在的座位号与小兔第二次互换座位号所在的座位号相同,
因此小兔坐在2号位上,故选B.
答案 B热点二 类比推理思维启迪
平面几何中的面积可类比到空间几何中的体积;解析 平面几何中,圆的面积与圆的半径的平方成正比,
而在空间几何中,球的体积与半径的立方成正比,所以=思维启迪
可利用和角或差角公式猜想,然后验证.故知ch(x+y)=chx chy+shx shy,
或sh(x-y)=shx chy-chx shy,
或sh(x+y)=shx chy+chx shy.
答案 ch(x-y)=chx chy-shx shy变式训练2 解析 由{an}为等差数列,设公差为d,又正项数列{cn}为等比数列,设公比为q,答案 D解析 设A(x1,y1),B(x2,y2),M(x0,y0),热点三 直接证明和间接证明(1)求数列{an},{bn}的通项公式;思维启迪
利用已知递推式中的特点构造数列{1- };由anan+1<0,知数列{an}的项正负相间出现,(2)证明:数列{bn}中的任意三项不可能成等差数列.思维启迪
否定性结论的证明可用反证法.证明 假设存在某三项成等差数列,不妨设为bm、bn、bp,
其中m、n、p是互不相等的正整数,可设m 利用{an}的前n项确定通项公式(公差、首项),{bn}的通项公式可分段给出;(1)求an,bn;解得a1=2,d=4,所以an=4n-2.思维启迪
先求Tn,归纳猜想Tn与2n2+ 的关系,再用数学归纳法证明.解 T2n=1+2×2-3+22+2×4-3+24+…+22n-2+2×2n-3=1+22+24+…+22n-2+4(1+2+…+n)-3n即n≥2时,4n>4n+1.下面用数学归纳法证明:
①当n=2时,42=16,4×2+1=9,16>9,成立;
②假设当n=k(k≥2)时成立,即4k>4k+1.
则当n=k+1时,4k+1=4·4k>4·(4k+1)
=16k+4>4k+5=4(k+1)+1,
所以n=k+1时成立.由①②得,当n≥2时,4n>4n+1成立.变式训练4 (1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;解 当n=1时,f(1)=1,g(1)=1,所以f(1)=g(1),(2)猜想f(n)与g(n)的大小关系,并给出证明.解 由(1),猜想f(n)≤g(n),下面用数学归纳法给出证明
①当n=1,2,3时,不等式显然成立
②假设当n=k(k≥3)时不等式成立,那么,当n=k+1时,即当n=k+1时,不等式成立.
由①②可知,对一切n∈N*,都有f(n)≤g(n)成立.1.合情推理的精髓是“合情”,即得到的结论符合“情理”,其中主要是归纳推理与类比推理.归纳推理是由部分得到整体的一种推理模式.类比推理是由此及彼的推理模式;演绎推理是一种严格的证明方式.
2.直接证明的最基本的两种证明方法是综合法和分析法,这两种方法也是解决数学问题时常见的思维方式.在实际解题时,通常先用分析法寻求解题思路,再用综合法有条理地表述解题过程.本讲规律总结3.数学归纳法是证明与正整数有关的数学命题的一种方法,在遇到与正整数有关的数学命题时,要考虑是否可以使用数学归纳法进行证明.
(1)在证明过程中突出两个“凑”字,即一“凑”假设,二“凑”结论,关键是在证明n=k+1时要用上n=k时的假设,其次要明确n=k+1时证明的目标,充分考虑由n=k到n=k+1时,命题形式之间的区别和联系,化异为同,中间的计算过程千万不能省略.
(2)注意“两个步骤、一个结论”一个也不能少,切忌忘记归纳结论.真题感悟押题精练真题与押题12真题感悟1.(2014·福建)若集合{a,b,c,d}={1,2,3,4},且下列四个关系:
①a=1;②b≠1;③c=2;④d≠4.有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是________.12真题感悟解析 由题意知①②③④中有且只有一个正确,其余三个均不正确,下面分类讨论满足条件的有序数组(a,b,c,d)的个数:
(1)若①正确,即a=1,则②③④都错误,即b=1,c≠2,d=4.其中a=1与b=1矛盾,显然此种情况不存在;12真题感悟(2)若②正确,即b≠1,则①③④都错误,即a≠1,c≠2,d=4,则当b=2时,有a=3,c=1;当b=3时,有a=2,c=1,此时有2种有序数组.
(3)若③正确,即c=2,则①②④都错误,即a≠1,b=1,d=4,则a=3,即此种情况有1种有序数组.12真题感悟(4)若④正确,即d≠4,则①②③都错误,即a≠1,b=1,c≠2,则当d=2时,有a=3,c=4或a=4,c=3,有2种有序数组;当d=3时,有c=4,a=2,仅1种有序数组.
综上可得,共有2+1+2+1=6(种)有序数组.
答案 6真题感悟212.(2014·陕西)观察分析下表中的数据:猜想一般凸多面体中F,V,E所满足的等式是____________.解析 观察F,V,E的变化得F+V-E=2.F+V-E=2押题精练121.圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则n个点连成的弦最多可把圆面分成________部分.( )
A.2n-1 B.2n
C.2n+1 D.2n+2押题精练12解析 由已知条件得:押题精练12由此可以归纳出,当点数为n时,连成的弦数为 ;弦把圆面分成的部分数为2n-1,故选A.
答案 A押题精练12押题精练12相加,得1×2+2×3+…+n(n+1)
= n(n+1)(n+2).
类比上述方法,计算“1×2×3+2×3×4+…+n(n+1)(n+2)”的结果为____________.押题精练12解析 类比k(k+1)= [k(k+1)(k+2)-(k-1)k(k+1)],可得到k(k+1)(k+2)= [k(k+1)(k+2)(k+3)-(k-1)
k(k+1)(k+2)],先逐项裂项,然后累加即得 n(n+1)(n+2)(n+3).答案 n(n+1)(n+2)(n+3)
推理与证明推理与证明主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.合情推理
(1)归纳推理
①归纳推理是由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理.
②归纳推理的思维过程如下:实验、观察概括、推广猜测一般性结论→→(2)类比推理
①类比推理是由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理.
②类比推理的思维过程如下:观察、比较联想、类推猜测新的结论→→2.演绎推理
(1)“三段论”是演绎推理的一般模式,包括:
①大前提——已知的一般原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.(2)合情推理与演绎推理的区别
归纳和类比是常用的合情推理,从推理形式上看,归纳是由部分到整体、个别到一般的推理;类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理.从推理所得的结论来看,合情推理的结论不一定正确,有待进一步证明;演绎推理在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确.3.直接证明
(1)综合法
用P表示已知条件、已有的定义、定理、公理等,Q表示所要证明的结论,则综合法可用框图表示为:P?Q1Q1?Q2Q2?Q3Qn?Q→→→…→(2)分析法
用Q表示要证明的结论,则分析法可用框图表示为:Q?P1P1?P2P2?P3得到一个明显
成立的条件→→→…→4.间接证明
反证法的证明过程可以概括为“否定——推理——否定”,即从否定结论开始,经过正确的推理,导致逻辑矛盾,从而达到新的否定(即肯定原命题)的过程.用反证法证明命题“若p,则q”的过程可以用如图所示的框图表示.肯定条件p
否定结论q导致逻
辑矛盾“既p,又綈q”
为假“若p,则q”
为真→→→5.数学归纳法
数学归纳法证明的步骤:
(1)证明当n取第一个值n0(n0∈N*)时命题成立.
(2)假设n=k(k∈N*,且k≥n0)时命题成立,证明n=k+1时命题也成立.
由(1)(2)可知,对任意n≥n0,且n∈N*时,命题都成立.热点一 归纳推理热点二 类比推理热点三 直接证明和间接证明热点分类突破热点四 数学归纳法例1 (1)有菱形纹的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )热点一 归纳推理思维启迪
根据三个图案中的正六边形个数寻求规律;A.26 B.31
C.32 D.36解析 有菱形纹的正六边形个数如下表:由表可以看出有菱形纹的正六边形的个数依次组成一个以6为首项,以5为公差的等差数列,
所以第六个图案中有菱形纹的正六边形的个数是6+5×(6-1)=31.故选B.
答案 B(2)两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位的排法如图所示,则下列座位号码符合要求的应当是( )A.48,49 B.62,63
C.75,76 D.84,85思维启迪
靠窗口的座位号码能被5整除或者被5除余1.解析 由已知图形中座位的排列顺序,可得:
被5除余1的数和能被5整除的座位号临窗,
由于两旅客希望座位连在一起,且有一个靠窗,
分析答案中的4组座位号,只有D符合条件.
答案 D变式训练1(1)四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第202次互换座位后,小兔坐在第______号座位上.A.1 B.2 C.3 D.4解析 考虑小兔所坐的座位号,第一次坐在1号位上,第二次坐在2号位上,第三次坐在4号位上,第四次坐在3号位上,第五次坐在1号位上,
因此小兔的座位数更换次数以4为周期,
因为202=50×4+2,因此第202次互换后,小兔所在的座位号与小兔第二次互换座位号所在的座位号相同,
因此小兔坐在2号位上,故选B.
答案 B热点二 类比推理思维启迪
平面几何中的面积可类比到空间几何中的体积;解析 平面几何中,圆的面积与圆的半径的平方成正比,
而在空间几何中,球的体积与半径的立方成正比,所以=思维启迪
可利用和角或差角公式猜想,然后验证.故知ch(x+y)=chx chy+shx shy,
或sh(x-y)=shx chy-chx shy,
或sh(x+y)=shx chy+chx shy.
答案 ch(x-y)=chx chy-shx shy变式训练2 解析 由{an}为等差数列,设公差为d,又正项数列{cn}为等比数列,设公比为q,答案 D解析 设A(x1,y1),B(x2,y2),M(x0,y0),热点三 直接证明和间接证明(1)求数列{an},{bn}的通项公式;思维启迪
利用已知递推式中的特点构造数列{1- };由anan+1<0,知数列{an}的项正负相间出现,(2)证明:数列{bn}中的任意三项不可能成等差数列.思维启迪
否定性结论的证明可用反证法.证明 假设存在某三项成等差数列,不妨设为bm、bn、bp,
其中m、n、p是互不相等的正整数,可设m
先求Tn,归纳猜想Tn与2n2+ 的关系,再用数学归纳法证明.解 T2n=1+2×2-3+22+2×4-3+24+…+22n-2+2×2n-3=1+22+24+…+22n-2+4(1+2+…+n)-3n即n≥2时,4n>4n+1.下面用数学归纳法证明:
①当n=2时,42=16,4×2+1=9,16>9,成立;
②假设当n=k(k≥2)时成立,即4k>4k+1.
则当n=k+1时,4k+1=4·4k>4·(4k+1)
=16k+4>4k+5=4(k+1)+1,
所以n=k+1时成立.由①②得,当n≥2时,4n>4n+1成立.变式训练4 (1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;解 当n=1时,f(1)=1,g(1)=1,所以f(1)=g(1),(2)猜想f(n)与g(n)的大小关系,并给出证明.解 由(1),猜想f(n)≤g(n),下面用数学归纳法给出证明
①当n=1,2,3时,不等式显然成立
②假设当n=k(k≥3)时不等式成立,那么,当n=k+1时,即当n=k+1时,不等式成立.
由①②可知,对一切n∈N*,都有f(n)≤g(n)成立.1.合情推理的精髓是“合情”,即得到的结论符合“情理”,其中主要是归纳推理与类比推理.归纳推理是由部分得到整体的一种推理模式.类比推理是由此及彼的推理模式;演绎推理是一种严格的证明方式.
2.直接证明的最基本的两种证明方法是综合法和分析法,这两种方法也是解决数学问题时常见的思维方式.在实际解题时,通常先用分析法寻求解题思路,再用综合法有条理地表述解题过程.本讲规律总结3.数学归纳法是证明与正整数有关的数学命题的一种方法,在遇到与正整数有关的数学命题时,要考虑是否可以使用数学归纳法进行证明.
(1)在证明过程中突出两个“凑”字,即一“凑”假设,二“凑”结论,关键是在证明n=k+1时要用上n=k时的假设,其次要明确n=k+1时证明的目标,充分考虑由n=k到n=k+1时,命题形式之间的区别和联系,化异为同,中间的计算过程千万不能省略.
(2)注意“两个步骤、一个结论”一个也不能少,切忌忘记归纳结论.真题感悟押题精练真题与押题12真题感悟1.(2014·福建)若集合{a,b,c,d}={1,2,3,4},且下列四个关系:
①a=1;②b≠1;③c=2;④d≠4.有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是________.12真题感悟解析 由题意知①②③④中有且只有一个正确,其余三个均不正确,下面分类讨论满足条件的有序数组(a,b,c,d)的个数:
(1)若①正确,即a=1,则②③④都错误,即b=1,c≠2,d=4.其中a=1与b=1矛盾,显然此种情况不存在;12真题感悟(2)若②正确,即b≠1,则①③④都错误,即a≠1,c≠2,d=4,则当b=2时,有a=3,c=1;当b=3时,有a=2,c=1,此时有2种有序数组.
(3)若③正确,即c=2,则①②④都错误,即a≠1,b=1,d=4,则a=3,即此种情况有1种有序数组.12真题感悟(4)若④正确,即d≠4,则①②③都错误,即a≠1,b=1,c≠2,则当d=2时,有a=3,c=4或a=4,c=3,有2种有序数组;当d=3时,有c=4,a=2,仅1种有序数组.
综上可得,共有2+1+2+1=6(种)有序数组.
答案 6真题感悟212.(2014·陕西)观察分析下表中的数据:猜想一般凸多面体中F,V,E所满足的等式是____________.解析 观察F,V,E的变化得F+V-E=2.F+V-E=2押题精练121.圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则n个点连成的弦最多可把圆面分成________部分.( )
A.2n-1 B.2n
C.2n+1 D.2n+2押题精练12解析 由已知条件得:押题精练12由此可以归纳出,当点数为n时,连成的弦数为 ;弦把圆面分成的部分数为2n-1,故选A.
答案 A押题精练12押题精练12相加,得1×2+2×3+…+n(n+1)
= n(n+1)(n+2).
类比上述方法,计算“1×2×3+2×3×4+…+n(n+1)(n+2)”的结果为____________.押题精练12解析 类比k(k+1)= [k(k+1)(k+2)-(k-1)k(k+1)],可得到k(k+1)(k+2)= [k(k+1)(k+2)(k+3)-(k-1)
k(k+1)(k+2)],先逐项裂项,然后累加即得 n(n+1)(n+2)(n+3).答案 n(n+1)(n+2)(n+3)
同课章节目录
