【高考专辑】【专题20】2015年高三数学(理)【押题精练】函数的应用
文档属性
| 名称 | 【高考专辑】【专题20】2015年高三数学(理)【押题精练】函数的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 18:49:16 | ||
图片预览










文档简介
课件53张PPT。专题20
函数的应用函数的应用主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.函数的零点与方程的根
(1)函数的零点
对于函数f(x),我们把使f(x)=0的实数x叫做函数f(x)的零点.
(2)函数的零点与方程根的关系
函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.(3)零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b)使得f(c)=0,这个c也就是方程f(x)=0的根.
注意以下两点:
①满足条件的零点可能不唯一;
②不满足条件时,也可能有零点.
(4)二分法求函数零点的近似值,二分法求方程的近似解.2.函数模型
解决函数模型的实际应用题,首先考虑题目考查的函数模型,并要注意定义域.其解题步骤是(1)阅读理解,审清题意:分析出已知什么,求什么,从中提炼出相应的数学问题;(2)数学建模:弄清题目中的已知条件和数量关系,建立函数关系式;(3)解函数模型:利用数学方法得出函数模型的数学结果;(4)实际问题作答:将数学问题的结果转化成实际问题作出解答.热点一 函数的零点热点二 函数的零点与参数的范围热点三 函数的实际应用问题热点分类突破例1 (1)函数f(x)=ln(x+1)- 的零点所在的区间是( )
A.( ,1) B.(1,e-1)
C.(e-1,2) D.(2,e)热点一 函数的零点思维启迪
根据二分法原理,逐个判断;解析 因为f( )=ln -4<0,f(1)=ln 2-2<0,f(e-1)=1- <0,f(2)=ln 3-1>0,故零点在区间(e-1,2)内.
答案 C思维启迪
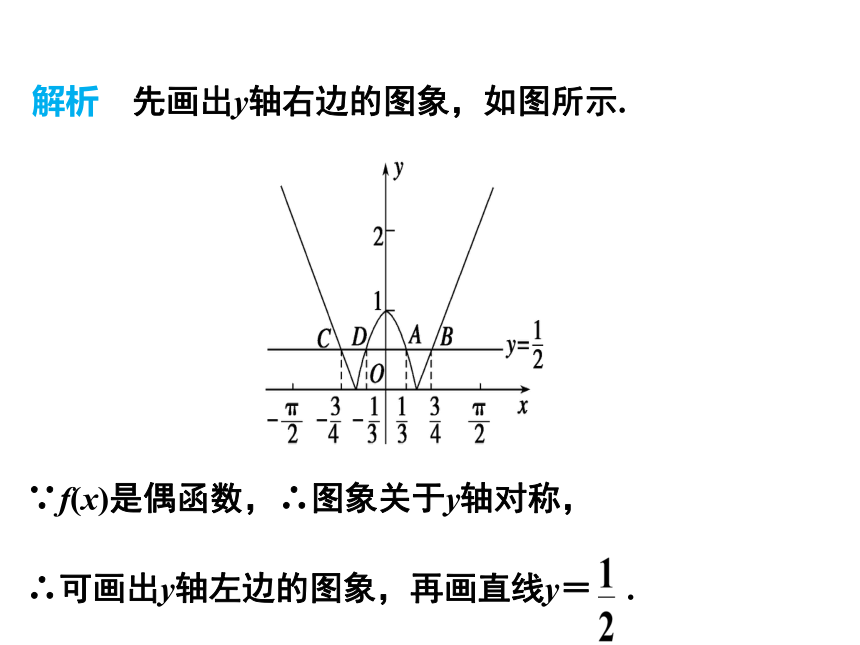
画出函数图象,利用数形结合思想解决.解析 先画出y轴右边的图象,如图所示.∵f(x)是偶函数,∴图象关于y轴对称,∴可画出y轴左边的图象,再画直线y= .设与曲线交于点A,B,C,D,先分别求出A,B两点的横坐标.答案 A变式训练1(1)已知函数f(x)=( )x-cos x,则f(x)在[0,2π]上的零点个数是( )
A.1 B.2 C.3 D.4解析 f(x)在[0,2π]上的零点个数就是函数y=( )x和y=cos x的图象在[0,2π]上的交点个数,而函数y=( )x和y=cos x的图象在[0,2π]上的交点有3个,故选C.C(2)已知a是函数f(x)=2x-log x的零点,若0A.f(x0)=0 B.f(x0)>0
C.f(x0)<0 D.f(x0)的符号不确定解析 ∵f(x)=2x-log x在(0,+∞)上是增函数,又a是函数f(x)=2x-log x的零点,即f(a)=0,∴当0 设f(x)=(x2-1)?(4+x),若函数y=
f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是( )
A.(-2,1) B.[0,1]
C.[-2,0) D.[-2,1)热点二 函数的零点与参数的范围思维启迪
先确定函数f(x)的解析式,再利用数形结合思想求k的范围.解析 解不等式:x2-1-(4+x)≥1,
得:x≤-2或x≥3,函数y=f(x)+k的图象与x轴恰有三个不同交点转化为函数y=f(x)的图象和直线y=-k恰有三个不同交点.如图,所以-1<-k≤2,故-2≤k<1.答案 D变式训练2 定义在R上的函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),若方程3a(f(x))2+2bf(x)+c=0恰有6个不同的实根,则实数a的取值范围是________.解析 ∵函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),∴-1和1是f′(x)=0的根,
∵f′(x)=3ax2+2bx+c,∴f(x)=ax3-3ax,
∵3a(f(x))2+2bf(x)+c=0,
∴3a(f(x))2-3a=0,∴f2(x)=1,∴f(x)=±1,例3 省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f(x)=| -a|+2a+ ,x∈[0,24],其中a是与气象有关的参数,且a∈[0, ],若用每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).热点三 函数的实际应用问题(1)令t= ,x∈[0,24],求t的取值范围;思维启迪
分x=0和x≠0两种情况,当x≠0时变形使用基本不等式求解.解 当x=0时,t=0;当0 利用换元法把函数f(x)转化成g(t)=|t-a|+2a+ ,再把函数g(t)写成分段函数后求M(a).∵g(t)在[0,a]上单调递减,在(a, ]上单调递增,∴当且仅当0≤a≤ 时,M(a)≤2.变式训练3已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的
销售收入为R(x)万元,且R(x)=(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;解 当010时,W=xR(x)-(10+2.7x)=98- -2.7x.(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大?(注:年利润=年销售收入-年总成本)解 ①当00;当x∈(9,10)时,W′<0,∴当x=9时,W取得最大值,且Wmax=8.1×9- ·93-10=38.6.②当x>10时,综合①②知:当x=9时,W取最大值38.6万元,
故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.本讲规律总结1.函数与方程
(1)函数f(x)有零点?方程f(x)=0有根?函数f(x)的图象与x轴有交点.
(2)函数f(x)的零点存在性定理
如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且有f(a)·f(b)<0,那么,函数f(x)在区间(a,b)内有零点,即存在c∈(a,b),使f(c)=0.①如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且函数f(x)在区间[a,b]上是一个单调函数,那么当f(a)·f(b)<0时,函数f(x)在区间(a,b)内有唯一的零点,即存在唯一的c∈(a,b),使f(c)=0.
②如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且有f(a)·f(b)>0,那么,函数f(x)在区间(a,b)内不一定没有零点.2.函数综合题的求解往往应用多种知识和技能.因此,必须全面掌握有关的函数知识,并且严谨审题,弄清题目的已知条件,尤其要挖掘题目中的隐含条件.要认真分析,处理好各种关系,把握问题的主线,运用相关的知识和方法逐步化归为基本问题来解决.真题感悟押题精练真题与押题12真题感悟12真题感悟解析 作出函数f(x)的图象如图所示,其中A(1,1),B(0,-2).12真题感悟因为直线y=mx+m=m(x+1)恒过定点C(-1,0),故当直线y=m(x+1)在AC位置时,m= ,可知当直线y=m(x+1)在x轴和AC之间运动时两图象有两个不同的交点(直线y=m(x+1)可与AC重合但不能与x轴重合),此时0粒数占加工总粒数的百分比称为“可食用
率”.在特定条件下,可食用率p与加工时
间t(单位:分钟)满足函数关系p=at2+bt+
c(a、b、c是常数),如图记录了三次实验的
数据.根据上述函数模型和实验数据,可以
得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟真题感悟21解析 根据图表,把(t,p)的三组数据(3,0.7),(4,0.8),(5,0.5)分别代入函数关系式,真题感悟21即最佳加工时间为3.75分钟.
答案 B押题精练123解析 当f(x)=0时,x=-1或x=1,
故f[f(x)+1]=0时,f(x)+1=-1或1.当f(x)+1=-1,即f(x)=-2时,解得x=-3或x= ;押题精练123当f(x)+1=1,即f(x)=0时,解得x=-1或x=1.
故函数y=f[f(x)+1]有四个不同的零点.
答案 4押题精练1232.函数f(x)=xex-a有两个零点,则实数a的取值范围是________.解析 令f′(x)=(x+1)ex=0,得x=-1,
则当x∈(-∞,-1)时,f′(x)<0,
当x∈(-1,+∞)时,f′(x)>0,
f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,押题精练123要使f(x)有两个零点,则极小值f(-1)<0,即-e-1-a<0,∴a>- ,又x→-∞时,f(x)>0,则a<0,∴a∈(- ,0).答案 (- ,0)押题精练1233.某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*).则当每台机器运转________年时,年平均利润最大,最大值是________万元.押题精练123解析 由题意知每台机器运转x年的年平均利润为
=18-(x+ ),而x>0,故 ≤18-2 =8,当且仅当x=5时,年平均利润最大,最大值为8万元.
答案 5 8
函数的应用函数的应用主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.函数的零点与方程的根
(1)函数的零点
对于函数f(x),我们把使f(x)=0的实数x叫做函数f(x)的零点.
(2)函数的零点与方程根的关系
函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.(3)零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b)使得f(c)=0,这个c也就是方程f(x)=0的根.
注意以下两点:
①满足条件的零点可能不唯一;
②不满足条件时,也可能有零点.
(4)二分法求函数零点的近似值,二分法求方程的近似解.2.函数模型
解决函数模型的实际应用题,首先考虑题目考查的函数模型,并要注意定义域.其解题步骤是(1)阅读理解,审清题意:分析出已知什么,求什么,从中提炼出相应的数学问题;(2)数学建模:弄清题目中的已知条件和数量关系,建立函数关系式;(3)解函数模型:利用数学方法得出函数模型的数学结果;(4)实际问题作答:将数学问题的结果转化成实际问题作出解答.热点一 函数的零点热点二 函数的零点与参数的范围热点三 函数的实际应用问题热点分类突破例1 (1)函数f(x)=ln(x+1)- 的零点所在的区间是( )
A.( ,1) B.(1,e-1)
C.(e-1,2) D.(2,e)热点一 函数的零点思维启迪
根据二分法原理,逐个判断;解析 因为f( )=ln -4<0,f(1)=ln 2-2<0,f(e-1)=1- <0,f(2)=ln 3-1>0,故零点在区间(e-1,2)内.
答案 C思维启迪
画出函数图象,利用数形结合思想解决.解析 先画出y轴右边的图象,如图所示.∵f(x)是偶函数,∴图象关于y轴对称,∴可画出y轴左边的图象,再画直线y= .设与曲线交于点A,B,C,D,先分别求出A,B两点的横坐标.答案 A变式训练1(1)已知函数f(x)=( )x-cos x,则f(x)在[0,2π]上的零点个数是( )
A.1 B.2 C.3 D.4解析 f(x)在[0,2π]上的零点个数就是函数y=( )x和y=cos x的图象在[0,2π]上的交点个数,而函数y=( )x和y=cos x的图象在[0,2π]上的交点有3个,故选C.C(2)已知a是函数f(x)=2x-log x的零点,若0
C.f(x0)<0 D.f(x0)的符号不确定解析 ∵f(x)=2x-log x在(0,+∞)上是增函数,又a是函数f(x)=2x-log x的零点,即f(a)=0,∴当0
f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是( )
A.(-2,1) B.[0,1]
C.[-2,0) D.[-2,1)热点二 函数的零点与参数的范围思维启迪
先确定函数f(x)的解析式,再利用数形结合思想求k的范围.解析 解不等式:x2-1-(4+x)≥1,
得:x≤-2或x≥3,函数y=f(x)+k的图象与x轴恰有三个不同交点转化为函数y=f(x)的图象和直线y=-k恰有三个不同交点.如图,所以-1<-k≤2,故-2≤k<1.答案 D变式训练2 定义在R上的函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),若方程3a(f(x))2+2bf(x)+c=0恰有6个不同的实根,则实数a的取值范围是________.解析 ∵函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),∴-1和1是f′(x)=0的根,
∵f′(x)=3ax2+2bx+c,∴f(x)=ax3-3ax,
∵3a(f(x))2+2bf(x)+c=0,
∴3a(f(x))2-3a=0,∴f2(x)=1,∴f(x)=±1,例3 省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f(x)=| -a|+2a+ ,x∈[0,24],其中a是与气象有关的参数,且a∈[0, ],若用每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).热点三 函数的实际应用问题(1)令t= ,x∈[0,24],求t的取值范围;思维启迪
分x=0和x≠0两种情况,当x≠0时变形使用基本不等式求解.解 当x=0时,t=0;当0
销售收入为R(x)万元,且R(x)=(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;解 当0
故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.本讲规律总结1.函数与方程
(1)函数f(x)有零点?方程f(x)=0有根?函数f(x)的图象与x轴有交点.
(2)函数f(x)的零点存在性定理
如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且有f(a)·f(b)<0,那么,函数f(x)在区间(a,b)内有零点,即存在c∈(a,b),使f(c)=0.①如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且函数f(x)在区间[a,b]上是一个单调函数,那么当f(a)·f(b)<0时,函数f(x)在区间(a,b)内有唯一的零点,即存在唯一的c∈(a,b),使f(c)=0.
②如果函数f(x)在区间[a,b]上的图象是连续不断的曲线,并且有f(a)·f(b)>0,那么,函数f(x)在区间(a,b)内不一定没有零点.2.函数综合题的求解往往应用多种知识和技能.因此,必须全面掌握有关的函数知识,并且严谨审题,弄清题目的已知条件,尤其要挖掘题目中的隐含条件.要认真分析,处理好各种关系,把握问题的主线,运用相关的知识和方法逐步化归为基本问题来解决.真题感悟押题精练真题与押题12真题感悟12真题感悟解析 作出函数f(x)的图象如图所示,其中A(1,1),B(0,-2).12真题感悟因为直线y=mx+m=m(x+1)恒过定点C(-1,0),故当直线y=m(x+1)在AC位置时,m= ,可知当直线y=m(x+1)在x轴和AC之间运动时两图象有两个不同的交点(直线y=m(x+1)可与AC重合但不能与x轴重合),此时0
率”.在特定条件下,可食用率p与加工时
间t(单位:分钟)满足函数关系p=at2+bt+
c(a、b、c是常数),如图记录了三次实验的
数据.根据上述函数模型和实验数据,可以
得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟真题感悟21解析 根据图表,把(t,p)的三组数据(3,0.7),(4,0.8),(5,0.5)分别代入函数关系式,真题感悟21即最佳加工时间为3.75分钟.
答案 B押题精练123解析 当f(x)=0时,x=-1或x=1,
故f[f(x)+1]=0时,f(x)+1=-1或1.当f(x)+1=-1,即f(x)=-2时,解得x=-3或x= ;押题精练123当f(x)+1=1,即f(x)=0时,解得x=-1或x=1.
故函数y=f[f(x)+1]有四个不同的零点.
答案 4押题精练1232.函数f(x)=xex-a有两个零点,则实数a的取值范围是________.解析 令f′(x)=(x+1)ex=0,得x=-1,
则当x∈(-∞,-1)时,f′(x)<0,
当x∈(-1,+∞)时,f′(x)>0,
f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,押题精练123要使f(x)有两个零点,则极小值f(-1)<0,即-e-1-a<0,∴a>- ,又x→-∞时,f(x)>0,则a<0,∴a∈(- ,0).答案 (- ,0)押题精练1233.某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*).则当每台机器运转________年时,年平均利润最大,最大值是________万元.押题精练123解析 由题意知每台机器运转x年的年平均利润为
=18-(x+ ),而x>0,故 ≤18-2 =8,当且仅当x=5时,年平均利润最大,最大值为8万元.
答案 5 8
同课章节目录
