【高考专辑】【专题23】2015年高三数学(理)【押题精练】空间中的平行与垂直
文档属性
| 名称 | 【高考专辑】【专题23】2015年高三数学(理)【押题精练】空间中的平行与垂直 |  | |
| 格式 | zip | ||
| 文件大小 | 621.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 18:58:00 | ||
图片预览







文档简介
课件57张PPT。专题23
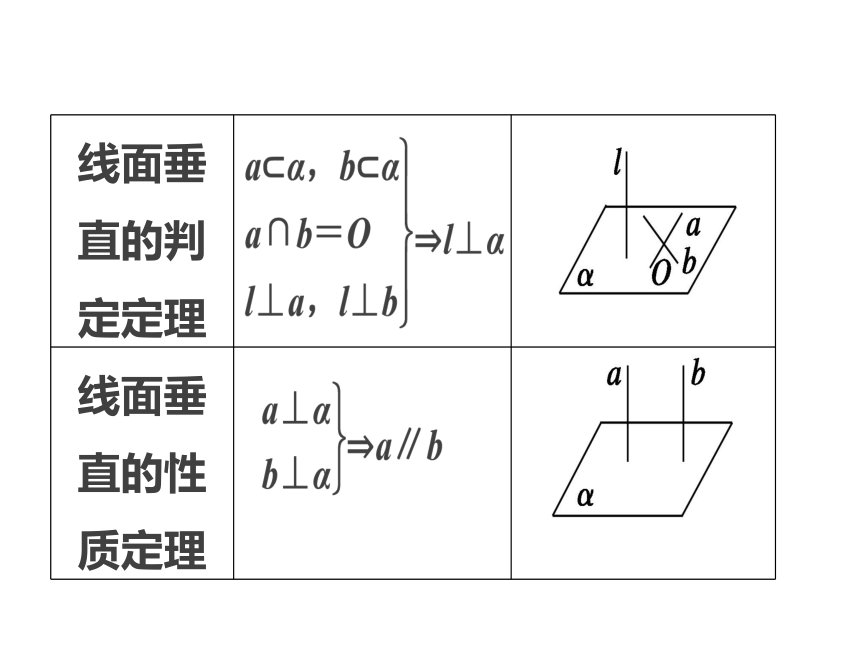
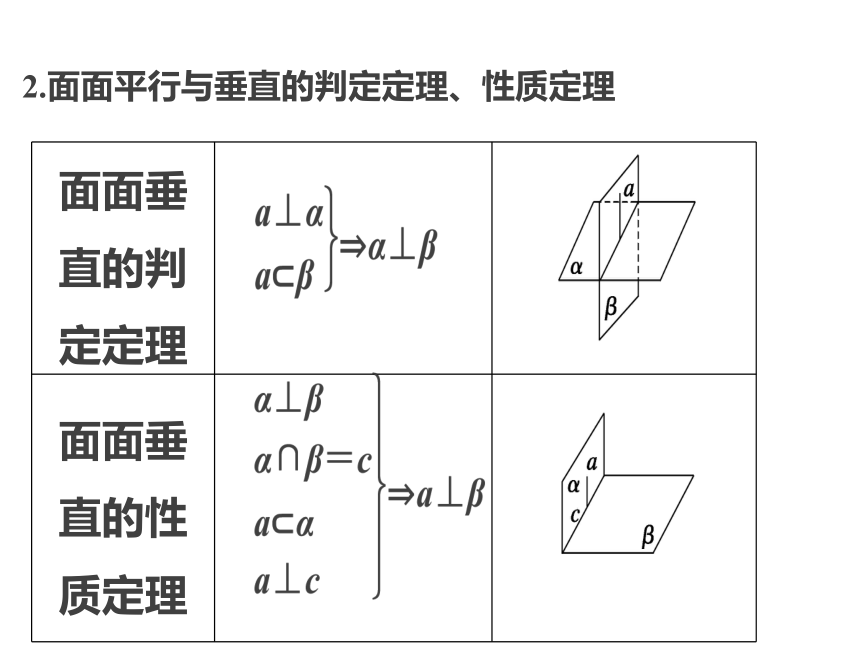
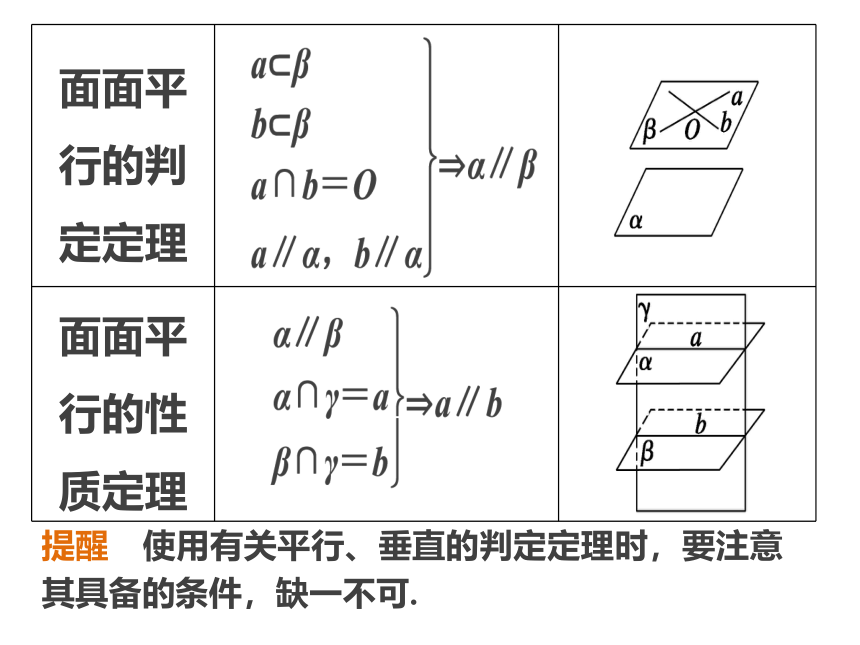
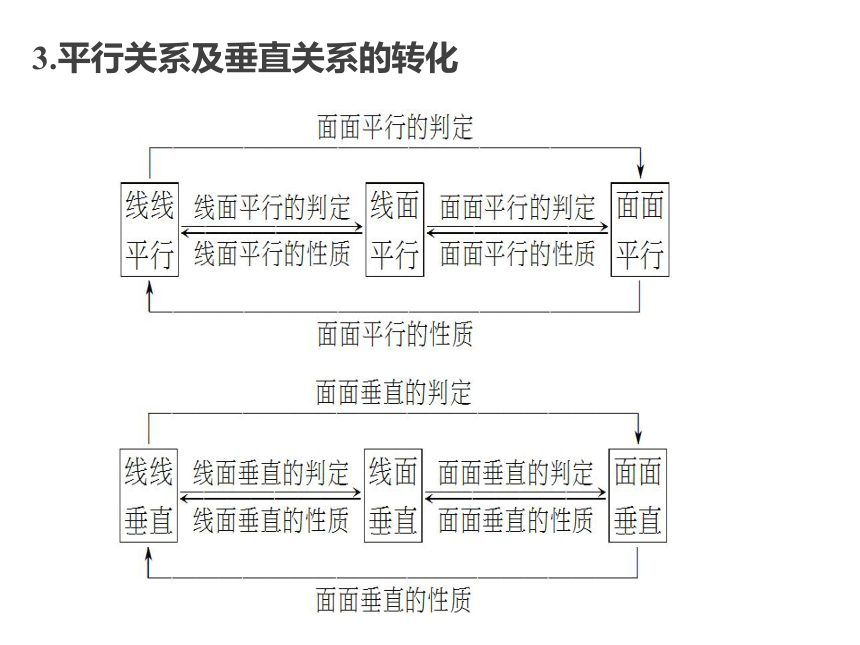
空间中的平行与垂直空间中的平行与垂直主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.线面平行与垂直的判定定理、性质定理2.面面平行与垂直的判定定理、性质定理提醒 使用有关平行、垂直的判定定理时,要注意其具备的条件,缺一不可.3.平行关系及垂直关系的转化热点一 空间线面位置关系的判定热点二 平行、垂直关系的证明热点三 图形的折叠问题热点分类突破例1 (1)设a,b表示直线,α,β,γ表示不同的平面,则下列命题中正确的是( )
A.若a⊥α且a⊥b,则b∥α
B.若γ⊥α且γ⊥β,则α∥β
C.若a∥α且a∥β,则α∥β
D.若γ∥α且γ∥β,则α∥β热点一 空间线面位置关系的判定思维启迪
判断空间线面关系的基本思路:利用定理或结论;借助实物模型作出肯定或否定.解析 A:应该是b∥α或b?α;
B:如果是墙角出发的三个面就不符合题意;
C:α∩β=m,若a∥m时,满足a∥α,a∥β,但是α∥β不正确,所以选D.
答案 D(2)平面α∥平面β的一个充分条件是( )
A.存在一条直线a,a∥α,a∥β
B.存在一条直线a,a?α,a∥β
C.存在两条平行直线a,b,a?α,b?β,a∥β,b∥α
D.存在两条异面直线a,b,a?α,b?β,a∥β,b∥α解析 若α∩β=l,a∥l,a?α,a?β,则a∥α,a∥β,故排除A.
若α∩β=l,a?α,a∥l,则a∥β,故排除B.
若α∩β=l,a?α,a∥l,b?β,b∥l,则a∥β,b∥α,故排除C.故选D.
答案 D变式训练1设m、n是不同的直线,α、β是不同的平面,有以下四个命题:
①若α⊥β,m∥α,则m⊥β ②若m⊥α,n⊥α,则m∥n
③若m⊥α,m⊥n,则n∥α ④若n⊥α,n⊥β,则β∥α
其中真命题的序号为( )
A.①③ B.②③ C.①④ D.②④解析 ①若α⊥β,m∥α,则m与β可以是直线与平面的所有关系,所以①错误;
②若m⊥α,n⊥α,则m∥n,所以②正确;
③若m⊥α,m⊥n,则n∥α或n?α,所以③错误;
④若n⊥α,n⊥β,则β∥α,所以④正确.
故选D.
答案 D例2 如图,在四棱锥P-ABCD中,
AB∥CD,AB⊥AD,CD=2AB,平
面PAD⊥底面ABCD,PA⊥AD,E和
F分别是CD和PC的中点,求证:
(1)PA⊥底面ABCD;热点二 平行、垂直关系的证明(1)PA⊥底面ABCD;思维启迪
利用平面PAD⊥底面ABCD的性质,得线面垂直;证明 因为平面PAD⊥底面ABCD,
且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.(2)BE∥平面PAD;思维启迪 BE∥AD易证;证明 因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.
所以BE∥AD.
又因为BE?平面PAD,AD?平面PAD,
所以BE∥平面PAD.(3)平面BEF⊥平面PCD.思维启迪 EF是△CPD的中位线.证明 因为AB⊥AD,而且ABED为平行四边形.
所以BE⊥CD,AD⊥CD,
由(1)知PA⊥底面ABCD.
所以PA⊥CD.
所以CD⊥平面PAD.
所以CD⊥PD.因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
又CD?平面PCD,
所以平面BEF⊥平面PCD.变式训练2 如图所示,已知AB⊥平面ACD,DE⊥
平面ACD,△ACD为等边三角形,AD
=DE=2AB,F为CD的中点.
求证:(1)AF∥平面BCE;证明 如图,取CE的中点G,连接FG,BG.∵F为CD的中点,∴GF∥DE且GF= DE.∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.又AB= DE,∴GF=AB.∴四边形GFAB为平行四边形,则AF∥BG.
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE.(2)平面BCE⊥平面CDE.证明 ∵△ACD为等边三角形,F为CD的中点,
∴AF⊥CD.
∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF.
又CD∩DE=D,∴AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.例3 如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).热点三 图形的折叠问题(1)求证:DE∥平面A1CB;思维启迪
折叠问题要注意在折叠过程中,哪些量变化了,哪些量没有变化.第(1)问证明线面平行,可以证明DE∥BC;证明 因为D,E分别为AC,AB的中点,
所以DE∥BC.
又因为DE?平面A1CB,BC?平面A1CB,
所以DE∥平面A1CB.(2)求证:A1F⊥BE;思维启迪
第(2)问证明线线垂直转化为证明线面垂直,即证明A1F⊥平面BCDE;证明 由题图(1)得AC⊥BC且DE∥BC,
所以DE⊥AC.所以DE⊥A1D,DE⊥CD.
所以DE⊥平面A1DC.而A1F?平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,
所以A1F⊥平面BCDE,又BE?平面BCDE,
所以A1F⊥BE.(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?请说明理由.思维启迪
第(3)问取A1B的中点Q,再证明A1C⊥平面DEQ.解 线段A1B上存在点Q,使A1C⊥平面
DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,
则PQ∥BC.又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.变式训练3如图(1),已知梯形ABCD中,AD∥BC,∠BAD= ,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图(2)所示),G是BC的中点.(1)当x=2时,求证:BD⊥EG;证明 作DH⊥EF,垂足为H,
连接BH,GH,因为平面AEFD⊥平面EBCF,交
线为EF,DH?平面AEFD,
所以DH⊥平面EBCF,又EG?平面EBCF,
故EG⊥DH.因为EH=AD= BC=BG=2,BE=2,EF∥BC,∠EBC=90°,所以四边形BGHE为正方形,故EG⊥BH.
又BH,DH?平面DBH,且BH∩DH=H,
故EG⊥平面DBH.
又BD?平面DBH,故EG⊥BD.(2)当x变化时,求三棱锥D-BCF的体积f(x)的函数式.解 因为AE⊥EF,平面AEFD⊥平面EBCF,交线为EF,AE?平面AEFD,
所以AE⊥平面EBCF.
由(1)知,DH⊥平面EBCF,故AE∥DH,
所以四边形AEHD是矩形,DH=AE,
故以B,F,C,D为顶点的三棱锥D-BCF的高
DH=AE=x.1.证明线线平行的常用方法
(1)利用平行公理,即证明两直线同时和第三条直线平行;
(2)利用平行四边形进行转换;
(3)利用三角形中位线定理证明;
(4)利用线面平行、面面平行的性质定理证明.本讲规律总结2.证明线面平行的常用方法
(1)利用线面平行的判定定理,把证明线面平行转化为证线线平行;
(2)利用面面平行的性质定理,把证明线面平行转化为证面面平行.
3.证明面面平行的方法
证明面面平行,依据判定定理,只要找到一个面内两条相交直线与另一个平面平行即可,从而将证面面平行转化为证线面平行,再转化为证线线平行.4.证明线线垂直的常用方法
(1)利用特殊平面图形的性质,如利用直角三角形、矩形、菱形、等腰三角形等得到线线垂直;
(2)利用勾股定理逆定理;
(3)利用线面垂直的性质,即要证线线垂直,只需证明一线垂直于另一线所在平面即可.5.证明线面垂直的常用方法
(1)利用线面垂直的判定定理,把线面垂直的判定转化为证明线线垂直;
(2)利用面面垂直的性质定理,把证明线面垂直转化为证面面垂直;
(3)利用常见结论,如两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.6.证明面面垂直的方法
证明面面垂直常用面面垂直的判定定理,即证明一个面过另一个面的一条垂线,将证明面面垂直转化为证明线面垂直,一般先从现有直线中寻找,若图中不存在这样的直线,则借助中点、高线或添加辅助线解决.真题感悟押题精练真题与押题12真题感悟1.(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥α12真题感悟解析 方法一 若m∥α,n∥α,
则m,n可能平行、相交或异面,A错;
若m⊥α,n?α,则m⊥n,因为直线与平面垂直时,它垂直于平面内任一直线,B正确;
若m⊥α,m⊥n,则n∥α或n?α,C错;
若m∥α,m⊥n,则n与α可能相交,可能平行,也可能n?α,D错.12真题感悟方法二 如图,在正方体ABCD-
A′B′C′D′中,用平面ABCD表示α.
A项中,若m为A′B′,n为B′C′,
满足m∥α,n∥α,
但m与n是相交直线,故A错.
B项中,m⊥α,n?α,
∴m⊥n,这是线面垂直的性质,故B正确.12真题感悟C项中,若m为AA′,n为AB,
满足m⊥α,m⊥n,但n?α,故C错.
D项中,若m为A′B′,n为B′C′,
满足m∥α,m⊥n,但n∥α,故D错.
答案 B真题感悟212.(2014·辽宁)如图,△ABC和△BCD
所在平面互相垂直,且AB=BC=BD
=2,∠ABC=∠DBC=120°,E,
F,G分别为AC,DC,AD的中点.真题感悟21(1)求证:EF⊥平面BCG;证明 由已知得△ABC≌△DBC,因此AC=DC.
又G为AD的中点,所以CG⊥AD.
同理BG⊥AD,又BG∩CG=G,
因此AD⊥平面BGC.
又EF∥AD,所以EF⊥平面BCG.真题感悟21(2)求三棱锥D-BCG的体积.
附:锥体的体积公式V= Sh,其中S为底面面积,h为高.解 在平面ABC内,作AO⊥BC,交CB的延长线于O.
由平面ABC⊥平面BCD,知AO⊥平面BDC.
又G为AD中点,因此G到平面BDC的距离h是AO长度的一半.真题感悟21押题精练121. 如图,AB为圆O的直径,点C在圆周上(异
于点A,B),直线PA垂直于圆O所在的平面,
点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;
②MO∥平面PAC;
③OC⊥平面PAC;
④平面PAC⊥平面PBC.
其中正确的命题是________(填上所有正确命题的序号).押题精练12解析 ①错误,PA?平面MOB;
②正确;
③错误,否则,有OC⊥AC,这与BC⊥AC矛盾;
④正确,因为BC⊥平面PAC.
答案 ②④押题精练122.如图所示,在正方体ABCD-A1B1C1D1
中,E是棱DD1的中点.
(1)证明:平面ADC1B1⊥平面A1BE;证明 如图,因为ABCD-A1B1C1D1为正方体,
所以B1C1⊥面ABB1A1.
因为A1B?面ABB1A1,所以B1C1⊥A1B.押题精练12又因为A1B⊥AB1,B1C1∩AB1=B1,
所以A1B⊥面ADC1B1.
因为A1B?面A1BE,
所以平面ADC1B1⊥平面A1BE.押题精练12(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?并证明你的结论.解 当点F为C1D1中点时,可使B1F∥平面A1BE.
证明如下:取C1D1中点F,连接EF,B1F易知:EF∥C1D,且EF= C1D.押题精练12设AB1∩A1B=O,连接OE,则B1O∥C1D且B1O= C1D,所以EF∥B1O且EF=B1O,
所以四边形B1OEF为平行四边形.
所以B1F∥OE.
又因为B1F?面A1BE,OE?面A1BE.
所以B1F∥面A1BE.
空间中的平行与垂直空间中的平行与垂直主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.线面平行与垂直的判定定理、性质定理2.面面平行与垂直的判定定理、性质定理提醒 使用有关平行、垂直的判定定理时,要注意其具备的条件,缺一不可.3.平行关系及垂直关系的转化热点一 空间线面位置关系的判定热点二 平行、垂直关系的证明热点三 图形的折叠问题热点分类突破例1 (1)设a,b表示直线,α,β,γ表示不同的平面,则下列命题中正确的是( )
A.若a⊥α且a⊥b,则b∥α
B.若γ⊥α且γ⊥β,则α∥β
C.若a∥α且a∥β,则α∥β
D.若γ∥α且γ∥β,则α∥β热点一 空间线面位置关系的判定思维启迪
判断空间线面关系的基本思路:利用定理或结论;借助实物模型作出肯定或否定.解析 A:应该是b∥α或b?α;
B:如果是墙角出发的三个面就不符合题意;
C:α∩β=m,若a∥m时,满足a∥α,a∥β,但是α∥β不正确,所以选D.
答案 D(2)平面α∥平面β的一个充分条件是( )
A.存在一条直线a,a∥α,a∥β
B.存在一条直线a,a?α,a∥β
C.存在两条平行直线a,b,a?α,b?β,a∥β,b∥α
D.存在两条异面直线a,b,a?α,b?β,a∥β,b∥α解析 若α∩β=l,a∥l,a?α,a?β,则a∥α,a∥β,故排除A.
若α∩β=l,a?α,a∥l,则a∥β,故排除B.
若α∩β=l,a?α,a∥l,b?β,b∥l,则a∥β,b∥α,故排除C.故选D.
答案 D变式训练1设m、n是不同的直线,α、β是不同的平面,有以下四个命题:
①若α⊥β,m∥α,则m⊥β ②若m⊥α,n⊥α,则m∥n
③若m⊥α,m⊥n,则n∥α ④若n⊥α,n⊥β,则β∥α
其中真命题的序号为( )
A.①③ B.②③ C.①④ D.②④解析 ①若α⊥β,m∥α,则m与β可以是直线与平面的所有关系,所以①错误;
②若m⊥α,n⊥α,则m∥n,所以②正确;
③若m⊥α,m⊥n,则n∥α或n?α,所以③错误;
④若n⊥α,n⊥β,则β∥α,所以④正确.
故选D.
答案 D例2 如图,在四棱锥P-ABCD中,
AB∥CD,AB⊥AD,CD=2AB,平
面PAD⊥底面ABCD,PA⊥AD,E和
F分别是CD和PC的中点,求证:
(1)PA⊥底面ABCD;热点二 平行、垂直关系的证明(1)PA⊥底面ABCD;思维启迪
利用平面PAD⊥底面ABCD的性质,得线面垂直;证明 因为平面PAD⊥底面ABCD,
且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.(2)BE∥平面PAD;思维启迪 BE∥AD易证;证明 因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.
所以BE∥AD.
又因为BE?平面PAD,AD?平面PAD,
所以BE∥平面PAD.(3)平面BEF⊥平面PCD.思维启迪 EF是△CPD的中位线.证明 因为AB⊥AD,而且ABED为平行四边形.
所以BE⊥CD,AD⊥CD,
由(1)知PA⊥底面ABCD.
所以PA⊥CD.
所以CD⊥平面PAD.
所以CD⊥PD.因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
又CD?平面PCD,
所以平面BEF⊥平面PCD.变式训练2 如图所示,已知AB⊥平面ACD,DE⊥
平面ACD,△ACD为等边三角形,AD
=DE=2AB,F为CD的中点.
求证:(1)AF∥平面BCE;证明 如图,取CE的中点G,连接FG,BG.∵F为CD的中点,∴GF∥DE且GF= DE.∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.又AB= DE,∴GF=AB.∴四边形GFAB为平行四边形,则AF∥BG.
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE.(2)平面BCE⊥平面CDE.证明 ∵△ACD为等边三角形,F为CD的中点,
∴AF⊥CD.
∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF.
又CD∩DE=D,∴AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.例3 如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).热点三 图形的折叠问题(1)求证:DE∥平面A1CB;思维启迪
折叠问题要注意在折叠过程中,哪些量变化了,哪些量没有变化.第(1)问证明线面平行,可以证明DE∥BC;证明 因为D,E分别为AC,AB的中点,
所以DE∥BC.
又因为DE?平面A1CB,BC?平面A1CB,
所以DE∥平面A1CB.(2)求证:A1F⊥BE;思维启迪
第(2)问证明线线垂直转化为证明线面垂直,即证明A1F⊥平面BCDE;证明 由题图(1)得AC⊥BC且DE∥BC,
所以DE⊥AC.所以DE⊥A1D,DE⊥CD.
所以DE⊥平面A1DC.而A1F?平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,
所以A1F⊥平面BCDE,又BE?平面BCDE,
所以A1F⊥BE.(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?请说明理由.思维启迪
第(3)问取A1B的中点Q,再证明A1C⊥平面DEQ.解 线段A1B上存在点Q,使A1C⊥平面
DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,
则PQ∥BC.又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.变式训练3如图(1),已知梯形ABCD中,AD∥BC,∠BAD= ,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图(2)所示),G是BC的中点.(1)当x=2时,求证:BD⊥EG;证明 作DH⊥EF,垂足为H,
连接BH,GH,因为平面AEFD⊥平面EBCF,交
线为EF,DH?平面AEFD,
所以DH⊥平面EBCF,又EG?平面EBCF,
故EG⊥DH.因为EH=AD= BC=BG=2,BE=2,EF∥BC,∠EBC=90°,所以四边形BGHE为正方形,故EG⊥BH.
又BH,DH?平面DBH,且BH∩DH=H,
故EG⊥平面DBH.
又BD?平面DBH,故EG⊥BD.(2)当x变化时,求三棱锥D-BCF的体积f(x)的函数式.解 因为AE⊥EF,平面AEFD⊥平面EBCF,交线为EF,AE?平面AEFD,
所以AE⊥平面EBCF.
由(1)知,DH⊥平面EBCF,故AE∥DH,
所以四边形AEHD是矩形,DH=AE,
故以B,F,C,D为顶点的三棱锥D-BCF的高
DH=AE=x.1.证明线线平行的常用方法
(1)利用平行公理,即证明两直线同时和第三条直线平行;
(2)利用平行四边形进行转换;
(3)利用三角形中位线定理证明;
(4)利用线面平行、面面平行的性质定理证明.本讲规律总结2.证明线面平行的常用方法
(1)利用线面平行的判定定理,把证明线面平行转化为证线线平行;
(2)利用面面平行的性质定理,把证明线面平行转化为证面面平行.
3.证明面面平行的方法
证明面面平行,依据判定定理,只要找到一个面内两条相交直线与另一个平面平行即可,从而将证面面平行转化为证线面平行,再转化为证线线平行.4.证明线线垂直的常用方法
(1)利用特殊平面图形的性质,如利用直角三角形、矩形、菱形、等腰三角形等得到线线垂直;
(2)利用勾股定理逆定理;
(3)利用线面垂直的性质,即要证线线垂直,只需证明一线垂直于另一线所在平面即可.5.证明线面垂直的常用方法
(1)利用线面垂直的判定定理,把线面垂直的判定转化为证明线线垂直;
(2)利用面面垂直的性质定理,把证明线面垂直转化为证面面垂直;
(3)利用常见结论,如两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.6.证明面面垂直的方法
证明面面垂直常用面面垂直的判定定理,即证明一个面过另一个面的一条垂线,将证明面面垂直转化为证明线面垂直,一般先从现有直线中寻找,若图中不存在这样的直线,则借助中点、高线或添加辅助线解决.真题感悟押题精练真题与押题12真题感悟1.(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥α12真题感悟解析 方法一 若m∥α,n∥α,
则m,n可能平行、相交或异面,A错;
若m⊥α,n?α,则m⊥n,因为直线与平面垂直时,它垂直于平面内任一直线,B正确;
若m⊥α,m⊥n,则n∥α或n?α,C错;
若m∥α,m⊥n,则n与α可能相交,可能平行,也可能n?α,D错.12真题感悟方法二 如图,在正方体ABCD-
A′B′C′D′中,用平面ABCD表示α.
A项中,若m为A′B′,n为B′C′,
满足m∥α,n∥α,
但m与n是相交直线,故A错.
B项中,m⊥α,n?α,
∴m⊥n,这是线面垂直的性质,故B正确.12真题感悟C项中,若m为AA′,n为AB,
满足m⊥α,m⊥n,但n?α,故C错.
D项中,若m为A′B′,n为B′C′,
满足m∥α,m⊥n,但n∥α,故D错.
答案 B真题感悟212.(2014·辽宁)如图,△ABC和△BCD
所在平面互相垂直,且AB=BC=BD
=2,∠ABC=∠DBC=120°,E,
F,G分别为AC,DC,AD的中点.真题感悟21(1)求证:EF⊥平面BCG;证明 由已知得△ABC≌△DBC,因此AC=DC.
又G为AD的中点,所以CG⊥AD.
同理BG⊥AD,又BG∩CG=G,
因此AD⊥平面BGC.
又EF∥AD,所以EF⊥平面BCG.真题感悟21(2)求三棱锥D-BCG的体积.
附:锥体的体积公式V= Sh,其中S为底面面积,h为高.解 在平面ABC内,作AO⊥BC,交CB的延长线于O.
由平面ABC⊥平面BCD,知AO⊥平面BDC.
又G为AD中点,因此G到平面BDC的距离h是AO长度的一半.真题感悟21押题精练121. 如图,AB为圆O的直径,点C在圆周上(异
于点A,B),直线PA垂直于圆O所在的平面,
点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;
②MO∥平面PAC;
③OC⊥平面PAC;
④平面PAC⊥平面PBC.
其中正确的命题是________(填上所有正确命题的序号).押题精练12解析 ①错误,PA?平面MOB;
②正确;
③错误,否则,有OC⊥AC,这与BC⊥AC矛盾;
④正确,因为BC⊥平面PAC.
答案 ②④押题精练122.如图所示,在正方体ABCD-A1B1C1D1
中,E是棱DD1的中点.
(1)证明:平面ADC1B1⊥平面A1BE;证明 如图,因为ABCD-A1B1C1D1为正方体,
所以B1C1⊥面ABB1A1.
因为A1B?面ABB1A1,所以B1C1⊥A1B.押题精练12又因为A1B⊥AB1,B1C1∩AB1=B1,
所以A1B⊥面ADC1B1.
因为A1B?面A1BE,
所以平面ADC1B1⊥平面A1BE.押题精练12(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?并证明你的结论.解 当点F为C1D1中点时,可使B1F∥平面A1BE.
证明如下:取C1D1中点F,连接EF,B1F易知:EF∥C1D,且EF= C1D.押题精练12设AB1∩A1B=O,连接OE,则B1O∥C1D且B1O= C1D,所以EF∥B1O且EF=B1O,
所以四边形B1OEF为平行四边形.
所以B1F∥OE.
又因为B1F?面A1BE,OE?面A1BE.
所以B1F∥面A1BE.
同课章节目录
