【高考专辑】【专题25】2015年高三数学(理)【押题精练】椭圆、双曲线、抛物线
文档属性
| 名称 | 【高考专辑】【专题25】2015年高三数学(理)【押题精练】椭圆、双曲线、抛物线 |  | |
| 格式 | zip | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 19:00:39 | ||
图片预览



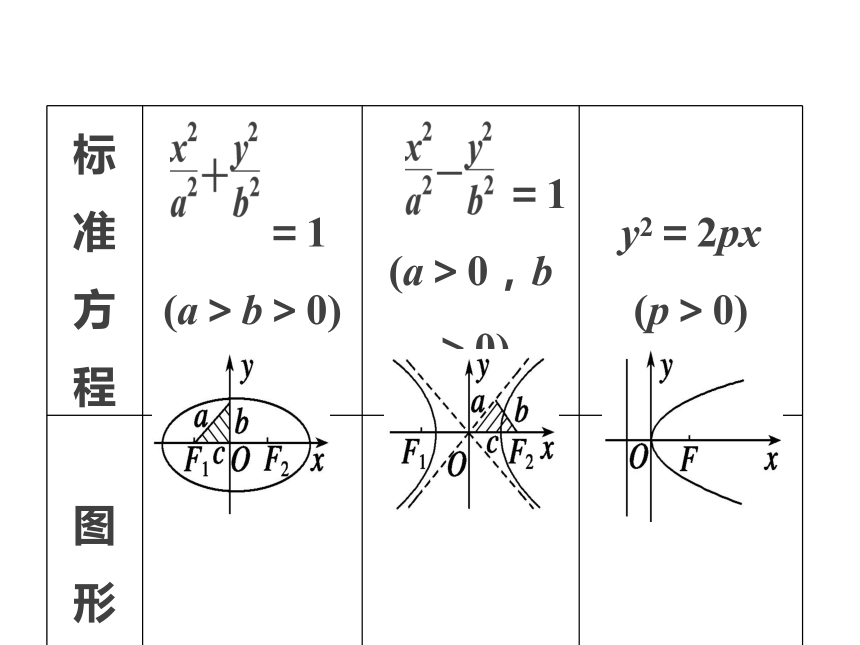





文档简介
课件66张PPT。专题25
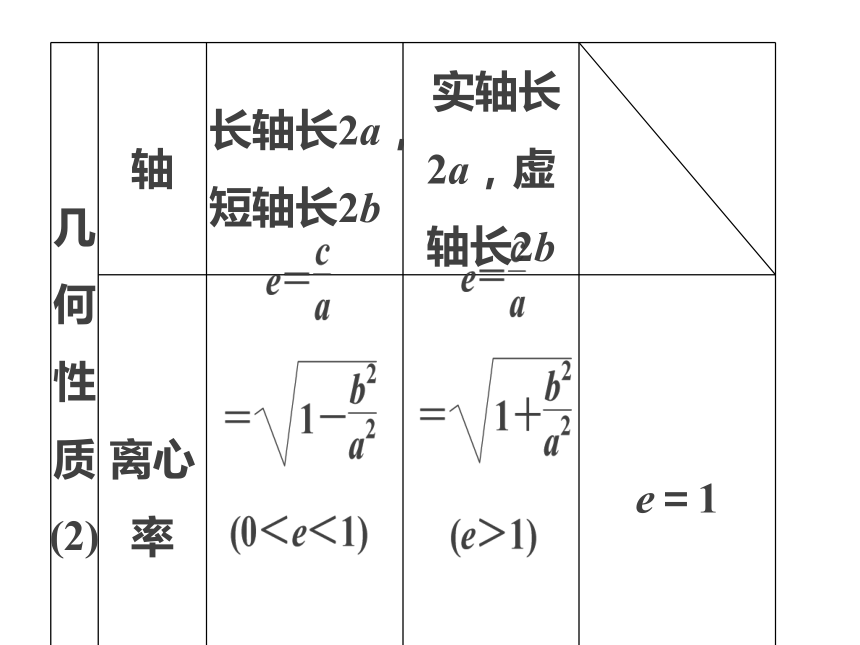
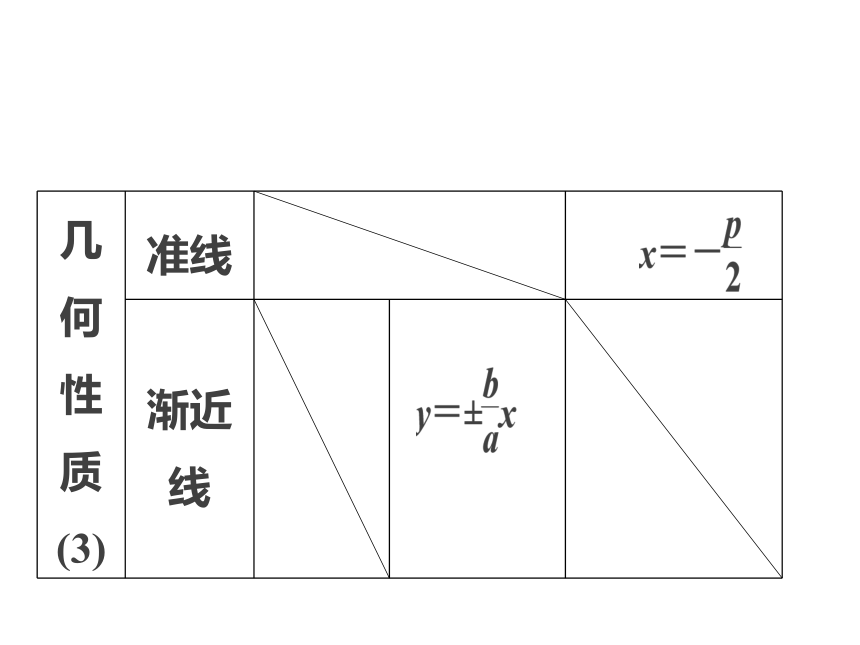
椭圆、双曲线、抛物线椭圆、双曲线、抛物线主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理圆锥曲线的定义、标准方程与几何性质热点一 圆锥曲线的定义与标准方程热点二 圆锥曲线的几何性质热点三 直线与圆锥曲线热点分类突破热点一 圆锥曲线的定义与标准方程思维启迪
△PF1F2中利用余弦定理求∠F1PF2;解析 由题意得a=3,c= ,所以|PF1|=2.在△F2PF1中,又因为cos∠F2PF1∈(0°,180°),
所以∠F2PF1=120°.
答案 C(2)已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-
的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为________.思维启迪
根据抛物线定义得m=|PF|-1.再利用数形结合求最值.解析 易知x2=2py(p>0)的焦点为F(0,1),故p=2,
因此抛物线方程为x2=4y.
根据抛物线的定义可知m=|PF|-1,
设|PH|=n(H为点P到直线l所作垂线的垂足),
因此m+n=|PF|-1+|PH|.
易知当F,P,H三点共线时m+n最小,变式训练1∴a=2b.∴椭圆方程为x2+4y2=4b2.
∵双曲线x2-y2=1的渐近线方程为x±y=0,答案 D(2)如图,过抛物线y2=2px(p>0)的焦点F
的直线交抛物线于点A,B,交其准线l于
点C,若|BC|=2|BF|,且|AF|=3,则此抛
物线的方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2= x解析 如图,分别过A,B作AA1⊥l于A1,
BB1⊥l于B1,由抛物线的定义知,
|AF|=|AA1|,|BF|=|BB1|,
∵|BC|=2|BF|,∴|BC|=2|BB1|,
∴∠BCB1=30°,∴∠A1AF=60°.
连接A1F,则△A1AF为等边三角形,过F作FF1⊥AA1于F1,则F1为AA1的中点,∴抛物线方程为y2=3x,故选C.
答案 C热点二 圆锥曲线的几何性质思维启迪
在△F1F2P中利用余弦定理列方程,然后利用定义和已知条件消元;解析 设椭圆的长半轴长为a1,双曲线的实半轴长为a2,焦距为2c,|PF1|=m,|PF2|=n,且不妨设m>n,
由m+n=2a1,m-n=2a2得m=a1+a2,n=a1-a2.答案 C思维启迪
可设点P坐标为( ,y),考察y存在的条件.但注意到b2-2c2≠0,即2c2-b2>0,当 不存在时,b2-2c2=0,y=0,答案 D变式训练2 ∴AC⊥OF,∴AO=AF,又∠OAF=90°,∴∠AOF=45°,即双曲线的渐近线的倾斜角为45°,答案 C答案 A热点三 直线与圆锥曲线(1)求椭圆的离心率;思维启迪
根据 和点B在椭圆上列关于a、b的方程;解 ∵A(-a,0),设直线方程为y=2(x+a),B(x1,y1),
令x=0,则y=2a,∴C(0,2a),(2)设动直线y=kx+m与椭圆有且只有一个公共点P,且与直线x=4相交于点Q,若x轴上存在一定点M(1,0),使得PM⊥QM,求椭圆的方程.思维启迪
联立直线y=kx+m与椭圆方程,利用Δ=0,
=0求解.∴椭圆的方程为3x2+4y2-12t=0,得(3+4k2)x2+8kmx+4m2-12t=0,∵动直线y=kx+m与椭圆有且只有一个公共点P,∴Δ=0,即64k2m2-4(3+4k2)(4m2-12t)=0,
整理得m2=3t+4k2t,又M(1,0),Q(4,4k+m),
∵x轴上存在一定点M(1,0),使得PM⊥QM,整理得3+4k2=m2.
∴3+4k2=3t+4k2t恒成立,故t=1.变式训练3(1)求椭圆C的方程;解 因为焦距为2,所以a2-b2=1.当直线AB不垂直于x轴时,则-1+4mk=0,故4mk=1.此时,直线PQ的斜率为k1=-4m,即y=-4mx-m.整理得(32m2+1)x2+16m2x+2m2-2=0.
设P(x3,y3),Q(x4,y4)=(4m2-1)(x3+x4)+(16m2+1)x3x4+m2+11.对涉及圆锥曲线上点到焦点距离或焦点弦的问题,恰当选用定义解题,会效果明显,定义中的定值是标准方程的基础.
2.椭圆、双曲线的方程形式上可统一为Ax2+By2=1,其中A、B是不等的常数,A>B>0时,表示焦点在y轴上的椭圆;B>A>0时,表示焦点在x轴上的椭圆;AB<0时表示双曲线.本讲规律总结真题感悟押题精练真题与押题12真题感悟12真题感悟解析 设|PF1|=r1,|PF2|=r2(r1>r2),|F1F2|=2c,
椭圆长半轴长为a1,双曲线实半轴长为a2,椭圆、双曲线的离心率分别为e1,e2,12真题感悟答案 A真题感悟212.(2014·辽宁)已知点A(-2,3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )解析 抛物线y2=2px的准线为直线x=- ,而点A(-2,3)在准线上,真题感悟21所以- =-2,即p=4,从而C:y2=8x,焦点为F(2,0).设切线方程为y-3=k(x+2),代入y2=8x得 y2-y+2k+3=0(k≠0)①,真题感悟21由于Δ=1-4× (2k+3)=0,所以k=-2或k= .因为切点在第一象限,所以k= .将k= 代入①中,得y=8,再代入y2=8x中得x=8,所以点B的坐标为(8,8),所以直线BF的斜率为 .答案 D押题精练12押题精练12解析 如图所示,
设双曲线的右焦点为H,连接PH,由双曲线的性质,可知O为FH的中点,押题精练12由双曲线的定义,可知|PF|-|PH|=2a(P在双曲线的右支上),因为直线l与圆相切,所以PF⊥OE.又OE∥PH,所以PF⊥PH.押题精练12在△PFH中,|FH|2=|PH|2+|PF|2,押题精练12押题精练12解 设点P的坐标为(x0,y0),y0≠0.押题精练12证明 方法一 依题意,直线OP的方程为y=kx,由|AP|=|OA|,A(-a,0)及y0=kx0,押题精练12又a>b>0,故(1+k2)2>4k2+4,即k2+1>4,押题精练12方法二 依题意,直线OP的方程为y=kx,
可设点P的坐标为(x0,kx0).因为a>b>0,kx0≠0,押题精练12
椭圆、双曲线、抛物线椭圆、双曲线、抛物线主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理圆锥曲线的定义、标准方程与几何性质热点一 圆锥曲线的定义与标准方程热点二 圆锥曲线的几何性质热点三 直线与圆锥曲线热点分类突破热点一 圆锥曲线的定义与标准方程思维启迪
△PF1F2中利用余弦定理求∠F1PF2;解析 由题意得a=3,c= ,所以|PF1|=2.在△F2PF1中,又因为cos∠F2PF1∈(0°,180°),
所以∠F2PF1=120°.
答案 C(2)已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-
的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为________.思维启迪
根据抛物线定义得m=|PF|-1.再利用数形结合求最值.解析 易知x2=2py(p>0)的焦点为F(0,1),故p=2,
因此抛物线方程为x2=4y.
根据抛物线的定义可知m=|PF|-1,
设|PH|=n(H为点P到直线l所作垂线的垂足),
因此m+n=|PF|-1+|PH|.
易知当F,P,H三点共线时m+n最小,变式训练1∴a=2b.∴椭圆方程为x2+4y2=4b2.
∵双曲线x2-y2=1的渐近线方程为x±y=0,答案 D(2)如图,过抛物线y2=2px(p>0)的焦点F
的直线交抛物线于点A,B,交其准线l于
点C,若|BC|=2|BF|,且|AF|=3,则此抛
物线的方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2= x解析 如图,分别过A,B作AA1⊥l于A1,
BB1⊥l于B1,由抛物线的定义知,
|AF|=|AA1|,|BF|=|BB1|,
∵|BC|=2|BF|,∴|BC|=2|BB1|,
∴∠BCB1=30°,∴∠A1AF=60°.
连接A1F,则△A1AF为等边三角形,过F作FF1⊥AA1于F1,则F1为AA1的中点,∴抛物线方程为y2=3x,故选C.
答案 C热点二 圆锥曲线的几何性质思维启迪
在△F1F2P中利用余弦定理列方程,然后利用定义和已知条件消元;解析 设椭圆的长半轴长为a1,双曲线的实半轴长为a2,焦距为2c,|PF1|=m,|PF2|=n,且不妨设m>n,
由m+n=2a1,m-n=2a2得m=a1+a2,n=a1-a2.答案 C思维启迪
可设点P坐标为( ,y),考察y存在的条件.但注意到b2-2c2≠0,即2c2-b2>0,当 不存在时,b2-2c2=0,y=0,答案 D变式训练2 ∴AC⊥OF,∴AO=AF,又∠OAF=90°,∴∠AOF=45°,即双曲线的渐近线的倾斜角为45°,答案 C答案 A热点三 直线与圆锥曲线(1)求椭圆的离心率;思维启迪
根据 和点B在椭圆上列关于a、b的方程;解 ∵A(-a,0),设直线方程为y=2(x+a),B(x1,y1),
令x=0,则y=2a,∴C(0,2a),(2)设动直线y=kx+m与椭圆有且只有一个公共点P,且与直线x=4相交于点Q,若x轴上存在一定点M(1,0),使得PM⊥QM,求椭圆的方程.思维启迪
联立直线y=kx+m与椭圆方程,利用Δ=0,
=0求解.∴椭圆的方程为3x2+4y2-12t=0,得(3+4k2)x2+8kmx+4m2-12t=0,∵动直线y=kx+m与椭圆有且只有一个公共点P,∴Δ=0,即64k2m2-4(3+4k2)(4m2-12t)=0,
整理得m2=3t+4k2t,又M(1,0),Q(4,4k+m),
∵x轴上存在一定点M(1,0),使得PM⊥QM,整理得3+4k2=m2.
∴3+4k2=3t+4k2t恒成立,故t=1.变式训练3(1)求椭圆C的方程;解 因为焦距为2,所以a2-b2=1.当直线AB不垂直于x轴时,则-1+4mk=0,故4mk=1.此时,直线PQ的斜率为k1=-4m,即y=-4mx-m.整理得(32m2+1)x2+16m2x+2m2-2=0.
设P(x3,y3),Q(x4,y4)=(4m2-1)(x3+x4)+(16m2+1)x3x4+m2+11.对涉及圆锥曲线上点到焦点距离或焦点弦的问题,恰当选用定义解题,会效果明显,定义中的定值是标准方程的基础.
2.椭圆、双曲线的方程形式上可统一为Ax2+By2=1,其中A、B是不等的常数,A>B>0时,表示焦点在y轴上的椭圆;B>A>0时,表示焦点在x轴上的椭圆;AB<0时表示双曲线.本讲规律总结真题感悟押题精练真题与押题12真题感悟12真题感悟解析 设|PF1|=r1,|PF2|=r2(r1>r2),|F1F2|=2c,
椭圆长半轴长为a1,双曲线实半轴长为a2,椭圆、双曲线的离心率分别为e1,e2,12真题感悟答案 A真题感悟212.(2014·辽宁)已知点A(-2,3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )解析 抛物线y2=2px的准线为直线x=- ,而点A(-2,3)在准线上,真题感悟21所以- =-2,即p=4,从而C:y2=8x,焦点为F(2,0).设切线方程为y-3=k(x+2),代入y2=8x得 y2-y+2k+3=0(k≠0)①,真题感悟21由于Δ=1-4× (2k+3)=0,所以k=-2或k= .因为切点在第一象限,所以k= .将k= 代入①中,得y=8,再代入y2=8x中得x=8,所以点B的坐标为(8,8),所以直线BF的斜率为 .答案 D押题精练12押题精练12解析 如图所示,
设双曲线的右焦点为H,连接PH,由双曲线的性质,可知O为FH的中点,押题精练12由双曲线的定义,可知|PF|-|PH|=2a(P在双曲线的右支上),因为直线l与圆相切,所以PF⊥OE.又OE∥PH,所以PF⊥PH.押题精练12在△PFH中,|FH|2=|PH|2+|PF|2,押题精练12押题精练12解 设点P的坐标为(x0,y0),y0≠0.押题精练12证明 方法一 依题意,直线OP的方程为y=kx,由|AP|=|OA|,A(-a,0)及y0=kx0,押题精练12又a>b>0,故(1+k2)2>4k2+4,即k2+1>4,押题精练12方法二 依题意,直线OP的方程为y=kx,
可设点P的坐标为(x0,kx0).因为a>b>0,kx0≠0,押题精练12
同课章节目录
