【高考专辑】【专题27】2015年高三数学(理)【押题精练】排列、组合与二项式定理
文档属性
| 名称 | 【高考专辑】【专题27】2015年高三数学(理)【押题精练】排列、组合与二项式定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 00:00:00 | ||
图片预览










文档简介
课件52张PPT。专题27
排列、组合与二项式定理排列、组合与二项式定理主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.分类加法计数原理和分步乘法计数原理
如果每种方法都能将规定的事件完成,则要用分类加法计数原理将方法种数相加;如果需要通过若干步才能将规定的事件完成,则要用分步乘法计数原理将各步的方法种数相乘.2.排列与组合
(1)排列:从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.从n个不同元素中取出m个元素的排列数公式是A =n(n-1)(n-2)…(n-m+1)或写成
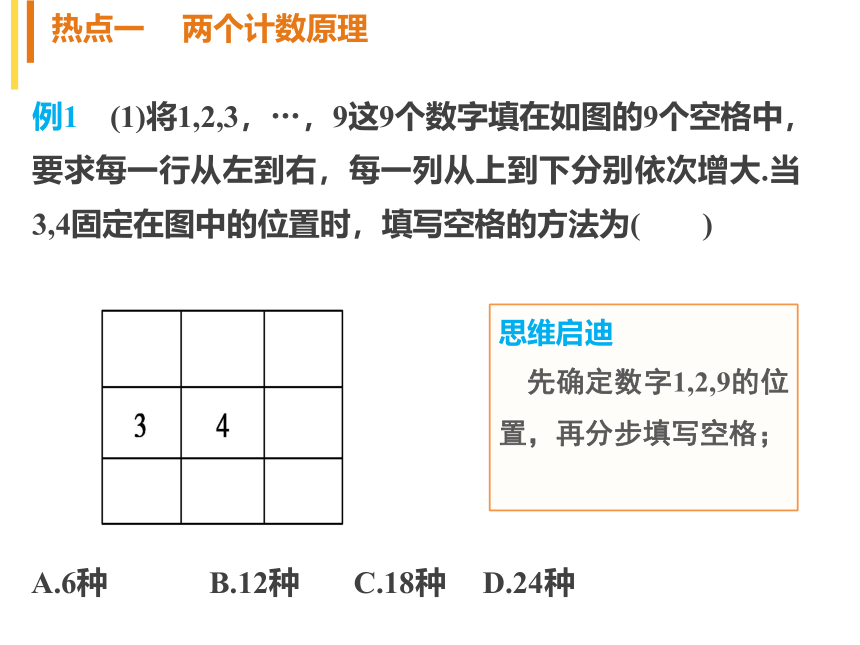
A = .(2)组合:从n个不同元素中取出m(m≤n)个元素组成一组,叫做从n个不同元素中取出m个元素的一个组合.从n个不同元素中取出m个元素的组合数公式是(3)组合数的性质热点一 两个计数原理热点二 排列与组合热点三 二项式定理热点分类突破例1 (1)将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为( )热点一 两个计数原理A.6种 B.12种 C.18种 D.24种思维启迪
先确定数字1,2,9的位置,再分步填写空格;解析 ∵每一行从左到右,每一列从上到下分别依次增大,1,2,9只有一种填法,5只能填在右上角或左下角,5填后与之相邻的空格可填6,7,8任一个;
余下两个数字按从小到大只有一种方法.
共有2×3=6种结果,故选A.
答案 A(2)如果一个三位正整数“a1a2a3”满足a1A.240 B.204
C.729 D.920思维启迪
按中间数进行分类.解析 分8类,当中间数为2时,有1×2=2种;
当中间数为3时,有2×3=6种;
当中间数为4时,有3×4=12种;
当中间数为5时,有4×5=20种;
当中间数为6时,有5×6=30种;
当中间数为7时,有6×7=42种;当中间数为8时,有7×8=56种;
当中间数为9时,有8×9=72种.
故共有2+6+12+20+30+42+56+72=240种.
答案 A变式训练1(1)(2014·大纲全国)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
A.60种 B.70种 C.75种 D.150种C(2)已知函数f(x)=ln(x2+1)的值域为{0,1,2},则满足这样条件的函数的个数为( )
A.8 B.9
C.26 D.27解析 因为值域为{0,1,2}, 即ln(x2+1)=0?x=0,所以定义域取值即在这5个元素中选取,③当定义域中有5个元素时,有一种情况.
所以共有4+4+1=9(个)这样的函数.
答案 B例2 (1)(2014·重庆)某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
A.72 B.120
C.144 D.168热点二 排列与组合思维启迪
将不能相邻的节目插空安排;解析 先安排小品节目和相声节目,然后让歌舞节目去插空.安排小品节目和相声节目的顺序有三种:“小品1,小品2,相声”“小品1,相声,小品2”和“相声,小品1,小品2”.同理,第三种情况也有36种安排方法,故共有36+36+48=120(种)安排方法.
答案 B(2)数列{an}共有12项,其中a1=0,a5=2,a12=5,且|ak+1-ak|=1,k=1,2,3,…,11,则满足这种条件的不同数列的个数为( )
A.84 B.168
C.76 D.152思维启迪
考虑数列中项的增减变化次数.解析 ∵|ak+1-ak|=1,k=1,2,3,…,11,
∴前一项总比后一项大1或小1,a1到a5中4个变化必然有3升1减,a5到a12中必然有5升2减,是组合的问题,答案 A变式训练2 (1)在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有( )
A.24种 B.48种
C.96种 D.144种解析 首先安排A有2种方法;
第二步在剩余的5个位置选取相邻的两个排B,C,有4种排法,而B,C位置互换有2种方法;答案 C(2)从0,1,2,3,4中任取四个数字组成无重复数字的四位数,其中偶数的个数是________(用数字作答).解析 0,1,2,3,4中任取四个数字组成无重复数字的四位数,且为偶数,有两种情况:故共有四位偶数60个.60热点三 二项式定理思维启迪
利用通项公式求常数项;C(2)如果(1+x+x2)(x-a)5(a为实常数)的展开式中所有项的系数和为0,则展开式中含x4项的系数为________.思维启迪
可用赋值法求二项展开式所有项的系数和.解析 ∵令x=1得(1+x+x2)(x-a)5的展开式中所有项的系数和为(1+1+12)(1-a)5=0,
∴a=1,∴(1+x+x2)(x-a)5=(1+x+x2)(x-1)5
=(x3-1)(x-1)4=x3(x-1)4-(x-1)4,-5变式训练3令7-2r=-3,得r=5.答案 C(2)(2014·浙江)在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)等于( )
A.45 B.60 C.120 D.210所以f(3,0)+f(2,1)+f(1,2)+f(0,3)C1.排列、组合应用题的解题策略
(1)在解决具体问题时,首先必须弄清楚是“分类”还是“分步”,接着还要搞清楚“分类”或者“分步”的具体标准是什么.
(2)区分某一问题是排列问题还是组合问题,关键看选出的元素与顺序是否有关.若交换某两个元素的位置对结果产生影响,则是排列问题;若交换任意两个元素的位置对结果没有影响,则是组合问题.也就是说排列本讲规律总结问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.
(3)排列、组合综合应用问题的常见解法:①特殊元素(特殊位置)优先安排法;②合理分类与准确分步;③排列、组合混合问题先选后排法;④相邻问题捆绑法;⑤不相邻问题插空法;⑥定序问题倍缩法;⑦多排问题一排法;⑧“小集团”问题先整体后局部法;⑨构造模型法;⑩正难则反、等价转化法.2.二项式定理是一个恒等式,对待恒等式通常有两种思路
一是利用恒等定理(两个多项式恒等,则对应项系数相等);二是赋值.这两种思路相结合可以使得二项展开式的系数问题迎刃而解.
另外,通项公式主要用于求二项式的指数,求满足条件的项或系数,求展开式的某一项或系数,在运用公式时要注意以下几点:(3)求展开式的特殊项,通常都是由题意列方程求出r,再求出所需的某项;有时需先求n,计算时要注意n和r的取值范围及它们之间的大小关系.真题感悟押题精练真题与押题12真题感悟1.(2014·浙江)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种(用数字作答).解析 把8张奖券分4组有两种分法,一种是分(一等奖,无奖)、(二等奖,无奖)、(三等奖,无奖)、(无奖,无奖)四组,分给4人有A种分法;12真题感悟答案 60真题感悟212押题精练1231.给一个正方体的六个面涂上4种不同的颜色(红、黄、绿、蓝),要求相邻2个面涂不同的颜色,则所有涂色方法的种数为( )
A.6 B.12 C.24 D.484解析 由于涂色过程中,要使用4种颜色,且相邻的面不同色,
对于正方体的3组对面来说,必然有2组对面同色,1组对面不同色,而且3组对面具有“地位对等性”,因此,只需从4种颜色中选择2种涂在其中2组对面上,剩下的2种颜色分别涂在另外2个面上即可.答案 A押题精练12342.某电视台一节目收视率很高,现要连续插播4个广告,其中2个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是商业广告,且2个商业广告不能连续播放,则不同的播放方式有( )
A.8种 B.16种 C.18种 D.24种押题精练1234答案 A押题精练1234押题精练1234解析 根据二项式系数的性质,得2n=10,答案 C押题精练1234押题精练1234令x=0,可得a0=1.答案 C押题精练1234
排列、组合与二项式定理排列、组合与二项式定理主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.分类加法计数原理和分步乘法计数原理
如果每种方法都能将规定的事件完成,则要用分类加法计数原理将方法种数相加;如果需要通过若干步才能将规定的事件完成,则要用分步乘法计数原理将各步的方法种数相乘.2.排列与组合
(1)排列:从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.从n个不同元素中取出m个元素的排列数公式是A =n(n-1)(n-2)…(n-m+1)或写成
A = .(2)组合:从n个不同元素中取出m(m≤n)个元素组成一组,叫做从n个不同元素中取出m个元素的一个组合.从n个不同元素中取出m个元素的组合数公式是(3)组合数的性质热点一 两个计数原理热点二 排列与组合热点三 二项式定理热点分类突破例1 (1)将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为( )热点一 两个计数原理A.6种 B.12种 C.18种 D.24种思维启迪
先确定数字1,2,9的位置,再分步填写空格;解析 ∵每一行从左到右,每一列从上到下分别依次增大,1,2,9只有一种填法,5只能填在右上角或左下角,5填后与之相邻的空格可填6,7,8任一个;
余下两个数字按从小到大只有一种方法.
共有2×3=6种结果,故选A.
答案 A(2)如果一个三位正整数“a1a2a3”满足a1
C.729 D.920思维启迪
按中间数进行分类.解析 分8类,当中间数为2时,有1×2=2种;
当中间数为3时,有2×3=6种;
当中间数为4时,有3×4=12种;
当中间数为5时,有4×5=20种;
当中间数为6时,有5×6=30种;
当中间数为7时,有6×7=42种;当中间数为8时,有7×8=56种;
当中间数为9时,有8×9=72种.
故共有2+6+12+20+30+42+56+72=240种.
答案 A变式训练1(1)(2014·大纲全国)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
A.60种 B.70种 C.75种 D.150种C(2)已知函数f(x)=ln(x2+1)的值域为{0,1,2},则满足这样条件的函数的个数为( )
A.8 B.9
C.26 D.27解析 因为值域为{0,1,2}, 即ln(x2+1)=0?x=0,所以定义域取值即在这5个元素中选取,③当定义域中有5个元素时,有一种情况.
所以共有4+4+1=9(个)这样的函数.
答案 B例2 (1)(2014·重庆)某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
A.72 B.120
C.144 D.168热点二 排列与组合思维启迪
将不能相邻的节目插空安排;解析 先安排小品节目和相声节目,然后让歌舞节目去插空.安排小品节目和相声节目的顺序有三种:“小品1,小品2,相声”“小品1,相声,小品2”和“相声,小品1,小品2”.同理,第三种情况也有36种安排方法,故共有36+36+48=120(种)安排方法.
答案 B(2)数列{an}共有12项,其中a1=0,a5=2,a12=5,且|ak+1-ak|=1,k=1,2,3,…,11,则满足这种条件的不同数列的个数为( )
A.84 B.168
C.76 D.152思维启迪
考虑数列中项的增减变化次数.解析 ∵|ak+1-ak|=1,k=1,2,3,…,11,
∴前一项总比后一项大1或小1,a1到a5中4个变化必然有3升1减,a5到a12中必然有5升2减,是组合的问题,答案 A变式训练2 (1)在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有( )
A.24种 B.48种
C.96种 D.144种解析 首先安排A有2种方法;
第二步在剩余的5个位置选取相邻的两个排B,C,有4种排法,而B,C位置互换有2种方法;答案 C(2)从0,1,2,3,4中任取四个数字组成无重复数字的四位数,其中偶数的个数是________(用数字作答).解析 0,1,2,3,4中任取四个数字组成无重复数字的四位数,且为偶数,有两种情况:故共有四位偶数60个.60热点三 二项式定理思维启迪
利用通项公式求常数项;C(2)如果(1+x+x2)(x-a)5(a为实常数)的展开式中所有项的系数和为0,则展开式中含x4项的系数为________.思维启迪
可用赋值法求二项展开式所有项的系数和.解析 ∵令x=1得(1+x+x2)(x-a)5的展开式中所有项的系数和为(1+1+12)(1-a)5=0,
∴a=1,∴(1+x+x2)(x-a)5=(1+x+x2)(x-1)5
=(x3-1)(x-1)4=x3(x-1)4-(x-1)4,-5变式训练3令7-2r=-3,得r=5.答案 C(2)(2014·浙江)在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)等于( )
A.45 B.60 C.120 D.210所以f(3,0)+f(2,1)+f(1,2)+f(0,3)C1.排列、组合应用题的解题策略
(1)在解决具体问题时,首先必须弄清楚是“分类”还是“分步”,接着还要搞清楚“分类”或者“分步”的具体标准是什么.
(2)区分某一问题是排列问题还是组合问题,关键看选出的元素与顺序是否有关.若交换某两个元素的位置对结果产生影响,则是排列问题;若交换任意两个元素的位置对结果没有影响,则是组合问题.也就是说排列本讲规律总结问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.
(3)排列、组合综合应用问题的常见解法:①特殊元素(特殊位置)优先安排法;②合理分类与准确分步;③排列、组合混合问题先选后排法;④相邻问题捆绑法;⑤不相邻问题插空法;⑥定序问题倍缩法;⑦多排问题一排法;⑧“小集团”问题先整体后局部法;⑨构造模型法;⑩正难则反、等价转化法.2.二项式定理是一个恒等式,对待恒等式通常有两种思路
一是利用恒等定理(两个多项式恒等,则对应项系数相等);二是赋值.这两种思路相结合可以使得二项展开式的系数问题迎刃而解.
另外,通项公式主要用于求二项式的指数,求满足条件的项或系数,求展开式的某一项或系数,在运用公式时要注意以下几点:(3)求展开式的特殊项,通常都是由题意列方程求出r,再求出所需的某项;有时需先求n,计算时要注意n和r的取值范围及它们之间的大小关系.真题感悟押题精练真题与押题12真题感悟1.(2014·浙江)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种(用数字作答).解析 把8张奖券分4组有两种分法,一种是分(一等奖,无奖)、(二等奖,无奖)、(三等奖,无奖)、(无奖,无奖)四组,分给4人有A种分法;12真题感悟答案 60真题感悟212押题精练1231.给一个正方体的六个面涂上4种不同的颜色(红、黄、绿、蓝),要求相邻2个面涂不同的颜色,则所有涂色方法的种数为( )
A.6 B.12 C.24 D.484解析 由于涂色过程中,要使用4种颜色,且相邻的面不同色,
对于正方体的3组对面来说,必然有2组对面同色,1组对面不同色,而且3组对面具有“地位对等性”,因此,只需从4种颜色中选择2种涂在其中2组对面上,剩下的2种颜色分别涂在另外2个面上即可.答案 A押题精练12342.某电视台一节目收视率很高,现要连续插播4个广告,其中2个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是商业广告,且2个商业广告不能连续播放,则不同的播放方式有( )
A.8种 B.16种 C.18种 D.24种押题精练1234答案 A押题精练1234押题精练1234解析 根据二项式系数的性质,得2n=10,答案 C押题精练1234押题精练1234令x=0,可得a0=1.答案 C押题精练1234
同课章节目录
