【高考专辑】【专题29】2015年高三数学(理)【押题精练】统计与统计案例
文档属性
| 名称 | 【高考专辑】【专题29】2015年高三数学(理)【押题精练】统计与统计案例 |  | |
| 格式 | zip | ||
| 文件大小 | 512.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 19:06:49 | ||
图片预览






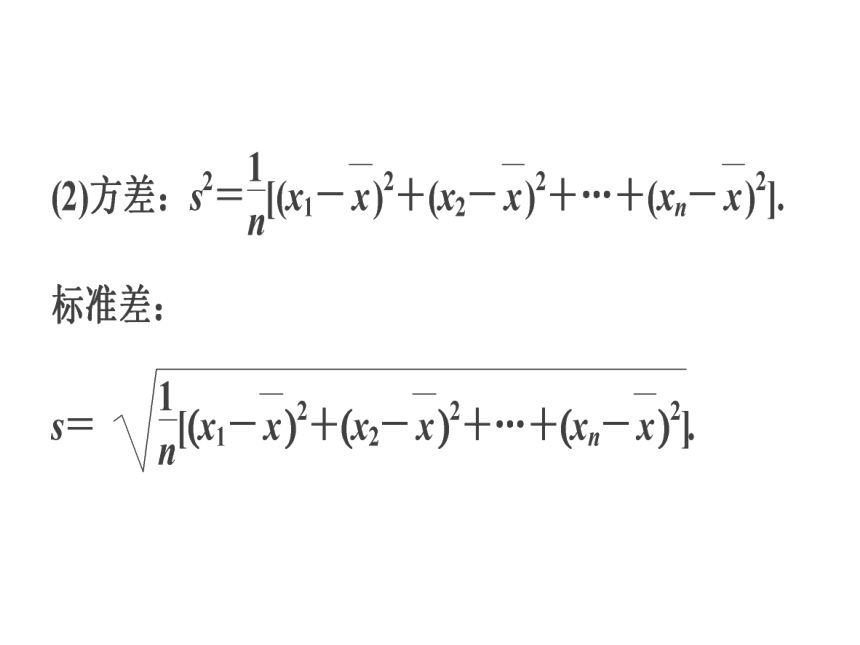




文档简介
课件62张PPT。专题29
统计与统计案例统计与统计案例主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题1主干知识梳理1.随机抽样
(1)简单随机抽样特点是从总体中逐个抽取.适用范围:总体中的个体较少.
(2)系统抽样特点是将总体均分成几部分,按事先确定的规则在各部分中抽取.适用范围:总体中的个体数较多.
(3)分层抽样特点是将总体分成几层,分层进行抽取.适用范围:总体由差异明显的几部分组成.2.常用的统计图表
(1)频率分布直方图②各小长方形的面积之和等于1;(2)茎叶图
在样本数据较少时,用茎叶图表示数据的效果较好.
3.用样本的数字特征估计总体的数字特征
(1)众数、中位数、平均数4.变量的相关性与最小二乘法
(1)相关关系的概念、正相关和负相关、相关系数.5.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是热点一 抽样方法热点二 用样本估计总体热点三 统计案例热点分类突破例1 (1)(2013·陕西)某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为( )
A.11 B.12 C.13 D.14热点一 抽样方法思维启迪
系统抽样时需要抽取几个个体,样本就分成几组,且抽取号码的间隔相同;答案 B(2)某学校共有师生3 200人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是________.思维启迪
分层抽样最重要的是各层的比例.解析 本题属于分层抽样,设该学校的教师人数为x,200变式训练1(1)某校高一、高二、高三分别有学生人数为495,493,482,现采用系统抽样方法,抽取49人做问卷调查,将高一、高二、高三学生依次随机按1,2,3,…,1 470编号,若第1组有简单随机抽样方法抽取的号码为23,则高二应抽取的学生人数为( )
A.15 B.16 C.17 D.18解析 由系统抽样方法,知按编号依次每30个编号作为一组,共分49组,
高二学生的编号为496到988,在第17组到第33组内,第17组抽取的编号为16×30+23=503,为高二学生,第33组抽取的编号为32×30+23=983,为高二学生,
故共抽取高二学生人数为33-16=17,故选C.
答案 C(2)(2014·广东)已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )A.200,20 B.100,20
C.200,10 D.100,10解析 该地区中、小学生总人数为
3 500+2 000+4 500=10 000,
则样本容量为10 000×2%=200,
其中抽取的高中生近视人数为
2 000×2%×50%=20,故选A.
答案 A例2 (1)(2014·山东)为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,热点二 用样本估计总体第三组中没有疗效的有6人,则第三组中有疗效的人数为( )思维启迪
根据第一组与第二组的人数和对应频率估计样本总数,然后利用第三组的频率和无疗效人数计算;A.6 B.8 C.12 D.18所以第三组人数为50×0.36=18,
有疗效的人数为18-6=12.
答案 C(2)PM2.5是指大气中直径小于或等于
2.5微米的颗粒物,也称为可入肺颗
粒物,如图是根据某地某日早7点至
晚8点甲、乙两个PM2.5监测点统计的
数据(单位:毫克/每立方米)列出的茎
叶图,则甲、乙两地浓度的方差较小的是( )
A.甲 B.乙
C.甲乙相等 D.无法确定思维启迪
直接根据公式计算方差.所以甲、乙两地浓度的方差较小的是甲地.
答案 A变式训练2 (1)某商场在庆元宵促销活动中,对
元宵节9时至14时的销售额进行统
计,其频率分布直方图如图所示,
已知9时至10时的销售额为2.5万
元,则11时至12时的销售额为____
万元.所以x=10.10(2)(2014·陕西)设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
A.1+a,4 B.1+a,4+a
C.1,4 D.1,4+a所以y1,y2,…,y10的均值为1+a,方差不变仍为4.
故选A.A例3 (1)以下是某年2月某地区搜集到的新房屋的销售价格y和房屋的面积x的数据.热点三 统计案例答案 31.244 2(2)(2014·江西)某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )表1表2表3表4A.成绩 B.视力 C.智商 D.阅读量思维启迪
根据列联表,计算K2的值解析 A中,a=6,b=14,c=10,d=22,a+b=20,c+d=32,a+c=16,b+d=36,n=52,B中,a=4,b=16,c=12,d=20,a+b=20,c+d=32,a+c=16,b+d=36,n=52,C中,a=8,b=12,c=8,d=24,a+b=20,c+d=32,a+c=16,b+d=36,n=52,D中,a=14,b=6,c=2,d=30,a+b=20,c+d=32,a+c=16,b+d=36,n=52,∴与性别有关联的可能性最大的变量是阅读量.
答案 D变式训练3(1)已知x、y取值如下表:A.1.30 B.1.45 C.1.65 D.1.80答案 B(2)某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.得以下2×2列联表:则在犯错误的概率不超过________的前提下认为人的脚的大小与身高之间有关系.而K2>6.635的概率约为0.01,所以在犯错误的概率不超过0.01的前提下认为人的脚的大小与身高之间有关系.0.011.随机抽样的方法有三种,其中简单随机抽样适用于总体中的个体数量不多的情况,当总体中的个体数量明显较多时要使用系统抽样,当总体中的个体具有明显的层次时使用分层抽样.系统抽样最重要的特征是“等距”,分层抽样,最重要的是各层的“比例”.本讲规律总结2.用样本估计总体
(1)在频率分布直方图中,各小长方形的面积表示相应的频率,各小长方形的面积的和为1.
(2)众数、中位数及平均数的异同:众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量.真题感悟押题精练真题与押题12真题感悟1.(2014·江苏)为了了解一片经济
林的生长情况,随机抽测了其中
60株树木的底部周长(单位:cm),
所得数据均在区间[80,130]上,其
频率分布直方图如图所示,则在抽测的60株树木中,有________株树木的底部周长小于100 cm.12真题感悟解析 底部周长在[80,90)的频率为0.015×10=0.15,
底部周长在[90,100)的频率为0.025×10=0.25,
样本容量为60,所以树木的底部周长小于100 cm的株数为(0.15+0.25)×60=24.
答案 24真题感悟21真题感悟21解析 因为变量x和y正相关,则回归直线的斜率为正,故可以排除选项C和D.
因为样本点的中心在回归直线上,把点(3,3.5)的坐标分别代入选项A和B中的线性回归方程进行检验,可以排除B,故选A.
答案 A1.某地区对某路段公路上行驶的汽
车速度实施监控,从中抽取50辆汽
车进行测速分析,得到如图所示的
时速的频率分布直方图,根据该图,
时速在70 km/h以下的汽车有___辆.解析 时速在70 km/h以下的汽车所占的频率为0.01×10+0.03×10=0.4,共有0.4×50=20(辆).20押题精练12342.某教育出版社在高三期末考试结束后,从某市参与考试的考生中选取600名学生对在此期间购买教辅资料的情况进行调研,得到如下数据:押题精练1234若该教育出版社计划用分层抽样的方法从这600人中随机抽取60人进行座谈,则只买试题类的学生应抽取的人数为________.24押题精练12343.下表提供了某厂节能减排技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据:押题精练1234根据上表提供的数据,求出y关于x的线性回归方程为 =0.7x+0.35,那么表中t的值为________.3押题精练12344.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:押题精练1234附:押题精练1234参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别无关”押题精练1234C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”押题精练1234解析 由公式可计算K2的观测值k所以有90%以上的把握认为“该市民能否做到‘光盘’与性别有关”,故选C.
答案 C押题精练1234
统计与统计案例统计与统计案例主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题1主干知识梳理1.随机抽样
(1)简单随机抽样特点是从总体中逐个抽取.适用范围:总体中的个体较少.
(2)系统抽样特点是将总体均分成几部分,按事先确定的规则在各部分中抽取.适用范围:总体中的个体数较多.
(3)分层抽样特点是将总体分成几层,分层进行抽取.适用范围:总体由差异明显的几部分组成.2.常用的统计图表
(1)频率分布直方图②各小长方形的面积之和等于1;(2)茎叶图
在样本数据较少时,用茎叶图表示数据的效果较好.
3.用样本的数字特征估计总体的数字特征
(1)众数、中位数、平均数4.变量的相关性与最小二乘法
(1)相关关系的概念、正相关和负相关、相关系数.5.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是热点一 抽样方法热点二 用样本估计总体热点三 统计案例热点分类突破例1 (1)(2013·陕西)某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为( )
A.11 B.12 C.13 D.14热点一 抽样方法思维启迪
系统抽样时需要抽取几个个体,样本就分成几组,且抽取号码的间隔相同;答案 B(2)某学校共有师生3 200人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是________.思维启迪
分层抽样最重要的是各层的比例.解析 本题属于分层抽样,设该学校的教师人数为x,200变式训练1(1)某校高一、高二、高三分别有学生人数为495,493,482,现采用系统抽样方法,抽取49人做问卷调查,将高一、高二、高三学生依次随机按1,2,3,…,1 470编号,若第1组有简单随机抽样方法抽取的号码为23,则高二应抽取的学生人数为( )
A.15 B.16 C.17 D.18解析 由系统抽样方法,知按编号依次每30个编号作为一组,共分49组,
高二学生的编号为496到988,在第17组到第33组内,第17组抽取的编号为16×30+23=503,为高二学生,第33组抽取的编号为32×30+23=983,为高二学生,
故共抽取高二学生人数为33-16=17,故选C.
答案 C(2)(2014·广东)已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )A.200,20 B.100,20
C.200,10 D.100,10解析 该地区中、小学生总人数为
3 500+2 000+4 500=10 000,
则样本容量为10 000×2%=200,
其中抽取的高中生近视人数为
2 000×2%×50%=20,故选A.
答案 A例2 (1)(2014·山东)为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,热点二 用样本估计总体第三组中没有疗效的有6人,则第三组中有疗效的人数为( )思维启迪
根据第一组与第二组的人数和对应频率估计样本总数,然后利用第三组的频率和无疗效人数计算;A.6 B.8 C.12 D.18所以第三组人数为50×0.36=18,
有疗效的人数为18-6=12.
答案 C(2)PM2.5是指大气中直径小于或等于
2.5微米的颗粒物,也称为可入肺颗
粒物,如图是根据某地某日早7点至
晚8点甲、乙两个PM2.5监测点统计的
数据(单位:毫克/每立方米)列出的茎
叶图,则甲、乙两地浓度的方差较小的是( )
A.甲 B.乙
C.甲乙相等 D.无法确定思维启迪
直接根据公式计算方差.所以甲、乙两地浓度的方差较小的是甲地.
答案 A变式训练2 (1)某商场在庆元宵促销活动中,对
元宵节9时至14时的销售额进行统
计,其频率分布直方图如图所示,
已知9时至10时的销售额为2.5万
元,则11时至12时的销售额为____
万元.所以x=10.10(2)(2014·陕西)设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
A.1+a,4 B.1+a,4+a
C.1,4 D.1,4+a所以y1,y2,…,y10的均值为1+a,方差不变仍为4.
故选A.A例3 (1)以下是某年2月某地区搜集到的新房屋的销售价格y和房屋的面积x的数据.热点三 统计案例答案 31.244 2(2)(2014·江西)某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )表1表2表3表4A.成绩 B.视力 C.智商 D.阅读量思维启迪
根据列联表,计算K2的值解析 A中,a=6,b=14,c=10,d=22,a+b=20,c+d=32,a+c=16,b+d=36,n=52,B中,a=4,b=16,c=12,d=20,a+b=20,c+d=32,a+c=16,b+d=36,n=52,C中,a=8,b=12,c=8,d=24,a+b=20,c+d=32,a+c=16,b+d=36,n=52,D中,a=14,b=6,c=2,d=30,a+b=20,c+d=32,a+c=16,b+d=36,n=52,∴与性别有关联的可能性最大的变量是阅读量.
答案 D变式训练3(1)已知x、y取值如下表:A.1.30 B.1.45 C.1.65 D.1.80答案 B(2)某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.得以下2×2列联表:则在犯错误的概率不超过________的前提下认为人的脚的大小与身高之间有关系.而K2>6.635的概率约为0.01,所以在犯错误的概率不超过0.01的前提下认为人的脚的大小与身高之间有关系.0.011.随机抽样的方法有三种,其中简单随机抽样适用于总体中的个体数量不多的情况,当总体中的个体数量明显较多时要使用系统抽样,当总体中的个体具有明显的层次时使用分层抽样.系统抽样最重要的特征是“等距”,分层抽样,最重要的是各层的“比例”.本讲规律总结2.用样本估计总体
(1)在频率分布直方图中,各小长方形的面积表示相应的频率,各小长方形的面积的和为1.
(2)众数、中位数及平均数的异同:众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量.真题感悟押题精练真题与押题12真题感悟1.(2014·江苏)为了了解一片经济
林的生长情况,随机抽测了其中
60株树木的底部周长(单位:cm),
所得数据均在区间[80,130]上,其
频率分布直方图如图所示,则在抽测的60株树木中,有________株树木的底部周长小于100 cm.12真题感悟解析 底部周长在[80,90)的频率为0.015×10=0.15,
底部周长在[90,100)的频率为0.025×10=0.25,
样本容量为60,所以树木的底部周长小于100 cm的株数为(0.15+0.25)×60=24.
答案 24真题感悟21真题感悟21解析 因为变量x和y正相关,则回归直线的斜率为正,故可以排除选项C和D.
因为样本点的中心在回归直线上,把点(3,3.5)的坐标分别代入选项A和B中的线性回归方程进行检验,可以排除B,故选A.
答案 A1.某地区对某路段公路上行驶的汽
车速度实施监控,从中抽取50辆汽
车进行测速分析,得到如图所示的
时速的频率分布直方图,根据该图,
时速在70 km/h以下的汽车有___辆.解析 时速在70 km/h以下的汽车所占的频率为0.01×10+0.03×10=0.4,共有0.4×50=20(辆).20押题精练12342.某教育出版社在高三期末考试结束后,从某市参与考试的考生中选取600名学生对在此期间购买教辅资料的情况进行调研,得到如下数据:押题精练1234若该教育出版社计划用分层抽样的方法从这600人中随机抽取60人进行座谈,则只买试题类的学生应抽取的人数为________.24押题精练12343.下表提供了某厂节能减排技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据:押题精练1234根据上表提供的数据,求出y关于x的线性回归方程为 =0.7x+0.35,那么表中t的值为________.3押题精练12344.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:押题精练1234附:押题精练1234参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别无关”押题精练1234C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”押题精练1234解析 由公式可计算K2的观测值k所以有90%以上的把握认为“该市民能否做到‘光盘’与性别有关”,故选C.
答案 C押题精练1234
同课章节目录
