【高考专辑】【专题30】2015年高三数学(理)【押题精练】数形结合思想
文档属性
| 名称 | 【高考专辑】【专题30】2015年高三数学(理)【押题精练】数形结合思想 |

|
|
| 格式 | zip | ||
| 文件大小 | 602.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 00:00:00 | ||
图片预览










文档简介
课件59张PPT。专题30
数形结合思想数形结合思想思 想 方 法 概 述热 点 分 类 突 破真 题 与 押 题3思想方法概述1.数形结合的数学思想:包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.2.运用数形结合思想分析解决问题时,要遵循三个原则:
(1)等价性原则.在数形结合时,代数性质和几何性质的转换必须是等价的,否则解题将会出现漏洞.有时,由于图形的局限性,不能完整的表现数的一般性,这时图形的性质只能是一种直观而浅显的说明,要注意其带来的负面效应.
(2)双方性原则.既要进行几何直观分析,又要进行相应的代数抽象探求,仅对代数问题进行几何分析容易出错.(3)简单性原则.不要为了“数形结合”而数形结合.具体运用时,一要考虑是否可行和是否有利;二要选择好突破口,恰当设参、用参、建立关系、做好转化;三要挖掘隐含条件,准确界定参变量的取值范围,特别是运用函数图象时应设法选择动直线与定二次曲线.3.数形结合思想解决的问题常有以下几种:
(1)构建函数模型并结合其图象求参数的取值范围.
(2)构建函数模型并结合其图象研究方程根的范围.
(3)构建函数模型并结合其图象研究量与量之间的大小关系.
(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式.(5)构建立体几何模型研究代数问题.
(6)构建解析几何中的斜率、截距、距离等模型研究最值问题.
(7)构建方程模型,求根的个数.
(8)研究图形的形状、位置关系、性质等.4.数形结合思想是解答高考数学试题的一种常用方法与技巧,特别是在解选择题、填空题时发挥着奇特功效,这就要求我们在平时学习中加强这方面的训练,以提高解题能力和速度.具体操作时,应注意以下几点:
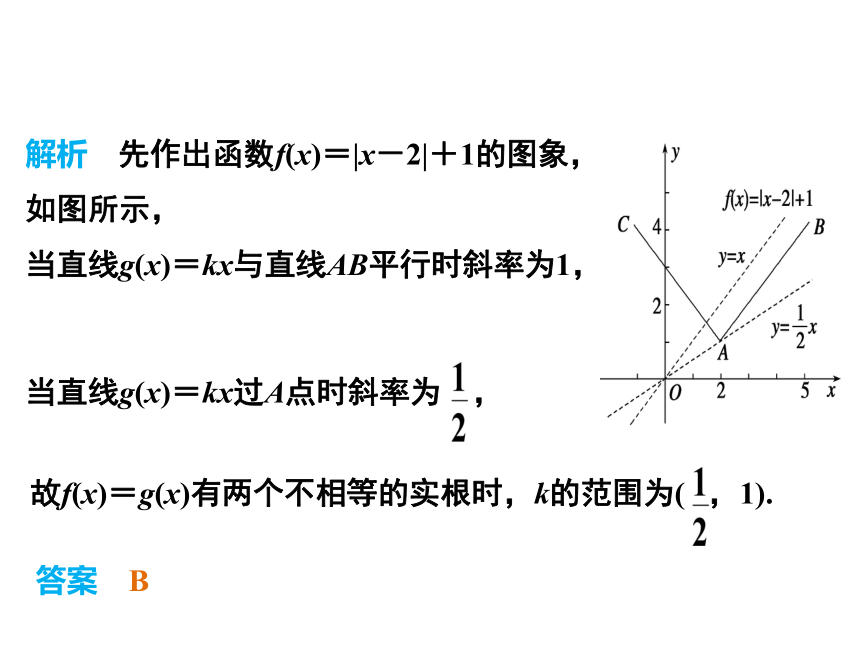
(1)准确画出函数图象,注意函数的定义域.(2)用图象法讨论方程(特别是含参数的方程)的解的个数是一种行之有效的方法,值得注意的是首先要把方程两边的代数式看作是两个函数的表达式(有时可能先作适当调整,以便于作图),然后作出两个函数的图象,由图求解.热点一 利用数形结合思想讨论方程的根热点二 利用数形结合思想解不等式、求参数范围热点三 利用数形结合思想解最值问题热点分类突破热点一 利用数形结合思想讨论方程的根解析 先作出函数f(x)=|x-2|+1的图象,
如图所示,
当直线g(x)=kx与直线AB平行时斜率为1,当直线g(x)=kx过A点时斜率为 ,故f(x)=g(x)有两个不相等的实根时,k的范围为( ,1).答案 B变式训练1解析 由f(-4)=f(0),f(-2)=-2,解得b=4,c=2,∴f(x)=作出函数y=f(x)及y=x的函数图象
如图所示,由图可得交点有3个.
答案 C例2 (1)已知奇函数f(x)的定义域是{x|x≠0,x∈R},且在(0,+∞)上单调递增,若f(1)=0,则满足x·f(x)<0的x的取值范围是____________.热点二 利用数形结合思想解不等式、求参数范围由图可知x·f(x)<0的x的取值范围是
(-1,0)∪(0,1).解析 作出符合条件的一个函数图象
草图即可,(-1,0)∪(0,1)(2)若不等式|x-2a|≥ x+a-1对x∈R恒成立,则a的取值范围是________.解析 作出y=|x-2a|和y= x+a-1的简图,依题意知应有2a≤2-2a,故a≤ .变式训练2 (1)设A={(x,y)|x2+(y-1)2=1},B={(x,y)|x+y+m≥0},则使A?B成立的实数m的取值范围是_______.解析 集合A是一个圆x2+(y-1)2=1上的点的集合,
集合B是一个不等式x+y+m≥0表示的平面区域内的点的集合,要使A?B,则应使圆被平面区域所包含
(如图),即直线x+y+m=0应与圆相切或相离
(在圆的下方),例3 (1)已知P是直线l:3x+4y+8=0上的动点,PA、PB是圆x2+y2-2x-2y+1=0的两条切线,A、B是切点,C是圆心,则四边形PACB面积的最小值为________.热点三 利用数形结合思想解最值问题解析 从运动的观点看问题,当动点P沿
直线3x+4y+8=0向左上方或右下方无穷
远处运动时,当点P从左上、右下两个方向向中间运动时,S四边形PACB变小,
显然,当点P到达一个最特殊的位置,即CP垂直直线l时,S四边形PACB应有唯一的最小值,解析 画出可行域如图,所求的x2+y2-
6x+9=(x-3)2+y2是点Q(3,0)到可行域上
的点的距离的平方,由图形知最小值为Q到射线x-y-1=0
(x≥0)的距离d的平方,最大值为|QA|2=16.∴取值范围是[2,16].
答案 B变式训练3(1)(2013·重庆)设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
A.6 B.4 C.3 D.2解析 由题意,知圆的圆心坐标为(3,-1),圆的半径长为2,
|PQ|的最小值为圆心到直线x=-3的距离减去圆的半径长,
所以|PQ|min=3-(-3)-2=4.故选B.B又 的几何意义是可行域内的点与坐标原点
连线的斜率k.解析 可行域如图所示.由图知,过点A的直线OA的斜率最小.答案 21.在数学中函数的图象、方程的曲线、不等式所表示的平面区域、向量的几何意义、复数的几何意义等都实现以形助数的途径,当试题中涉及这些问题的数量关系时,我们可以通过图形分析这些数量关系,达到解题的目的.本讲规律总结2.有些图形问题,单纯从图形上无法看出问题的结论,这就要对图形进行数量上的分析,通过数的帮助达到解题的目的.
3.利用数形结合解题,有时只需把图象大致形状画出即可,不需要精确图象.4.数形结合思想常用模型:一次、二次函数图象;斜率公式;两点间的距离公式(或向量的模、复数的模);点到直线的距离公式等.真题感悟押题精练真题与押题12真题感悟34解析 设P(x,0),设C1(2,3)关于x轴的对称点为C1′(2,-3),12真题感悟34答案 A12真题感悟34解析 ∵∠AOB=90°,∴点O在圆C上.
设直线2x+y-4=0与圆C相切于点D,
则点C与点O间的距离等于它到直线2x+y-4=0的距离,
∴点C在以O为焦点,以直线2x+y-4=0为准线的抛物线上,
∴当且仅当O,C,D共线时,圆的直径最小为|OD|.12真题感悟3412真题感悟34答案 A12真题感悟34解析 函数y=|f(x)|的图象如图.
①当a=0时,|f(x)|≥ax显然成立.
②当a>0时,只需在x>0时,
ln(x+1)≥ax成立.
比较对数函数与一次函数y=ax的增长速度.
显然不存在a>0使ln(x+1)≥ax在x>0上恒成立.12真题感悟34③当a<0时,只需在x<0时,x2-2x≥ax成立.
即a≥x-2成立,所以a≥-2.
综上所述:-2≤a≤0.故选D.
答案 D12真题感悟344.(2014·天津)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________.12真题感悟34解析 设y1=f(x)=|x2+3x|,y2=a|x-1|,在同一直角坐标系中作出y1=|x2+3x|,
y2=a|x-1|的图象如图所示.由图可知f(x)-a|x-1|=0有4个互异的实数根等价于y1=|x2+3x|与y2=a|x-1|的图象有4个不同的交点.当4个交点横坐标都小于1时,12真题感悟34消y得x2+(3-a)x+a=0,故Δ=a2-10a+9>0,
且x1+x2=a-3<2,x1x2=a<1,联立可得00,
且x3+x4=a-3>2,x3x4=a>1,联立可得a>9,
综上知,09.
答案 (0,1)∪(9,+∞)押题精练1231.方程|x2-2x|=a2+1(a>0)的解的个数是( )
A.1 B.2 C.3 D.4456解析 (数形结合法)
∵a>0,∴a2+1>1.∴y=|x2-2x|的图象与y=a2+1的图象总有两个交点.而y=|x2-2x|的图象如图,B2.不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.(-∞,-1]∪[4,+∞)
B.(-∞,-2]∪[5,+∞)
C.[1,2]
D.(-∞,1]∪[2,+∞)押题精练123456押题精练123456画出函数f(x)的图象,如图,可以看出函数f(x)的最大值为4,
故只要a2-3a≥4即可,
解得a≤-1或a≥4.正确选项为A.答案 A3.经过P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的斜率k和倾斜角α的取值范围分别为________,________.押题精练123456解析 如图所示,结合图形:为使l与
线段AB总有公共点,则kPA≤k≤kPB,而kPB>0,kPA<0,押题精练123456故k<0时,倾斜角α为钝角,k=0时,α=0,k>0时,α为锐角.押题精练123456押题精练123456押题精练123456解析 由题意知原点O到直线x+y-2=0的距离为|OM|的最小值.押题精练123456押题精练1234566.设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;押题精练123456解 函数g(x)=bx2-ln x的定义域为(0,+∞),
f′(x)=3ax2-3a?f′(1)=0,g′(x)=2bx- ?g′(1)=2b-1,依题意得2b-1=0,所以b= .押题精练123456押题精练123456即g(x)在(1,+∞)上单调递增,当a=0时,方程F(x)=a2不可能有四个解;
当a<0,x∈(-∞,-1)时,f′(x)<0,
即f(x)在(-∞,-1)上单调递减,x∈(-1,0)时,f′(x)>0,
即f(x)在(-1,0)上单调递增,
所以当x=-1时,f(x)取得极小值f(-1)=2a,押题精练123456又f(0)=0,所以F(x)的图象如图(1)所示,从图象可以看出F(x)=a2不可能有四个解.
当a>0,x∈(-∞,-1)时,f′(x)>0,
即f(x)在(-∞,-1)上单调递增,x∈(-1,0)时,f′(x)<0,
即f(x)在(-1,0)上单调递减,
所以当x=-1时,f(x)取得极大值f(-1)=2a.押题精练123456又f(0)=0,所以F(x)的图象如图(2)所示,
数形结合思想数形结合思想思 想 方 法 概 述热 点 分 类 突 破真 题 与 押 题3思想方法概述1.数形结合的数学思想:包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.2.运用数形结合思想分析解决问题时,要遵循三个原则:
(1)等价性原则.在数形结合时,代数性质和几何性质的转换必须是等价的,否则解题将会出现漏洞.有时,由于图形的局限性,不能完整的表现数的一般性,这时图形的性质只能是一种直观而浅显的说明,要注意其带来的负面效应.
(2)双方性原则.既要进行几何直观分析,又要进行相应的代数抽象探求,仅对代数问题进行几何分析容易出错.(3)简单性原则.不要为了“数形结合”而数形结合.具体运用时,一要考虑是否可行和是否有利;二要选择好突破口,恰当设参、用参、建立关系、做好转化;三要挖掘隐含条件,准确界定参变量的取值范围,特别是运用函数图象时应设法选择动直线与定二次曲线.3.数形结合思想解决的问题常有以下几种:
(1)构建函数模型并结合其图象求参数的取值范围.
(2)构建函数模型并结合其图象研究方程根的范围.
(3)构建函数模型并结合其图象研究量与量之间的大小关系.
(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式.(5)构建立体几何模型研究代数问题.
(6)构建解析几何中的斜率、截距、距离等模型研究最值问题.
(7)构建方程模型,求根的个数.
(8)研究图形的形状、位置关系、性质等.4.数形结合思想是解答高考数学试题的一种常用方法与技巧,特别是在解选择题、填空题时发挥着奇特功效,这就要求我们在平时学习中加强这方面的训练,以提高解题能力和速度.具体操作时,应注意以下几点:
(1)准确画出函数图象,注意函数的定义域.(2)用图象法讨论方程(特别是含参数的方程)的解的个数是一种行之有效的方法,值得注意的是首先要把方程两边的代数式看作是两个函数的表达式(有时可能先作适当调整,以便于作图),然后作出两个函数的图象,由图求解.热点一 利用数形结合思想讨论方程的根热点二 利用数形结合思想解不等式、求参数范围热点三 利用数形结合思想解最值问题热点分类突破热点一 利用数形结合思想讨论方程的根解析 先作出函数f(x)=|x-2|+1的图象,
如图所示,
当直线g(x)=kx与直线AB平行时斜率为1,当直线g(x)=kx过A点时斜率为 ,故f(x)=g(x)有两个不相等的实根时,k的范围为( ,1).答案 B变式训练1解析 由f(-4)=f(0),f(-2)=-2,解得b=4,c=2,∴f(x)=作出函数y=f(x)及y=x的函数图象
如图所示,由图可得交点有3个.
答案 C例2 (1)已知奇函数f(x)的定义域是{x|x≠0,x∈R},且在(0,+∞)上单调递增,若f(1)=0,则满足x·f(x)<0的x的取值范围是____________.热点二 利用数形结合思想解不等式、求参数范围由图可知x·f(x)<0的x的取值范围是
(-1,0)∪(0,1).解析 作出符合条件的一个函数图象
草图即可,(-1,0)∪(0,1)(2)若不等式|x-2a|≥ x+a-1对x∈R恒成立,则a的取值范围是________.解析 作出y=|x-2a|和y= x+a-1的简图,依题意知应有2a≤2-2a,故a≤ .变式训练2 (1)设A={(x,y)|x2+(y-1)2=1},B={(x,y)|x+y+m≥0},则使A?B成立的实数m的取值范围是_______.解析 集合A是一个圆x2+(y-1)2=1上的点的集合,
集合B是一个不等式x+y+m≥0表示的平面区域内的点的集合,要使A?B,则应使圆被平面区域所包含
(如图),即直线x+y+m=0应与圆相切或相离
(在圆的下方),例3 (1)已知P是直线l:3x+4y+8=0上的动点,PA、PB是圆x2+y2-2x-2y+1=0的两条切线,A、B是切点,C是圆心,则四边形PACB面积的最小值为________.热点三 利用数形结合思想解最值问题解析 从运动的观点看问题,当动点P沿
直线3x+4y+8=0向左上方或右下方无穷
远处运动时,当点P从左上、右下两个方向向中间运动时,S四边形PACB变小,
显然,当点P到达一个最特殊的位置,即CP垂直直线l时,S四边形PACB应有唯一的最小值,解析 画出可行域如图,所求的x2+y2-
6x+9=(x-3)2+y2是点Q(3,0)到可行域上
的点的距离的平方,由图形知最小值为Q到射线x-y-1=0
(x≥0)的距离d的平方,最大值为|QA|2=16.∴取值范围是[2,16].
答案 B变式训练3(1)(2013·重庆)设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
A.6 B.4 C.3 D.2解析 由题意,知圆的圆心坐标为(3,-1),圆的半径长为2,
|PQ|的最小值为圆心到直线x=-3的距离减去圆的半径长,
所以|PQ|min=3-(-3)-2=4.故选B.B又 的几何意义是可行域内的点与坐标原点
连线的斜率k.解析 可行域如图所示.由图知,过点A的直线OA的斜率最小.答案 21.在数学中函数的图象、方程的曲线、不等式所表示的平面区域、向量的几何意义、复数的几何意义等都实现以形助数的途径,当试题中涉及这些问题的数量关系时,我们可以通过图形分析这些数量关系,达到解题的目的.本讲规律总结2.有些图形问题,单纯从图形上无法看出问题的结论,这就要对图形进行数量上的分析,通过数的帮助达到解题的目的.
3.利用数形结合解题,有时只需把图象大致形状画出即可,不需要精确图象.4.数形结合思想常用模型:一次、二次函数图象;斜率公式;两点间的距离公式(或向量的模、复数的模);点到直线的距离公式等.真题感悟押题精练真题与押题12真题感悟34解析 设P(x,0),设C1(2,3)关于x轴的对称点为C1′(2,-3),12真题感悟34答案 A12真题感悟34解析 ∵∠AOB=90°,∴点O在圆C上.
设直线2x+y-4=0与圆C相切于点D,
则点C与点O间的距离等于它到直线2x+y-4=0的距离,
∴点C在以O为焦点,以直线2x+y-4=0为准线的抛物线上,
∴当且仅当O,C,D共线时,圆的直径最小为|OD|.12真题感悟3412真题感悟34答案 A12真题感悟34解析 函数y=|f(x)|的图象如图.
①当a=0时,|f(x)|≥ax显然成立.
②当a>0时,只需在x>0时,
ln(x+1)≥ax成立.
比较对数函数与一次函数y=ax的增长速度.
显然不存在a>0使ln(x+1)≥ax在x>0上恒成立.12真题感悟34③当a<0时,只需在x<0时,x2-2x≥ax成立.
即a≥x-2成立,所以a≥-2.
综上所述:-2≤a≤0.故选D.
答案 D12真题感悟344.(2014·天津)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________.12真题感悟34解析 设y1=f(x)=|x2+3x|,y2=a|x-1|,在同一直角坐标系中作出y1=|x2+3x|,
y2=a|x-1|的图象如图所示.由图可知f(x)-a|x-1|=0有4个互异的实数根等价于y1=|x2+3x|与y2=a|x-1|的图象有4个不同的交点.当4个交点横坐标都小于1时,12真题感悟34消y得x2+(3-a)x+a=0,故Δ=a2-10a+9>0,
且x1+x2=a-3<2,x1x2=a<1,联立可得0
且x3+x4=a-3>2,x3x4=a>1,联立可得a>9,
综上知,0
答案 (0,1)∪(9,+∞)押题精练1231.方程|x2-2x|=a2+1(a>0)的解的个数是( )
A.1 B.2 C.3 D.4456解析 (数形结合法)
∵a>0,∴a2+1>1.∴y=|x2-2x|的图象与y=a2+1的图象总有两个交点.而y=|x2-2x|的图象如图,B2.不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.(-∞,-1]∪[4,+∞)
B.(-∞,-2]∪[5,+∞)
C.[1,2]
D.(-∞,1]∪[2,+∞)押题精练123456押题精练123456画出函数f(x)的图象,如图,可以看出函数f(x)的最大值为4,
故只要a2-3a≥4即可,
解得a≤-1或a≥4.正确选项为A.答案 A3.经过P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的斜率k和倾斜角α的取值范围分别为________,________.押题精练123456解析 如图所示,结合图形:为使l与
线段AB总有公共点,则kPA≤k≤kPB,而kPB>0,kPA<0,押题精练123456故k<0时,倾斜角α为钝角,k=0时,α=0,k>0时,α为锐角.押题精练123456押题精练123456押题精练123456解析 由题意知原点O到直线x+y-2=0的距离为|OM|的最小值.押题精练123456押题精练1234566.设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;押题精练123456解 函数g(x)=bx2-ln x的定义域为(0,+∞),
f′(x)=3ax2-3a?f′(1)=0,g′(x)=2bx- ?g′(1)=2b-1,依题意得2b-1=0,所以b= .押题精练123456押题精练123456即g(x)在(1,+∞)上单调递增,当a=0时,方程F(x)=a2不可能有四个解;
当a<0,x∈(-∞,-1)时,f′(x)<0,
即f(x)在(-∞,-1)上单调递减,x∈(-1,0)时,f′(x)>0,
即f(x)在(-1,0)上单调递增,
所以当x=-1时,f(x)取得极小值f(-1)=2a,押题精练123456又f(0)=0,所以F(x)的图象如图(1)所示,从图象可以看出F(x)=a2不可能有四个解.
当a>0,x∈(-∞,-1)时,f′(x)>0,
即f(x)在(-∞,-1)上单调递增,x∈(-1,0)时,f′(x)<0,
即f(x)在(-1,0)上单调递减,
所以当x=-1时,f(x)取得极大值f(-1)=2a.押题精练123456又f(0)=0,所以F(x)的图象如图(2)所示,
同课章节目录
