苏教版三年级下册数学6.3 面积的计算(课件)(共31张PPT)
文档属性
| 名称 | 苏教版三年级下册数学6.3 面积的计算(课件)(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 11:16:44 | ||
图片预览



文档简介
(共31张PPT)
第六单元 长方形和正方形的面积
面积的计算
苏教版三年级下册
1.经历长方形和正方形面积计算公式的推导过程,理解并掌握这两个面积计算公式,能运用公式进行长方形和正方形的面积计算,并能用来解决简单的实际问题。
2.在学习活动中发展观察能力、操作能力、空间想象能力和抽象概括能力,培养符号感。进一步培养合作意识和合作能力。
我们在前面学习了面积和面积单位的意义。
平方厘米
平方分米
平方米
测量较小物体的面积时常用平方厘米作单位;
测量稍大物体的面积时常用平方分米作单位;
测量较大物体的面积时常用平方米作单位。
如果给你一个长方形或者正方形,怎么求出面积呢?你有什么好方法吗?
课堂导入
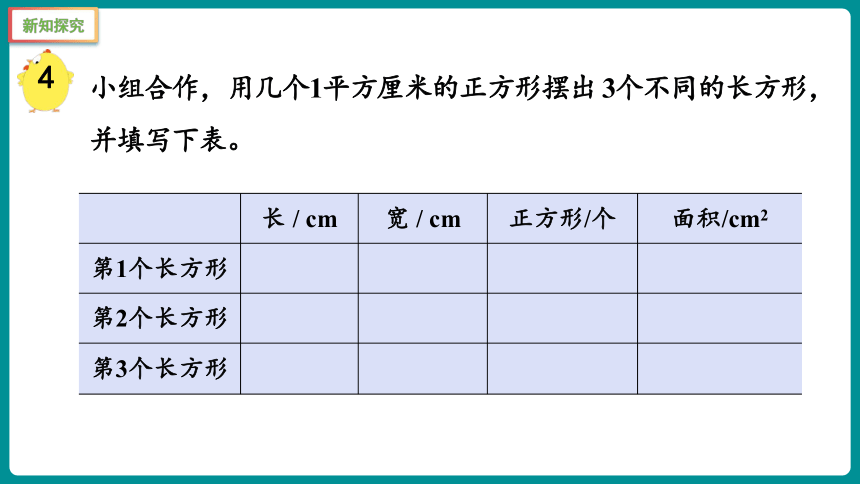
小组合作,用几个1平方厘米的正方形摆出 3个不同的长方形,并填写下表。
4
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
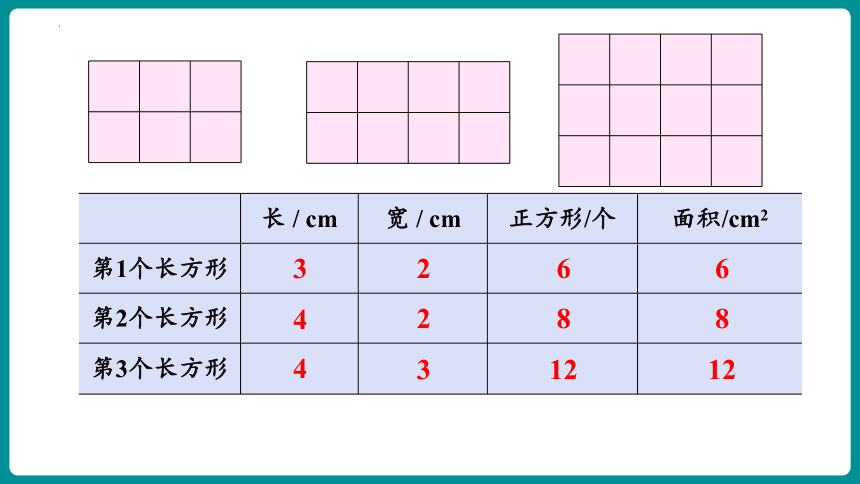
3
2
6
6
4
2
8
8
4
3
12
12
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
3
2
6
6
4
2
8
8
4
3
12
12
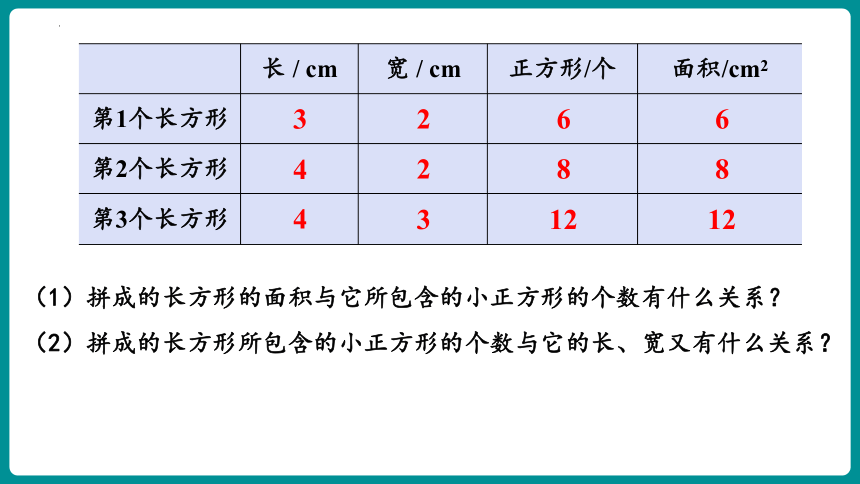
(1)拼成的长方形的面积与它所包含的小正方形的个数有什么关系?
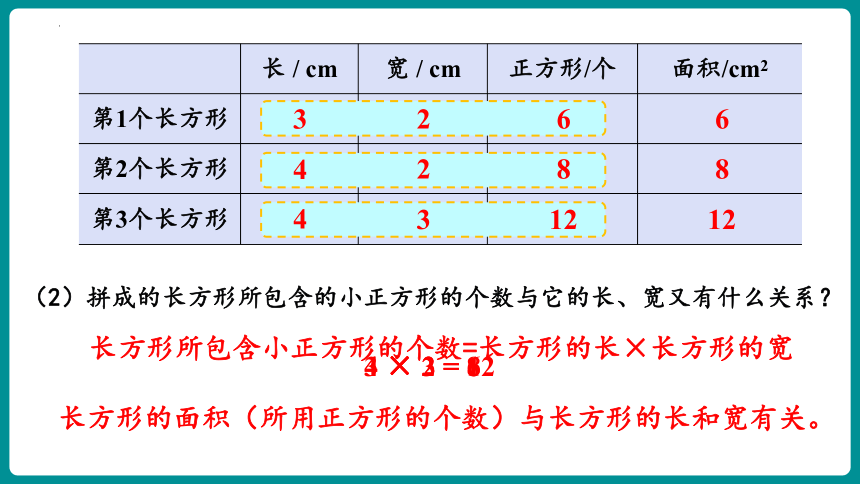
(2)拼成的长方形所包含的小正方形的个数与它的长、宽又有什么关系?
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
3
2
4
2
4
3
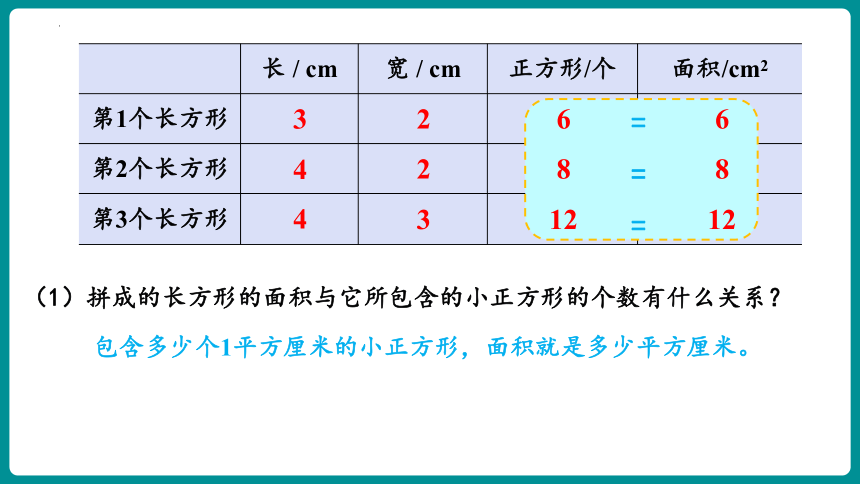
(1)拼成的长方形的面积与它所包含的小正方形的个数有什么关系?
6
6
8
8
12
12
=
=
=
包含多少个1平方厘米的小正方形,面积就是多少平方厘米。
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
6
8
12
(2)拼成的长方形所包含的小正方形的个数与它的长、宽又有什么关系?
3 × 2 = 6
4 × 2 = 8
4 × 3 = 12
3
2
6
4
2
8
4
3
12
长方形所包含小正方形的个数=长方形的长×长方形的宽
长方形的面积(所用正方形的个数)与长方形的长和宽有关。
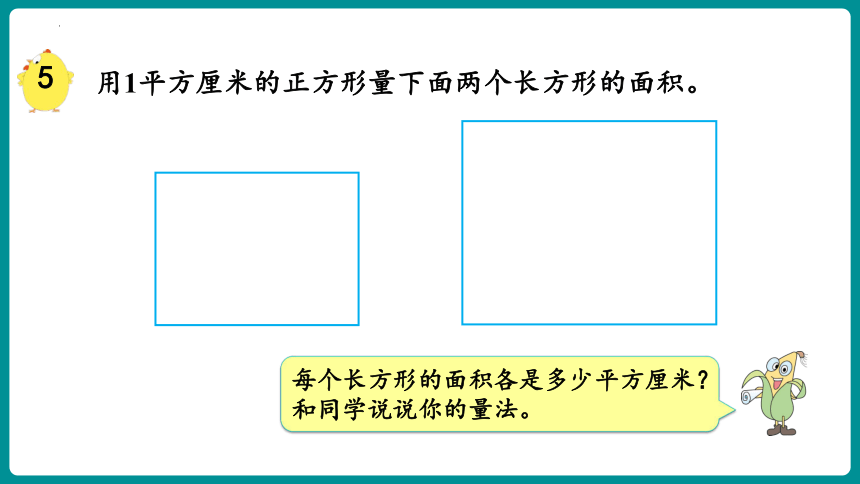
用1平方厘米的正方形量下面两个长方形的面积。
每个长方形的面积各是多少平方厘米? 和同学说说你的量法。
5
1
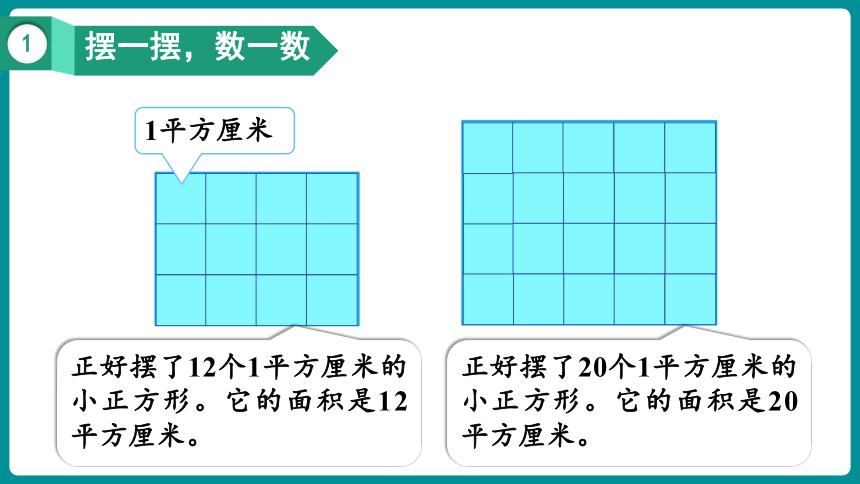
摆一摆,数一数
正好摆了12个1平方厘米的小正方形。它的面积是12平方厘米。
1平方厘米
正好摆了20个1平方厘米的小正方形。它的面积是20平方厘米。
2
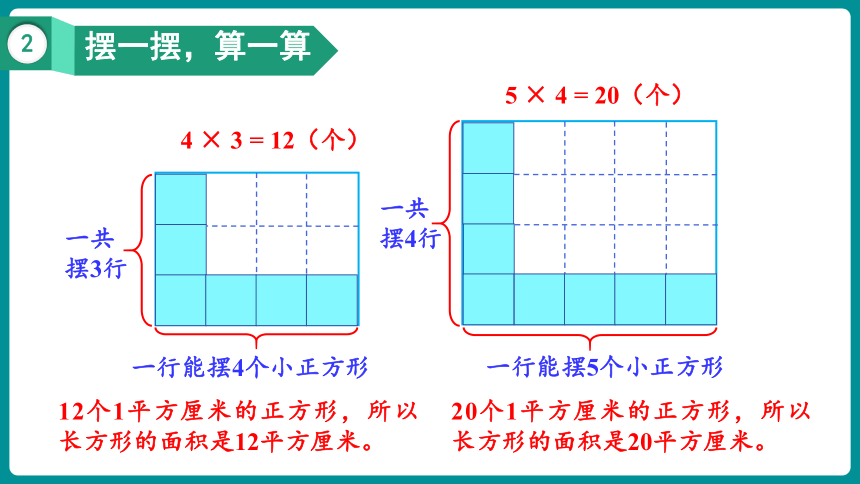
摆一摆,算一算
一行能摆4个小正方形
一共摆3行
4 × 3 = 12(个)
12个1平方厘米的正方形,所以长方形的面积是12平方厘米。
一行能摆5个小正方形
一共摆4行
5 × 4 = 20(个)
20个1平方厘米的正方形,所以长方形的面积是20平方厘米。
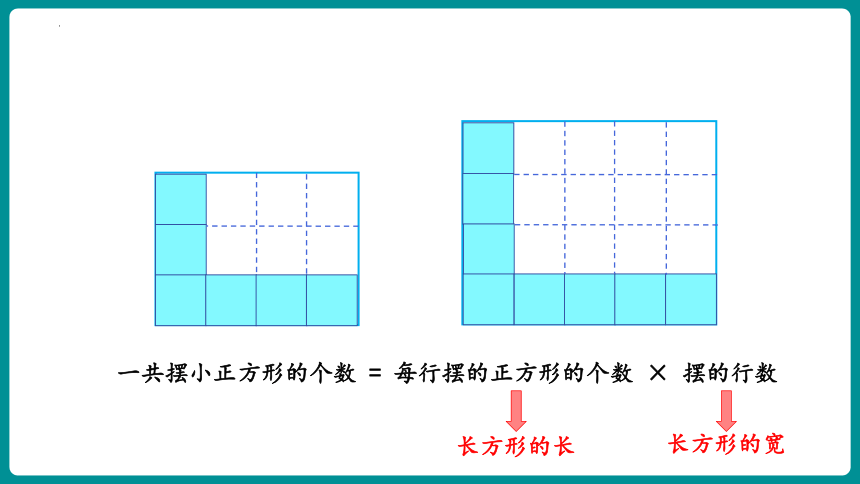
一共摆小正方形的个数 = 每行摆的正方形的个数 × 摆的行数
长方形的长
长方形的宽
思考:为什么要用面积单位把长方形全部铺满?
第二种情况为什么不用铺满?
尽管只铺了一部分,通过想象,也能数出面积单位的个数。
铺满长方形用了几个面积单位,长方形的面积就是多少。
你是怎么知道的?把你的想法和同学交流。
下面长方形的面积是多少平方厘米?
6
7 cm
2 cm
表明在这个长方形一行可以摆7个1平方厘米的小正方形。
表明可以摆2行,每行7个1平方厘米的小正方形。
下面长方形的面积是多少平方厘米?
6
7 cm
2 cm
表明在这个长方形一行可以摆7个1平方厘米的小正方形。
表明可以摆2行,每行7个1平方厘米的小正方形。
小正方形的个数 = 7 × 2 = 14(个)
长方形的面积 = 长7 cm × 宽2 cm = 14平方厘米
…
每行正方形的个数
…
行数
…
…
…
长方形的面积与什么有关? 可以怎样求长方形的面积?
长方形的面积 = 长 × 宽
如果用 S 表示长方形的面积, 用 a 和b 分别表示长方形的长和宽, 上面的公式可以写成:
S = a × b
a
b
正方形有什么特点? 怎样求正方形的面积?
当长方形的长和宽相等时,就会得到特殊的长方形,即正方形,此时长方形的长和宽称为正方形的边长。
正方形的四条边都相等
长方形的面积 = 长 × 宽
正方形的面积 = 长 × 宽
…
…
= 边长 × 边长
…
…
当长方形的长和宽相等时,就会得到特殊的长方形,即正方形,此时长方形的长和宽称为正方形的边长。
正方形的四条边都相等
正方形的面积 = 边长 × 边长
如果用 S 表示正方形的面积, 用 a 表示正方形的边长, 上面的公式可以写成:
a
a
S = a × a
回顾一下, 长方形面积公式是怎样推导出来的? 正方形面积公式呢?
用小正方形摆出不同的长方形,看出面积与长和宽有关。
长方形包含的小正方形的个数,等于长乘宽的积。
根据长方形面积公式推导出正方形面积公式。
计算下面各图形的面积。
9 × 9 = 81(平方米)
6 × 4 = 24(平方分米)
1.一张长方形纸,如下图。
30厘米
21厘米
30×21=630(平方厘米)
答:它的面积是630平方厘米。
长方形的面积=长×宽
(1)它的面积是多少平方厘米?
(2)如果从这张纸上剪下一个最大的正方形,这
个正方形的面积是多少?
30厘米
21厘米
21×21=441(平方厘米)
答:它的面积是441平方厘米。
正方形的边长等于长方形的宽。
正方形的面积=边长×边长
2.一个长方形长3米,宽10分米,这个长方形的面积是多少平方分米?
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
3米=30分米
先统一单位再计算。
3.填空。
(1)王阿姨家的客厅长6( ),宽4( ),
面积是( )。
(2)边长1米的正方形,面积是( )。
(3)一个正方形的边长是11分米,面积是(
),周长是( )。
(4)长方形的面积是128平方米,宽是8米,长
是( )。
米
米
24平方米
1平方米
121
平方分米
44分米
16米
灵活运用周长和面积公式。
A.120米 B.240米 C.320米 D.120平方米
E.360平方米
4.选择。
有一个长方形操场,宽是40米,长是宽的3倍。长是( )。
小红沿这个操场跑一圈,要跑( )。
C
40×3=120(米)
(120+40)×2=320(米)
A
求下面图形的面积。
45+30=75(平方厘米)
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
15-10=5厘米
15×(9-6)=45(平方厘米)
6×(15-10)=30(平方厘米)
方法一
拓展提升
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
45+30=75(平方厘米)
15-10=5厘米
9×(15-10)=45(平方厘米)
10×(9-6)=30(平方厘米)
方法二
求下面图形的面积。
15×9=135(平方厘米)
10×6=60(平方厘米)
135-60=75(平方厘米)
答:图形的面积是75平方厘米。
15厘米
10厘米
6厘米
9厘米
方法三
求下面图形的面积。
解决此类问题,可以先将一个复杂的不规则图形割补成几个简单的规则图形,分别计算出各个规则图形的面积,再求出它们的和或差即可。
解题技巧归纳总结
长方形和正方形面积计算公式
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的长=面积÷宽
长方形的宽=面积÷长
这节课你有什么收获?
第六单元 长方形和正方形的面积
面积的计算
苏教版三年级下册
1.经历长方形和正方形面积计算公式的推导过程,理解并掌握这两个面积计算公式,能运用公式进行长方形和正方形的面积计算,并能用来解决简单的实际问题。
2.在学习活动中发展观察能力、操作能力、空间想象能力和抽象概括能力,培养符号感。进一步培养合作意识和合作能力。
我们在前面学习了面积和面积单位的意义。
平方厘米
平方分米
平方米
测量较小物体的面积时常用平方厘米作单位;
测量稍大物体的面积时常用平方分米作单位;
测量较大物体的面积时常用平方米作单位。
如果给你一个长方形或者正方形,怎么求出面积呢?你有什么好方法吗?
课堂导入
小组合作,用几个1平方厘米的正方形摆出 3个不同的长方形,并填写下表。
4
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
3
2
6
6
4
2
8
8
4
3
12
12
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
3
2
6
6
4
2
8
8
4
3
12
12
(1)拼成的长方形的面积与它所包含的小正方形的个数有什么关系?
(2)拼成的长方形所包含的小正方形的个数与它的长、宽又有什么关系?
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
3
2
4
2
4
3
(1)拼成的长方形的面积与它所包含的小正方形的个数有什么关系?
6
6
8
8
12
12
=
=
=
包含多少个1平方厘米的小正方形,面积就是多少平方厘米。
长 / cm 宽 / cm 正方形/个 面积/cm2
第1个长方形
第2个长方形
第3个长方形
6
8
12
(2)拼成的长方形所包含的小正方形的个数与它的长、宽又有什么关系?
3 × 2 = 6
4 × 2 = 8
4 × 3 = 12
3
2
6
4
2
8
4
3
12
长方形所包含小正方形的个数=长方形的长×长方形的宽
长方形的面积(所用正方形的个数)与长方形的长和宽有关。
用1平方厘米的正方形量下面两个长方形的面积。
每个长方形的面积各是多少平方厘米? 和同学说说你的量法。
5
1
摆一摆,数一数
正好摆了12个1平方厘米的小正方形。它的面积是12平方厘米。
1平方厘米
正好摆了20个1平方厘米的小正方形。它的面积是20平方厘米。
2
摆一摆,算一算
一行能摆4个小正方形
一共摆3行
4 × 3 = 12(个)
12个1平方厘米的正方形,所以长方形的面积是12平方厘米。
一行能摆5个小正方形
一共摆4行
5 × 4 = 20(个)
20个1平方厘米的正方形,所以长方形的面积是20平方厘米。
一共摆小正方形的个数 = 每行摆的正方形的个数 × 摆的行数
长方形的长
长方形的宽
思考:为什么要用面积单位把长方形全部铺满?
第二种情况为什么不用铺满?
尽管只铺了一部分,通过想象,也能数出面积单位的个数。
铺满长方形用了几个面积单位,长方形的面积就是多少。
你是怎么知道的?把你的想法和同学交流。
下面长方形的面积是多少平方厘米?
6
7 cm
2 cm
表明在这个长方形一行可以摆7个1平方厘米的小正方形。
表明可以摆2行,每行7个1平方厘米的小正方形。
下面长方形的面积是多少平方厘米?
6
7 cm
2 cm
表明在这个长方形一行可以摆7个1平方厘米的小正方形。
表明可以摆2行,每行7个1平方厘米的小正方形。
小正方形的个数 = 7 × 2 = 14(个)
长方形的面积 = 长7 cm × 宽2 cm = 14平方厘米
…
每行正方形的个数
…
行数
…
…
…
长方形的面积与什么有关? 可以怎样求长方形的面积?
长方形的面积 = 长 × 宽
如果用 S 表示长方形的面积, 用 a 和b 分别表示长方形的长和宽, 上面的公式可以写成:
S = a × b
a
b
正方形有什么特点? 怎样求正方形的面积?
当长方形的长和宽相等时,就会得到特殊的长方形,即正方形,此时长方形的长和宽称为正方形的边长。
正方形的四条边都相等
长方形的面积 = 长 × 宽
正方形的面积 = 长 × 宽
…
…
= 边长 × 边长
…
…
当长方形的长和宽相等时,就会得到特殊的长方形,即正方形,此时长方形的长和宽称为正方形的边长。
正方形的四条边都相等
正方形的面积 = 边长 × 边长
如果用 S 表示正方形的面积, 用 a 表示正方形的边长, 上面的公式可以写成:
a
a
S = a × a
回顾一下, 长方形面积公式是怎样推导出来的? 正方形面积公式呢?
用小正方形摆出不同的长方形,看出面积与长和宽有关。
长方形包含的小正方形的个数,等于长乘宽的积。
根据长方形面积公式推导出正方形面积公式。
计算下面各图形的面积。
9 × 9 = 81(平方米)
6 × 4 = 24(平方分米)
1.一张长方形纸,如下图。
30厘米
21厘米
30×21=630(平方厘米)
答:它的面积是630平方厘米。
长方形的面积=长×宽
(1)它的面积是多少平方厘米?
(2)如果从这张纸上剪下一个最大的正方形,这
个正方形的面积是多少?
30厘米
21厘米
21×21=441(平方厘米)
答:它的面积是441平方厘米。
正方形的边长等于长方形的宽。
正方形的面积=边长×边长
2.一个长方形长3米,宽10分米,这个长方形的面积是多少平方分米?
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
3米=30分米
先统一单位再计算。
3.填空。
(1)王阿姨家的客厅长6( ),宽4( ),
面积是( )。
(2)边长1米的正方形,面积是( )。
(3)一个正方形的边长是11分米,面积是(
),周长是( )。
(4)长方形的面积是128平方米,宽是8米,长
是( )。
米
米
24平方米
1平方米
121
平方分米
44分米
16米
灵活运用周长和面积公式。
A.120米 B.240米 C.320米 D.120平方米
E.360平方米
4.选择。
有一个长方形操场,宽是40米,长是宽的3倍。长是( )。
小红沿这个操场跑一圈,要跑( )。
C
40×3=120(米)
(120+40)×2=320(米)
A
求下面图形的面积。
45+30=75(平方厘米)
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
15-10=5厘米
15×(9-6)=45(平方厘米)
6×(15-10)=30(平方厘米)
方法一
拓展提升
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
45+30=75(平方厘米)
15-10=5厘米
9×(15-10)=45(平方厘米)
10×(9-6)=30(平方厘米)
方法二
求下面图形的面积。
15×9=135(平方厘米)
10×6=60(平方厘米)
135-60=75(平方厘米)
答:图形的面积是75平方厘米。
15厘米
10厘米
6厘米
9厘米
方法三
求下面图形的面积。
解决此类问题,可以先将一个复杂的不规则图形割补成几个简单的规则图形,分别计算出各个规则图形的面积,再求出它们的和或差即可。
解题技巧归纳总结
长方形和正方形面积计算公式
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的长=面积÷宽
长方形的宽=面积÷长
这节课你有什么收获?
