【高考专辑】【专题4】2015年高三数学(理)【押题精练】三角变换与解三角形
文档属性
| 名称 | 【高考专辑】【专题4】2015年高三数学(理)【押题精练】三角变换与解三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 20:58:39 | ||
图片预览










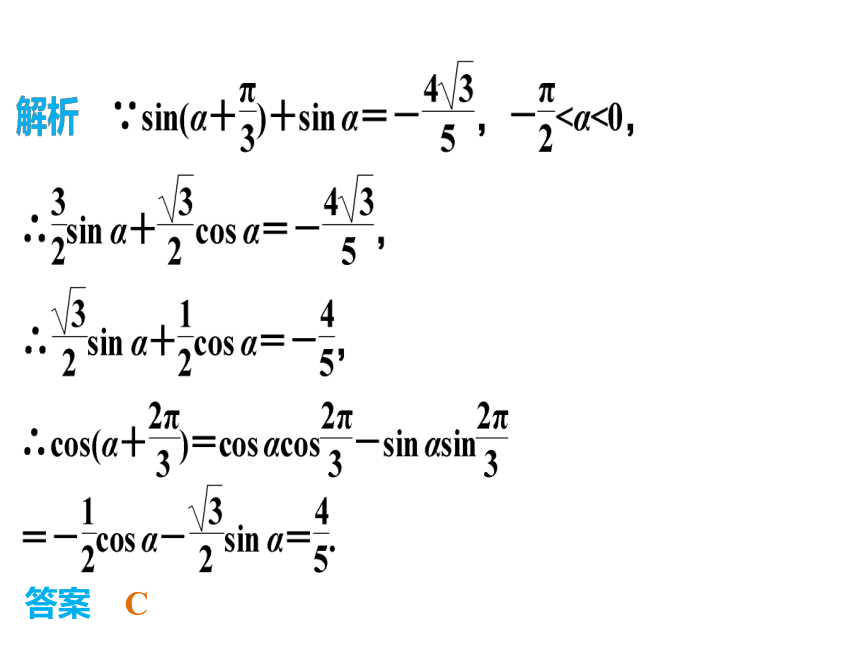
文档简介
课件57张PPT。专题四
三角变换与解三角形三角变换与解三角形主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题1主干知识梳理1.两角和与差的正弦、余弦、正切公式
(1)sin(α±β)=sin αcos β±cos αsin β.
(2)cos(α±β)=cos αcos β?sin αsin β.2.二倍角的正弦、余弦、正切公式
(1)sin 2α=2sin αcos α.
(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.3.三角恒等式的证明方法
(1)从等式的一边推导变形到另一边,一般是化繁为简.
(2)等式的两边同时变形为同一个式子.
(3)将式子变形后再证明.5.余弦定理
a2=b2+c2-2bccos A,b2=a2+c2-2accos B,
c2=a2+b2-2abcos C.变形:b2+c2-a2=2bccos A,a2+c2-b2=2accos B,a2+b2-c2=2abcos C.7.解三角形
(1)已知两角及一边,利用正弦定理求解.
(2)已知两边及一边的对角,利用正弦定理或余弦定理求解,解的情况可能不唯一.
(3)已知两边及其夹角,利用余弦定理求解.
(4)已知三边,利用余弦定理求解.热点一 三角变换热点二 解三角形热点三 正、余弦定理的实际应用热点分类突破热点一 三角变换答案 C思维启迪
先对已知式子进行变形,
得三角函数值的式子,再利用范围探求角的关系.即sin αcos β=cos α+cos αsin β,答案 B变式训练1又θ是第二象限角,热点二 解三角形∴ccos B+2acos C+bcos C=0,
∴sin Ccos B+sin Bcos C+2sin Acos C=0,
∴sin A+2sin Acos C=0,
∵sin A≠0,(2)求△ABC面积的最大值.∴a2+b2+ab=3,∴3ab≤3,即ab≤1.变式训练2 答案 A解析 ∵c2=(a-b)2+6,∴c2=a2+b2-2ab+6.①由①②得ab=6.答案 C例3 (2013·江苏)如图,游客从某旅游景
区的景点A处下山至C处有两种路径.一
种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量cos A= ,cos C= .热点三 正、余弦定理的实际应用(1)求索道AB的长;思维启迪
直接求sin B,利用正弦定理求AB.从而sin B=sin[π-(A+C)]=sin(A+C)
=sin Acos C+cos Asin C所以索道AB的长为1 040 m.(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?思维启迪
利用余弦定理和函数思想,将甲乙距离表示为乙出发后时间t的函数.解 假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.设乙步行的速度为v m/min,变式训练3解 过点A作AD⊥BC,交BC的延长线于点D.
因为∠CAD=45°,AC=10海里,
所以△ACD是等腰直角三角形.在Rt△ABD中,因为∠DAB=60°,因为中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行,1.求解恒等变换问题的基本思路
一角二名三结构,即用化归转化思想“去异求同”的过程,具体分析如下:
(1)首先观察角与角之间的关系,注意角的一些常用变换形式,角的变换是三角函数变换的核心.
(2)其次看函数名称之间的关系,通常“切化弦”.
(3)再次观察代数式的结构特点.本讲规律总结真题感悟押题精练真题与押题12真题感悟12真题感悟用降幂公式化简得:4sin 2α=-3cos 2α,答案 C真题感悟21真题感悟21真题感悟21押题精练12押题精练12押题精练12∵sin C≠0,∴1+cos(A+B)=1,cos(A+B)=0.即△ABC是以角C为直角的直角三角形.押题精练12其值不确定,故③不正确;押题精练12∴cos2A+cos2B=cos2A+sin2A=1=sin2C,
故④正确.
答案 D押题精练122.在△ABC中,角A,B,C所对的边分别为a,b,c,q=(2a,1),p=(2b-c,cos C),且q∥p.
(1)求sin A的值;解 ∵q=(2a,1),p=(2b-c,cos C)且q∥p,
∴2b-c=2acos C,
由正弦定理得2sin Acos C=2sin B-sin C,
又sin B=sin(A+C)=sin Acos C+cos Asin C,押题精练12押题精练12押题精练12
三角变换与解三角形三角变换与解三角形主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题1主干知识梳理1.两角和与差的正弦、余弦、正切公式
(1)sin(α±β)=sin αcos β±cos αsin β.
(2)cos(α±β)=cos αcos β?sin αsin β.2.二倍角的正弦、余弦、正切公式
(1)sin 2α=2sin αcos α.
(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.3.三角恒等式的证明方法
(1)从等式的一边推导变形到另一边,一般是化繁为简.
(2)等式的两边同时变形为同一个式子.
(3)将式子变形后再证明.5.余弦定理
a2=b2+c2-2bccos A,b2=a2+c2-2accos B,
c2=a2+b2-2abcos C.变形:b2+c2-a2=2bccos A,a2+c2-b2=2accos B,a2+b2-c2=2abcos C.7.解三角形
(1)已知两角及一边,利用正弦定理求解.
(2)已知两边及一边的对角,利用正弦定理或余弦定理求解,解的情况可能不唯一.
(3)已知两边及其夹角,利用余弦定理求解.
(4)已知三边,利用余弦定理求解.热点一 三角变换热点二 解三角形热点三 正、余弦定理的实际应用热点分类突破热点一 三角变换答案 C思维启迪
先对已知式子进行变形,
得三角函数值的式子,再利用范围探求角的关系.即sin αcos β=cos α+cos αsin β,答案 B变式训练1又θ是第二象限角,热点二 解三角形∴ccos B+2acos C+bcos C=0,
∴sin Ccos B+sin Bcos C+2sin Acos C=0,
∴sin A+2sin Acos C=0,
∵sin A≠0,(2)求△ABC面积的最大值.∴a2+b2+ab=3,∴3ab≤3,即ab≤1.变式训练2 答案 A解析 ∵c2=(a-b)2+6,∴c2=a2+b2-2ab+6.①由①②得ab=6.答案 C例3 (2013·江苏)如图,游客从某旅游景
区的景点A处下山至C处有两种路径.一
种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量cos A= ,cos C= .热点三 正、余弦定理的实际应用(1)求索道AB的长;思维启迪
直接求sin B,利用正弦定理求AB.从而sin B=sin[π-(A+C)]=sin(A+C)
=sin Acos C+cos Asin C所以索道AB的长为1 040 m.(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?思维启迪
利用余弦定理和函数思想,将甲乙距离表示为乙出发后时间t的函数.解 假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.设乙步行的速度为v m/min,变式训练3解 过点A作AD⊥BC,交BC的延长线于点D.
因为∠CAD=45°,AC=10海里,
所以△ACD是等腰直角三角形.在Rt△ABD中,因为∠DAB=60°,因为中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行,1.求解恒等变换问题的基本思路
一角二名三结构,即用化归转化思想“去异求同”的过程,具体分析如下:
(1)首先观察角与角之间的关系,注意角的一些常用变换形式,角的变换是三角函数变换的核心.
(2)其次看函数名称之间的关系,通常“切化弦”.
(3)再次观察代数式的结构特点.本讲规律总结真题感悟押题精练真题与押题12真题感悟12真题感悟用降幂公式化简得:4sin 2α=-3cos 2α,答案 C真题感悟21真题感悟21真题感悟21押题精练12押题精练12押题精练12∵sin C≠0,∴1+cos(A+B)=1,cos(A+B)=0.即△ABC是以角C为直角的直角三角形.押题精练12其值不确定,故③不正确;押题精练12∴cos2A+cos2B=cos2A+sin2A=1=sin2C,
故④正确.
答案 D押题精练122.在△ABC中,角A,B,C所对的边分别为a,b,c,q=(2a,1),p=(2b-c,cos C),且q∥p.
(1)求sin A的值;解 ∵q=(2a,1),p=(2b-c,cos C)且q∥p,
∴2b-c=2acos C,
由正弦定理得2sin Acos C=2sin B-sin C,
又sin B=sin(A+C)=sin Acos C+cos Asin C,押题精练12押题精练12押题精练12
同课章节目录
