苏教版六年级上册数学2、《分数乘法》课件(26张ppt)
文档属性
| 名称 | 苏教版六年级上册数学2、《分数乘法》课件(26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 632.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 11:45:57 | ||
图片预览







文档简介
(共26张PPT)
第二单元
分 数 乘 法
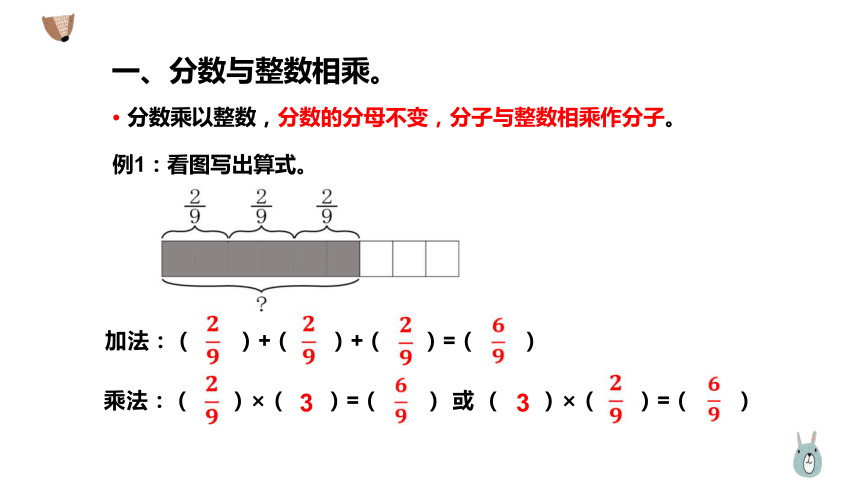
一、分数与整数相乘。
· 分数乘以整数,分数的分母不变,分子与整数相乘作分子。
例1:看图写出算式。
加法:( )+( )+( )=( )
乘法:( )×( )=( ) 或 ( )×( )=( )
3
3
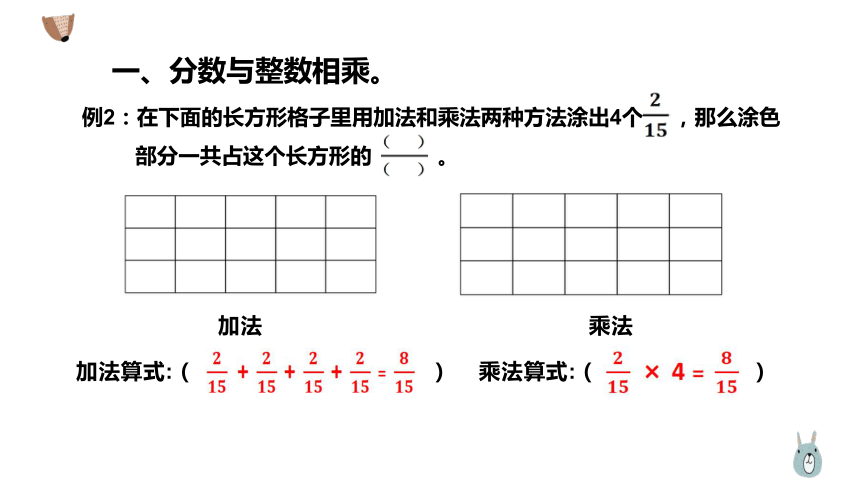
一、分数与整数相乘。
例2:在下面的长方形格子里用加法和乘法两种方法涂出4个 ,那么涂色
部分一共占这个长方形的 。
加法
乘法
加法算式:( ) 乘法算式:( )
例题演练:
1、在( )里填上合适的数。
2、一堆大米, 每天吃 , 5天吃了这堆大米的( ),若每天吃 吨,
则5天吃( )。
3、有一种节能灯平均每天可以节约用电 千瓦·时,那么一个星期可以节
约用电( )千瓦·时
例题演练:
4、认真计算。
5、一根长方体木料长5米,横截面是一个面积为 平方米的正方形,
这根木料的体积是多少立方米?如果沿着长截成3段,那么表面积
增加多少平方米?
例题演练:
6、有两桶油,如果从第一桶中倒出 千克给第二桶,那么这两桶
油的质量正好相等,原来第一桶油比第二桶油重( )千克。
7、一根长方体木料,横截面是面积为 平方米的正方形,把它平行与
横截面截成3段,表面积增加了多少平分米?
8、将一根绳子对折3次,测得每段长度是 米,那么这根绳子的长度
是多少米?
二、求一个数的几分之几是多少的实际问题。
· 求一个数的几分之几是多少,就是用这个数乘以几分之几 。
例1、求9的 是多少 ?
解析:求一个数的几分之几是多少,就是用这个数乘以几分之几,所以求9的 是多少?直接用9乘以 , 9× = 3,所以9的 是 3 。
例2、根据条件把数量关系式补充完整。
(1)五1班的同学近视人数占全班人数的 。
( )× = ( )
全班人数
近视人数
二、求一个数的几分之几是多少的实际问题。
(2)一袋大米,吃掉 。
( )× = ( )
一袋大米
吃掉的大米
例3、某小学为全体师生购入了320本经典读物,其中《趣味数学》类
占 ,那么《趣味数学》读物购买了多少本?
二、求一个数的几分之几是多少的实际问题。
例4、为了不影响学生的健康,学生的书包重量应不超过儿童体重的 ,
小明的体重是35千克,而小明的书包重量是6千克,那么小明的书
包超重了吗?
例5、六(1)班的总人数不少于40人且不多于50人,男生人数占总人数
的 ,则六(1)班男生最多有( )人。
三、一个数比另一个数多(少)几分之几, 求两数相差多少。
· 找单位1的方法:在“占”、“比”、“是”、“相当于”后面的量是单位“1”,
当遇到隐藏单位1时要会将题目补充完整再找单位“1”。
·已知一个数比另一个数多(少)几分之几,求这个数比另一个数多(少)几,
就是变相的求一个数的几分之几是多少。
例1、根据条件画一画、填一填。
三、一个数比另一个数多(少)几分之几, 求两数相差多少。
例1、根据条件画一画、填一填。
例2、在下面题目中的单位“1”下面画线,并把数量关系补充完整。
练习讲解
1、 看图列式计算。
练习讲解
2、小华有63枚邮票,如果他拿出自己邮票枚数的 送给小明,那么两
个人的邮票枚数就一样多。原来小华比小明多( )枚邮票。
3、盱眙小学九月份用电4500千瓦·时,十月份比九月份节约了 ,如果节约1千瓦·时电就能节省0.52元,那么十月份比九月份节约了多少元?
练习讲解
4、甲、乙两瓶里各有水500mL,第一次把甲瓶里的 倒入乙瓶,第二次再把乙瓶里的 倒入甲瓶,第三次把甲瓶里的 倒入乙瓶···就这样来回倒了100次。这时甲瓶里有水( )mL。
5、有三堆棋子,每堆80枚,第一堆中的黑子和第二堆中的白子一样多,第三堆中的 是白子。一共有( )枚白子。
四、分数与分数相乘。
(1)、分数乘以分数,可以理解成求一个分数的几分之几是多少。
例1:看图填空并列式计算。
(2)、分数与分数相乘,就是将分数的分子与分子相乘作为分子,分母
与分母相乘作为分母。最后的结果要是化简后的最简结果。
解析:涂色部分占整个长方形的 ,画斜线部分占涂色部分的 。画斜线部分占整个长方形的几分之几?列式为:
×
四、分数与分数相乘。
例2:看图填空并列式计算。
解析:先把 公顷看成单位“1”,再算出要求的部分占单位“1”的几分之几,
求单位“1”的几分之几就是用单位“1”乘以几分之几。
×
例题演练:
1、计算题。
2、回收1吨废纸可以生产出 吨再生纸,照这样计算,回收 吨废
纸可以生产出再生纸多少吨?
例题演练:
3、学校买来 吨大米,第一周吃了全部的 ,第二周吃了 吨。两周一共吃了多少吨?
4、一批零件平均分给师徒两人加工,师傅完成了自己任务的 ,徒弟完成了自己任务的 。师徒两人一共完成了这批零件的几分之几?
拓展提优:
a×(大于1的数)>a; a×(小于1的数)<a; a×1= a。
例:在○里填“>”“<”或“=”。
五、分数连乘。
(1) ·分数连乘,注意在运算过程中将分子和分母约去公因数,最后的结果
一定要是最简结果。
注意:在计算过程中我们可以将分子和分母进行多次约分。
例题演练:
1、计算题。
2、水果店运来450千克苹果,第一天卖出 ,第二天比第一天多卖出 ,
两天一共卖出( )千克苹果。
例题演练:
3、有一个大西瓜,爸爸吃了 ,剩下的西瓜妈妈吃了一半,另一半
被小乐和小明平均分着吃了,小乐吃了整个西瓜的几分之几 ?
4、如图,三角形ABC的面积是1600平方厘米,已知
三角形ADC的面积是三角形的 ,且AF=FE=ED。
三角形ACF的面积是( )平方厘米。
五、认识倒数。
(1) 如果两个数相乘的积为1,那么这两个数互为倒数;
如果两个数互为倒数,那么这两个数的乘积为1。
例:如果a与b互为倒数,则ab=1;如果ab=1,则a与b互为倒数。
(2) 整数的倒数就是整数分之一;
例:5的倒数是 ,20的倒数是 。 的倒数是50。
(3) 分数的倒数就是将这个分数的分子与分母交换个位置;
例: 的倒数是 ;
五、认识倒数。
(4) ·求小数的倒数时,要先将小数化成分数,再求它的倒数。
例:0.3( )的倒数是 。
例题讲解:
例1:写出下列数的倒数。
解析、分数的倒数就是将这个分数的分子与分母交换个位置;
这边要注意的是不能写成 求小数的倒数时先将小数化成分数再求它的倒数,所以 的倒数是 而 的倒数不能写成 ,要写成 5。
例题演练:
2、1.25的倒数是( ), 与( )互为倒数。 的倒数是( )。
1、在( )里填上合适的数。
3、( )的倒数是它本身,( )没有倒数,最小的质数的倒数是( ),
( )的倒数是最小的合数。
4、已知a与b互为倒数,则 × =( )。
例题演练:
5、
6、如果a和b互为倒数,那么a+b( )a×b。
A、 是倒数 B、 是倒数 C、 和 都是倒数 D、 和 互为倒数
A、大于 B、等于 C、小于 D、无法判断
7、若甲数的倒数大于乙数的倒数,则甲数和乙数相比( )。
A、甲数大 B、乙数大 C、一样大 D、无法确定
8、已知a× =b× = c× =d,并且a,b,c,d都不等于0.把这四个
数按照从小到大的顺序排列。
第二单元
分 数 乘 法
一、分数与整数相乘。
· 分数乘以整数,分数的分母不变,分子与整数相乘作分子。
例1:看图写出算式。
加法:( )+( )+( )=( )
乘法:( )×( )=( ) 或 ( )×( )=( )
3
3
一、分数与整数相乘。
例2:在下面的长方形格子里用加法和乘法两种方法涂出4个 ,那么涂色
部分一共占这个长方形的 。
加法
乘法
加法算式:( ) 乘法算式:( )
例题演练:
1、在( )里填上合适的数。
2、一堆大米, 每天吃 , 5天吃了这堆大米的( ),若每天吃 吨,
则5天吃( )。
3、有一种节能灯平均每天可以节约用电 千瓦·时,那么一个星期可以节
约用电( )千瓦·时
例题演练:
4、认真计算。
5、一根长方体木料长5米,横截面是一个面积为 平方米的正方形,
这根木料的体积是多少立方米?如果沿着长截成3段,那么表面积
增加多少平方米?
例题演练:
6、有两桶油,如果从第一桶中倒出 千克给第二桶,那么这两桶
油的质量正好相等,原来第一桶油比第二桶油重( )千克。
7、一根长方体木料,横截面是面积为 平方米的正方形,把它平行与
横截面截成3段,表面积增加了多少平分米?
8、将一根绳子对折3次,测得每段长度是 米,那么这根绳子的长度
是多少米?
二、求一个数的几分之几是多少的实际问题。
· 求一个数的几分之几是多少,就是用这个数乘以几分之几 。
例1、求9的 是多少 ?
解析:求一个数的几分之几是多少,就是用这个数乘以几分之几,所以求9的 是多少?直接用9乘以 , 9× = 3,所以9的 是 3 。
例2、根据条件把数量关系式补充完整。
(1)五1班的同学近视人数占全班人数的 。
( )× = ( )
全班人数
近视人数
二、求一个数的几分之几是多少的实际问题。
(2)一袋大米,吃掉 。
( )× = ( )
一袋大米
吃掉的大米
例3、某小学为全体师生购入了320本经典读物,其中《趣味数学》类
占 ,那么《趣味数学》读物购买了多少本?
二、求一个数的几分之几是多少的实际问题。
例4、为了不影响学生的健康,学生的书包重量应不超过儿童体重的 ,
小明的体重是35千克,而小明的书包重量是6千克,那么小明的书
包超重了吗?
例5、六(1)班的总人数不少于40人且不多于50人,男生人数占总人数
的 ,则六(1)班男生最多有( )人。
三、一个数比另一个数多(少)几分之几, 求两数相差多少。
· 找单位1的方法:在“占”、“比”、“是”、“相当于”后面的量是单位“1”,
当遇到隐藏单位1时要会将题目补充完整再找单位“1”。
·已知一个数比另一个数多(少)几分之几,求这个数比另一个数多(少)几,
就是变相的求一个数的几分之几是多少。
例1、根据条件画一画、填一填。
三、一个数比另一个数多(少)几分之几, 求两数相差多少。
例1、根据条件画一画、填一填。
例2、在下面题目中的单位“1”下面画线,并把数量关系补充完整。
练习讲解
1、 看图列式计算。
练习讲解
2、小华有63枚邮票,如果他拿出自己邮票枚数的 送给小明,那么两
个人的邮票枚数就一样多。原来小华比小明多( )枚邮票。
3、盱眙小学九月份用电4500千瓦·时,十月份比九月份节约了 ,如果节约1千瓦·时电就能节省0.52元,那么十月份比九月份节约了多少元?
练习讲解
4、甲、乙两瓶里各有水500mL,第一次把甲瓶里的 倒入乙瓶,第二次再把乙瓶里的 倒入甲瓶,第三次把甲瓶里的 倒入乙瓶···就这样来回倒了100次。这时甲瓶里有水( )mL。
5、有三堆棋子,每堆80枚,第一堆中的黑子和第二堆中的白子一样多,第三堆中的 是白子。一共有( )枚白子。
四、分数与分数相乘。
(1)、分数乘以分数,可以理解成求一个分数的几分之几是多少。
例1:看图填空并列式计算。
(2)、分数与分数相乘,就是将分数的分子与分子相乘作为分子,分母
与分母相乘作为分母。最后的结果要是化简后的最简结果。
解析:涂色部分占整个长方形的 ,画斜线部分占涂色部分的 。画斜线部分占整个长方形的几分之几?列式为:
×
四、分数与分数相乘。
例2:看图填空并列式计算。
解析:先把 公顷看成单位“1”,再算出要求的部分占单位“1”的几分之几,
求单位“1”的几分之几就是用单位“1”乘以几分之几。
×
例题演练:
1、计算题。
2、回收1吨废纸可以生产出 吨再生纸,照这样计算,回收 吨废
纸可以生产出再生纸多少吨?
例题演练:
3、学校买来 吨大米,第一周吃了全部的 ,第二周吃了 吨。两周一共吃了多少吨?
4、一批零件平均分给师徒两人加工,师傅完成了自己任务的 ,徒弟完成了自己任务的 。师徒两人一共完成了这批零件的几分之几?
拓展提优:
a×(大于1的数)>a; a×(小于1的数)<a; a×1= a。
例:在○里填“>”“<”或“=”。
五、分数连乘。
(1) ·分数连乘,注意在运算过程中将分子和分母约去公因数,最后的结果
一定要是最简结果。
注意:在计算过程中我们可以将分子和分母进行多次约分。
例题演练:
1、计算题。
2、水果店运来450千克苹果,第一天卖出 ,第二天比第一天多卖出 ,
两天一共卖出( )千克苹果。
例题演练:
3、有一个大西瓜,爸爸吃了 ,剩下的西瓜妈妈吃了一半,另一半
被小乐和小明平均分着吃了,小乐吃了整个西瓜的几分之几 ?
4、如图,三角形ABC的面积是1600平方厘米,已知
三角形ADC的面积是三角形的 ,且AF=FE=ED。
三角形ACF的面积是( )平方厘米。
五、认识倒数。
(1) 如果两个数相乘的积为1,那么这两个数互为倒数;
如果两个数互为倒数,那么这两个数的乘积为1。
例:如果a与b互为倒数,则ab=1;如果ab=1,则a与b互为倒数。
(2) 整数的倒数就是整数分之一;
例:5的倒数是 ,20的倒数是 。 的倒数是50。
(3) 分数的倒数就是将这个分数的分子与分母交换个位置;
例: 的倒数是 ;
五、认识倒数。
(4) ·求小数的倒数时,要先将小数化成分数,再求它的倒数。
例:0.3( )的倒数是 。
例题讲解:
例1:写出下列数的倒数。
解析、分数的倒数就是将这个分数的分子与分母交换个位置;
这边要注意的是不能写成 求小数的倒数时先将小数化成分数再求它的倒数,所以 的倒数是 而 的倒数不能写成 ,要写成 5。
例题演练:
2、1.25的倒数是( ), 与( )互为倒数。 的倒数是( )。
1、在( )里填上合适的数。
3、( )的倒数是它本身,( )没有倒数,最小的质数的倒数是( ),
( )的倒数是最小的合数。
4、已知a与b互为倒数,则 × =( )。
例题演练:
5、
6、如果a和b互为倒数,那么a+b( )a×b。
A、 是倒数 B、 是倒数 C、 和 都是倒数 D、 和 互为倒数
A、大于 B、等于 C、小于 D、无法判断
7、若甲数的倒数大于乙数的倒数,则甲数和乙数相比( )。
A、甲数大 B、乙数大 C、一样大 D、无法确定
8、已知a× =b× = c× =d,并且a,b,c,d都不等于0.把这四个
数按照从小到大的顺序排列。
