3.4.1 分配、和差、比例问题 课件 2023-2024学年湘教版七年级数学上册(17张PPT)
文档属性
| 名称 | 3.4.1 分配、和差、比例问题 课件 2023-2024学年湘教版七年级数学上册(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 18:09:30 | ||
图片预览






文档简介
(共17张PPT)
第三章 一元一次方程
3.4.1 分配、和差、比例问题
1.利用一元一次方程解决和、差、倍、分问题.
2.学会分析复杂问题中的数量关系和等量关系,列出一元一次方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
列等式表示:
y的三分之一等于9 : ____________________________________
x的2倍与10的差等于28 : ________________________________
x的四分之一减2的差等于6 : _____________________________
比a的三倍大5的数等于a的一半:___________________________
2x-10=28
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 配套问题
活动1.某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
讨论:
①本题需要我们解决的问题是什么?
②题目中哪些信息能解决人员安排的问题?
③螺母和螺钉的数量关系如何?
如果设x名
工人生产螺母,怎样列方程?
合作探究
当堂检测
学习目标
课堂总结
自主学习
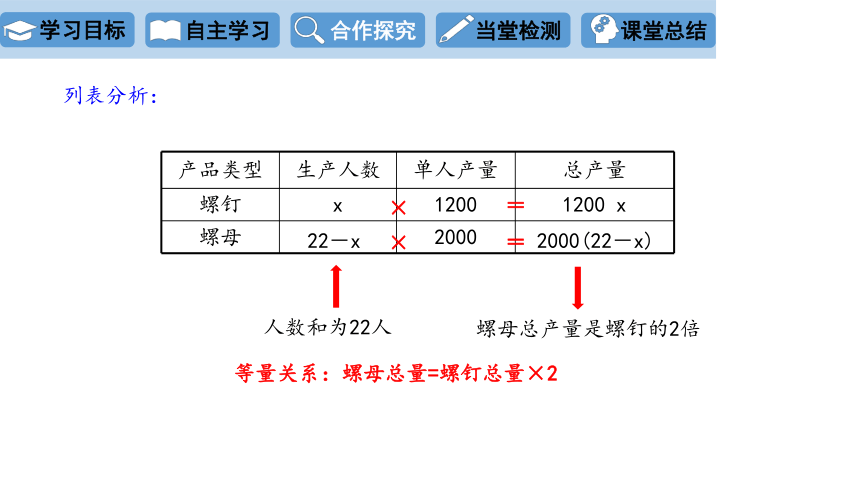
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1200
螺母 2000
×
=
1200 x
人数和为22人
22-x
螺母总产量是螺钉的2倍
×
=
2000(22-x)
等量关系:螺母总量=螺钉总量×2
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设应安排 x 名工人生产螺钉,(22-x)名工人生产螺母.
依题意,得 2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
还有别的方法吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法归纳
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.一套仪器由一个 A 部件和三个 B 部件构成. 用1 立方米钢材可做 40 个 A 部件或 240 个 B 部件.现要用 6 立方米钢材制作这种仪器,应用多少钢材做 A 部件,多少钢材做B部件,才能恰好配成这种仪器?共配成多少套?
分析:由题意知 B 部件的数量是 A 部件数量的 3 倍,可根据这一等量关系式得到方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设应用 x 立方米钢材做 A 部件,
则应用(6-x)立方米做 B 部件.
根据题意,列方程:3×40x = (6-x)×240.
解得 x = 4.
则 6-x = 2.
共配成仪器:4×40=160 (套).
答:应用 4 立方米钢材做 A 部件,2 立方米钢材做 B 部件,共配成仪器160套.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 比例问题
活动2.三个作业队共同使用水泵排涝,如果三个作业队排涝的土地面积之比为4:5:6,而这一次装运水泵和耗用的电力费用共计120元,三个作业队按土地面积比各应负担多少元?
怎么设未知数呢?
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设每份土地排涝分担费用为x元,
那么三个作业队应负担费用分别为4x元,5x元,6x元.
依据题意,得 4x+5x+6x=120.
解方程,得 x=8.
4x=32,5x=40,6x=48.
答:三个作业队各应负担32元、40元、48元.
注意:本题中“设每份土地排涝分担费用x元”属间接设未知数法.当不能或难以直接设未知数时,常用这种方法.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
比例问题:就是把一个数按照一定的比分成若干份.一般需间接设元,设每一份为x,再根据各部分之和等于总体列出方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.质量为45克的某种三色冰淇淋中,咖啡色、红色和白色配料的比为1:2:6,这种三色冰淇淋中,咖啡色、红色和白色配料分别是多少
解:设咖啡色配料为x克,那么红色配料为2x克,白色配料为6x克.
依据题意,得 x+2x+6x=45.
解方程,得 x=5.
2x=10,6x=30.
答:咖啡色、红色和白色配料分别为5克、10克、30克.
合作探究
当堂检测
学习目标
课堂总结
自主学习
小组讨论:运用一元一次方程模型解决实际问题的步骤有哪些?
实际问题
建立方程模型
解方程
检验解的
合理性
分析等量关系
设未知数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.父子两人今年年龄之和为40岁,已知两年前父亲年龄是儿子年龄的8倍,请问两年前父子各几岁?
两年前 今年
儿子
父亲
总计 40
x
8x
x+2
8x+2
解:设两年前儿子为x岁.
依据题意,得
(8x+2)+(x+2)=40.
解方程,得:
x=4. 8x=32.
答:两年前父亲32岁,儿子4岁.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.我国四大发明之一的黑火药是用硝酸钠、硫磺、木炭三种,原料按15:2:3的比例配制而成,现要配制这种火药150公斤,则这三种原料各需要多少公斤?
解:设需要硝酸钠15x公斤,硫磺2x公斤,木炭3x公斤.
依题意得:15x+2x+3x=150
解方程得: x=7.5
15x=15×7.5=112.5 2x=2×7.5=15
3x=3×7.5=22.5
答:硝酸钠需要112.5公斤,硫磺需要15公斤,木炭需要 22.5公斤.
合作探究
当堂检测
学习目标
课堂总结
自主学习
一元一次方程的应用
比例问题
和、差、倍、分问题
步骤
方法:采用间接设元法,通常设每一份为x.
1.设未知数;2.找等量关系;3.列方程;4.解方程;5.检验作答
方法:设其中一个未知量为x,用含x的代数式表示另一个未知量
第三章 一元一次方程
3.4.1 分配、和差、比例问题
1.利用一元一次方程解决和、差、倍、分问题.
2.学会分析复杂问题中的数量关系和等量关系,列出一元一次方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
列等式表示:
y的三分之一等于9 : ____________________________________
x的2倍与10的差等于28 : ________________________________
x的四分之一减2的差等于6 : _____________________________
比a的三倍大5的数等于a的一半:___________________________
2x-10=28
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 配套问题
活动1.某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
讨论:
①本题需要我们解决的问题是什么?
②题目中哪些信息能解决人员安排的问题?
③螺母和螺钉的数量关系如何?
如果设x名
工人生产螺母,怎样列方程?
合作探究
当堂检测
学习目标
课堂总结
自主学习
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1200
螺母 2000
×
=
1200 x
人数和为22人
22-x
螺母总产量是螺钉的2倍
×
=
2000(22-x)
等量关系:螺母总量=螺钉总量×2
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设应安排 x 名工人生产螺钉,(22-x)名工人生产螺母.
依题意,得 2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
还有别的方法吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法归纳
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.一套仪器由一个 A 部件和三个 B 部件构成. 用1 立方米钢材可做 40 个 A 部件或 240 个 B 部件.现要用 6 立方米钢材制作这种仪器,应用多少钢材做 A 部件,多少钢材做B部件,才能恰好配成这种仪器?共配成多少套?
分析:由题意知 B 部件的数量是 A 部件数量的 3 倍,可根据这一等量关系式得到方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设应用 x 立方米钢材做 A 部件,
则应用(6-x)立方米做 B 部件.
根据题意,列方程:3×40x = (6-x)×240.
解得 x = 4.
则 6-x = 2.
共配成仪器:4×40=160 (套).
答:应用 4 立方米钢材做 A 部件,2 立方米钢材做 B 部件,共配成仪器160套.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 比例问题
活动2.三个作业队共同使用水泵排涝,如果三个作业队排涝的土地面积之比为4:5:6,而这一次装运水泵和耗用的电力费用共计120元,三个作业队按土地面积比各应负担多少元?
怎么设未知数呢?
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设每份土地排涝分担费用为x元,
那么三个作业队应负担费用分别为4x元,5x元,6x元.
依据题意,得 4x+5x+6x=120.
解方程,得 x=8.
4x=32,5x=40,6x=48.
答:三个作业队各应负担32元、40元、48元.
注意:本题中“设每份土地排涝分担费用x元”属间接设未知数法.当不能或难以直接设未知数时,常用这种方法.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
比例问题:就是把一个数按照一定的比分成若干份.一般需间接设元,设每一份为x,再根据各部分之和等于总体列出方程.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.质量为45克的某种三色冰淇淋中,咖啡色、红色和白色配料的比为1:2:6,这种三色冰淇淋中,咖啡色、红色和白色配料分别是多少
解:设咖啡色配料为x克,那么红色配料为2x克,白色配料为6x克.
依据题意,得 x+2x+6x=45.
解方程,得 x=5.
2x=10,6x=30.
答:咖啡色、红色和白色配料分别为5克、10克、30克.
合作探究
当堂检测
学习目标
课堂总结
自主学习
小组讨论:运用一元一次方程模型解决实际问题的步骤有哪些?
实际问题
建立方程模型
解方程
检验解的
合理性
分析等量关系
设未知数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.父子两人今年年龄之和为40岁,已知两年前父亲年龄是儿子年龄的8倍,请问两年前父子各几岁?
两年前 今年
儿子
父亲
总计 40
x
8x
x+2
8x+2
解:设两年前儿子为x岁.
依据题意,得
(8x+2)+(x+2)=40.
解方程,得:
x=4. 8x=32.
答:两年前父亲32岁,儿子4岁.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.我国四大发明之一的黑火药是用硝酸钠、硫磺、木炭三种,原料按15:2:3的比例配制而成,现要配制这种火药150公斤,则这三种原料各需要多少公斤?
解:设需要硝酸钠15x公斤,硫磺2x公斤,木炭3x公斤.
依题意得:15x+2x+3x=150
解方程得: x=7.5
15x=15×7.5=112.5 2x=2×7.5=15
3x=3×7.5=22.5
答:硝酸钠需要112.5公斤,硫磺需要15公斤,木炭需要 22.5公斤.
合作探究
当堂检测
学习目标
课堂总结
自主学习
一元一次方程的应用
比例问题
和、差、倍、分问题
步骤
方法:采用间接设元法,通常设每一份为x.
1.设未知数;2.找等量关系;3.列方程;4.解方程;5.检验作答
方法:设其中一个未知量为x,用含x的代数式表示另一个未知量
同课章节目录
