4.3.2 角的度量与计算 课件(共17张PPT) 2023—-2024学年湘教版数学七年级上册
文档属性
| 名称 | 4.3.2 角的度量与计算 课件(共17张PPT) 2023—-2024学年湘教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第四章 图形的认识
4.3.2 角的度量与计算
1.认识角的度量单位度、分、秒,会进行简单的换算.
2.了解余角、补角的概念,掌握余角和补角的性质.
3.会进行角的和、差计算,并能利用余角、补角的知识解决相关问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点一 角的度量单位
1. 叫做直角;
叫做锐角;
叫做钝角.
2.角的度量单位有 、 、 .进制是 .
3. 1°= ′,1′= ″,1°= ″,
1″= ′,1′= °,1周角= °,1平角= °.
平角的一半(即90°的角)
小于直角(即小于90°)的角
大于直角但小于平角(即大于90°但小于180°)的角
度
分
秒
60
60
60
3600
360
180
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点二 余角和补角的定义和性质
1.互为余角和互为补角的概念:
两角之和等于 度,这样的两个角互为余角.
两角之和等于 度,这样的两个角互为补角.
(1)若∠1和∠2互补,则∠1+∠2= ;
(2)若∠3和∠4互余,则∠3+∠4= .
90
180
180°
90°
3
4
1
2
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点二 余角和补角的定义和性质
2.互为余角及互为补角的性质:
同角或等角的余角 ;同角或等角的补角 .
应用举例:∵∠1=∠2,∠1+∠3=90°,∠2+∠4=90°(已知),
∴∠3=∠4(等角的余角相等)
填理由:∵∠1+∠2=180°,∠1+∠3=180°( )
∴∠3=∠4( )
相等
相等
已知
同角的补角相等
探究一 角的单位换算与计算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1.将下列角度进行换算:
(1)把25.72°用度、分、秒的形式表示;
(2)把45°12′30″化成度.
除不尽可以四舍五入取近似值
解:(1)因为0.72°=0.72×60′=43.2′,0.2×60″=12″,
所以25.72°=25°43′12″
(2)30× =0.5′,12.5× ≈0.21°,
所以45°12′30″≈45.21°.
探究一 角的单位换算与计算
合作探究
当堂检测
学习目标
课堂总结
自主学习
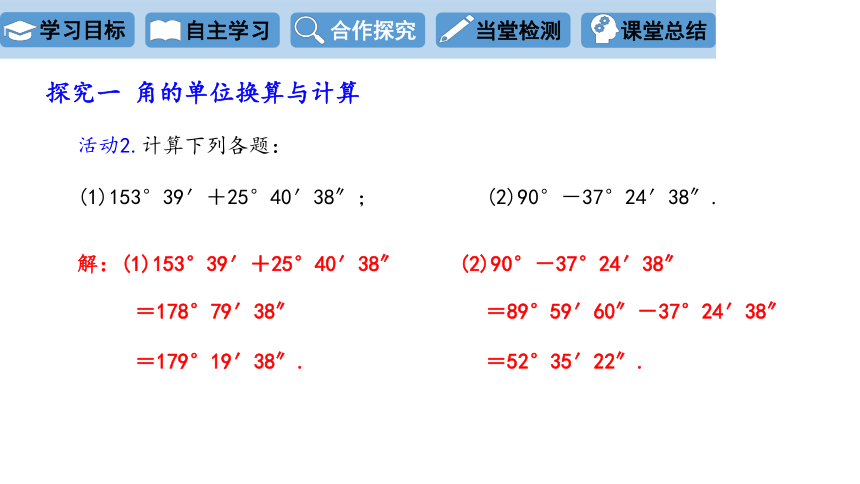
活动2.计算下列各题:
(1)153°39′+25°40′38″; (2)90°-37°24′38″.
解:(1)153°39′+25°40′38″
=178°79′38″
=179°19′38″.
(2)90°-37°24′38″
=89°59′60″-37°24′38″
=52°35′22″.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
在进行度、分、秒的和差计算时,要注意以下几点:
①度、分、秒均是60进制的;
②加、减法的运算,可以本着“度与度加减、分与分加减、秒与秒加减,不够减的时候借位”的原则.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.填空:
(1)0.65°= ′;
(2)32.43°= ° ′ ″ ;
(3)120°36′54″= °;
(4)108°42′36″= °.
39
32
25
48
120.615
108.71
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
(1) 120°-38°41′;
(2)67°31′+48°49′.
解:原式 = 119°60′-38°41′
= 81°19′ .
解:原式 = (67+48)°+(31+49)′
= 115°80′
= 116°20′ .
2.计算:
探究二 余角和补角的运算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:如图,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠BOD的度数.
(2)求∠DON的度数.
解:(1)∵ ∠AOC+ ∠AOD=180°,
∠BOD+ ∠AOD=180°且∠AOC=50°,
∴ ∠BOD=∠AOC=50°.(同角的补角相等)
因此,∠BOD的度数是50°.
探究二 余角和补角的运算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动4:如图,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(2)求∠DON的度数.
解:(2)∵ OM平分∠BOD 且∠BOD=50 °(已知)
∴∠DOM= ∠BOD= ×50°= 25°;
∵ ∠DON与∠DOM 互余,
∴ ∠DON = 90°-∠DOM =90°- 25° =65°.
因此, ∠DON的度数是65°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.如图,∠BOD=118°,∠AOD和∠AOC互余,OC平分∠AOB,求∠AOB的度数.
B
O
A
C
D
解:∵∠BOD=118°,∠AOD和∠AOC互余,
∴∠AOD+∠AOC=90°,
∠BOC=118°-90°=28°,
又∵OC平分∠AOB,
∴∠AOB=2∠BOC=2×28°=56°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.(1)已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是
.
(2)∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
150°
62°
28°
合作探究
当堂检测
学习目标
课堂总结
自主学习
(1) 12°36′56″+45°24′35″; (2) 79°45′+61°48′49″;
(3) 62°24′17″-45°13′26″; (4) 102°43′-87°26′49″.
2. 计算:
解:原式=58°1′31″
解:原式=141°33′49″
解:原式=17°10′51″
解:原式=102°42′60″-87°26′49″
=15°16′11″
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知一个角的补角是这个角的余角的 4倍,求这个角的度数.
解:设这个角为 x°,则它的余角是 ( 90-x )°,
补角是 ( 180-x )° .
根据题意,得
180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
合作探究
当堂检测
学习目标
课堂总结
自主学习
角的度量与计算
角的分类
角的单位换算与和、差计算
余角和补角的定义性质
周角
钝角
锐角
平角
直角
第四章 图形的认识
4.3.2 角的度量与计算
1.认识角的度量单位度、分、秒,会进行简单的换算.
2.了解余角、补角的概念,掌握余角和补角的性质.
3.会进行角的和、差计算,并能利用余角、补角的知识解决相关问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点一 角的度量单位
1. 叫做直角;
叫做锐角;
叫做钝角.
2.角的度量单位有 、 、 .进制是 .
3. 1°= ′,1′= ″,1°= ″,
1″= ′,1′= °,1周角= °,1平角= °.
平角的一半(即90°的角)
小于直角(即小于90°)的角
大于直角但小于平角(即大于90°但小于180°)的角
度
分
秒
60
60
60
3600
360
180
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点二 余角和补角的定义和性质
1.互为余角和互为补角的概念:
两角之和等于 度,这样的两个角互为余角.
两角之和等于 度,这样的两个角互为补角.
(1)若∠1和∠2互补,则∠1+∠2= ;
(2)若∠3和∠4互余,则∠3+∠4= .
90
180
180°
90°
3
4
1
2
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点二 余角和补角的定义和性质
2.互为余角及互为补角的性质:
同角或等角的余角 ;同角或等角的补角 .
应用举例:∵∠1=∠2,∠1+∠3=90°,∠2+∠4=90°(已知),
∴∠3=∠4(等角的余角相等)
填理由:∵∠1+∠2=180°,∠1+∠3=180°( )
∴∠3=∠4( )
相等
相等
已知
同角的补角相等
探究一 角的单位换算与计算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1.将下列角度进行换算:
(1)把25.72°用度、分、秒的形式表示;
(2)把45°12′30″化成度.
除不尽可以四舍五入取近似值
解:(1)因为0.72°=0.72×60′=43.2′,0.2×60″=12″,
所以25.72°=25°43′12″
(2)30× =0.5′,12.5× ≈0.21°,
所以45°12′30″≈45.21°.
探究一 角的单位换算与计算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2.计算下列各题:
(1)153°39′+25°40′38″; (2)90°-37°24′38″.
解:(1)153°39′+25°40′38″
=178°79′38″
=179°19′38″.
(2)90°-37°24′38″
=89°59′60″-37°24′38″
=52°35′22″.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
在进行度、分、秒的和差计算时,要注意以下几点:
①度、分、秒均是60进制的;
②加、减法的运算,可以本着“度与度加减、分与分加减、秒与秒加减,不够减的时候借位”的原则.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.填空:
(1)0.65°= ′;
(2)32.43°= ° ′ ″ ;
(3)120°36′54″= °;
(4)108°42′36″= °.
39
32
25
48
120.615
108.71
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
(1) 120°-38°41′;
(2)67°31′+48°49′.
解:原式 = 119°60′-38°41′
= 81°19′ .
解:原式 = (67+48)°+(31+49)′
= 115°80′
= 116°20′ .
2.计算:
探究二 余角和补角的运算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:如图,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠BOD的度数.
(2)求∠DON的度数.
解:(1)∵ ∠AOC+ ∠AOD=180°,
∠BOD+ ∠AOD=180°且∠AOC=50°,
∴ ∠BOD=∠AOC=50°.(同角的补角相等)
因此,∠BOD的度数是50°.
探究二 余角和补角的运算
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动4:如图,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(2)求∠DON的度数.
解:(2)∵ OM平分∠BOD 且∠BOD=50 °(已知)
∴∠DOM= ∠BOD= ×50°= 25°;
∵ ∠DON与∠DOM 互余,
∴ ∠DON = 90°-∠DOM =90°- 25° =65°.
因此, ∠DON的度数是65°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.如图,∠BOD=118°,∠AOD和∠AOC互余,OC平分∠AOB,求∠AOB的度数.
B
O
A
C
D
解:∵∠BOD=118°,∠AOD和∠AOC互余,
∴∠AOD+∠AOC=90°,
∠BOC=118°-90°=28°,
又∵OC平分∠AOB,
∴∠AOB=2∠BOC=2×28°=56°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.(1)已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是
.
(2)∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
150°
62°
28°
合作探究
当堂检测
学习目标
课堂总结
自主学习
(1) 12°36′56″+45°24′35″; (2) 79°45′+61°48′49″;
(3) 62°24′17″-45°13′26″; (4) 102°43′-87°26′49″.
2. 计算:
解:原式=58°1′31″
解:原式=141°33′49″
解:原式=17°10′51″
解:原式=102°42′60″-87°26′49″
=15°16′11″
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知一个角的补角是这个角的余角的 4倍,求这个角的度数.
解:设这个角为 x°,则它的余角是 ( 90-x )°,
补角是 ( 180-x )° .
根据题意,得
180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
合作探究
当堂检测
学习目标
课堂总结
自主学习
角的度量与计算
角的分类
角的单位换算与和、差计算
余角和补角的定义性质
周角
钝角
锐角
平角
直角
同课章节目录
