第四章 图形的认识 复习课件 21张PPT 2023—2024学年湘教版数学七年级上册
文档属性
| 名称 | 第四章 图形的认识 复习课件 21张PPT 2023—2024学年湘教版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 21:42:56 | ||
图片预览




文档简介
(共21张PPT)
第四章 图形的认识
复习课
1.理解几何图形的概念,并能对具体图形进行识别或判断.
2.知道线段、射线、直线、角的表示方法,并会进行度、分、秒的换算.
3.知道线段中点及角平分线的含义,并会进行相关的计算
4.熟记两个基本事实,并能应用它们解决实际问题
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
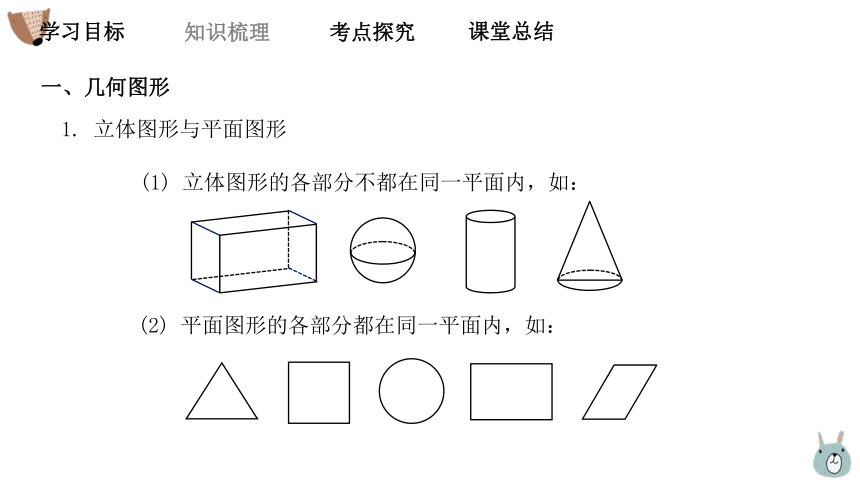
一、几何图形
1. 立体图形与平面图形
(1) 立体图形的各部分不都在同一平面内,如:
(2) 平面图形的各部分都在同一平面内,如:
考点探究
学习目标
课堂总结
知识梳理
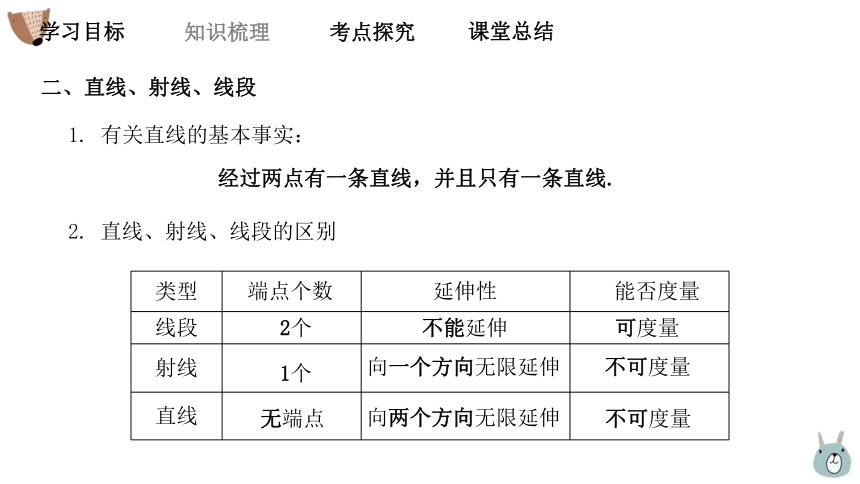
二、直线、射线、线段
1. 有关直线的基本事实:
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
考点探究
学习目标
课堂总结
知识梳理
3. 基本作图
(1) 作一线段等于已知线段;
(2)利用尺规作图作一条线段等于两条线段的和、差.
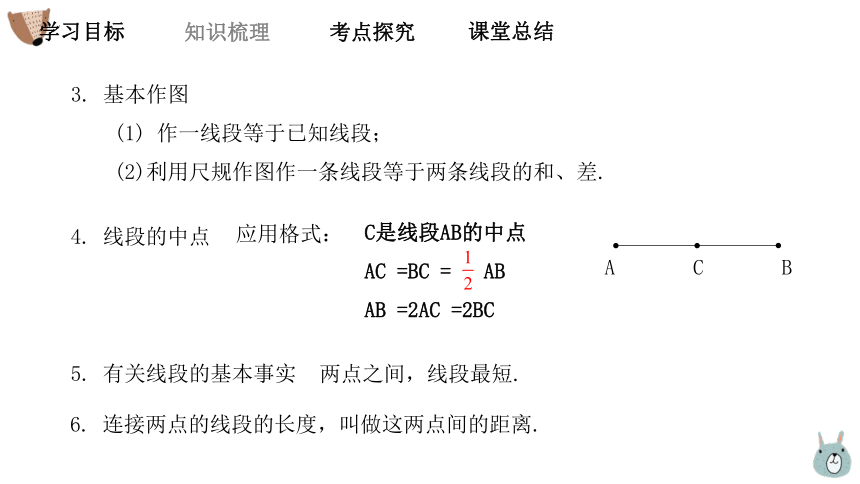
4. 线段的中点
应用格式:
A
C
B
C是线段AB的中点
AC =BC = AB
AB =2AC =2BC
5. 有关线段的基本事实
两点之间,线段最短.
6. 连接两点的线段的长度,叫做这两点间的距离.
考点探究
学习目标
课堂总结
知识梳理
三、角
1. 角的定义
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2. 角的度量
度、分、秒的互化
1°=60′,1′=60″, ,
考点探究
学习目标
课堂总结
知识梳理
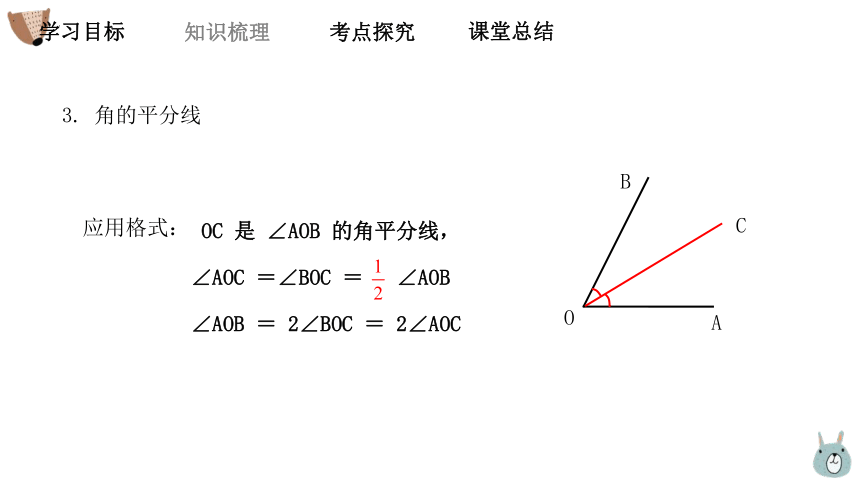
3. 角的平分线
O
B
A
C
应用格式:
OC 是 ∠AOB 的角平分线,
∠AOC =∠BOC = ∠AOB
∠AOB = 2∠BOC = 2∠AOC
考点探究
学习目标
课堂总结
知识梳理
4. 余角和补角
(1) 定义
(2) 性质
① 同角 (或等角) 的补角相等;② 同角 (或等角) 的余角相等
① 如果两个角的和等于90° (直角),就说这两个角互为余角
( 简称为互余 ).
② 如果两个角的和等于180°(平角),就说这两个角互为补角
( 简称为互补 ).
考点探究
学习目标
课堂总结
知识梳理
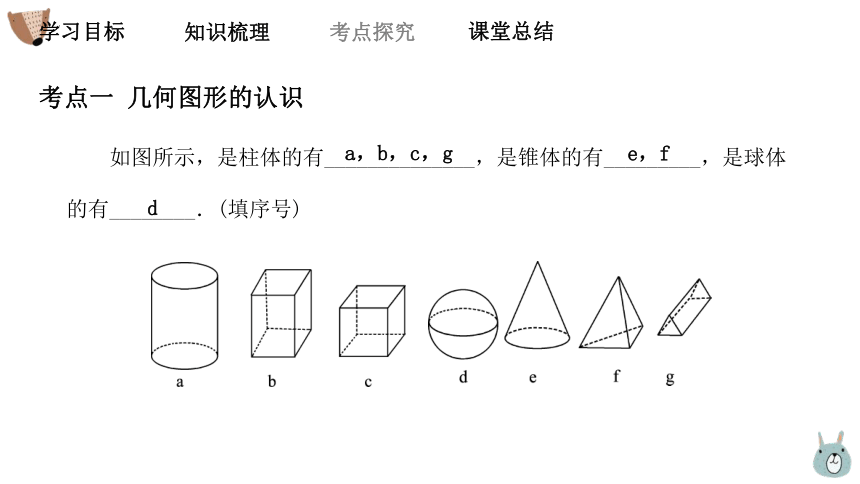
考点一 几何图形的认识
如图所示,是柱体的有______________,是锥体的有_________,是球体的有________.(填序号)
a,b,c,g
d
e,f
考点探究
学习目标
课堂总结
知识梳理
归纳总结:
柱体
圆柱:上下底面平行且为圆面,侧面是曲面.
棱柱:上下底面平行且为能重合的多边形,侧面是长方形.
锥体
圆锥:底面是圆,侧面是曲面
棱锥:底面是多边形,侧面是三角形
只有一个底面
考点探究
学习目标
课堂总结
知识梳理
针对训练
1.下面物体中,最接近圆柱的是( )
C
考点探究
学习目标
课堂总结
知识梳理
考点二 线段长度的计算
如图所示,AD= DB,E是BC的中点,BE= AC=2cm,求线段DE的长.
解:因为E是BC的中点,
所以BE=EC=2cm,BC=2BE=4cm,
又因为AC=5BE=10cm.
所以AB=AC-BC=10-4=6cm,
且AB=AD+BD=AD+2AD=3AD,
所以AD=2cm,BD=4cm,
DE=DB+BE=4+2=6cm.
考点探究
学习目标
课堂总结
知识梳理
针对训练
2. 已知:点 A,B,C 在一直线上,AB =12 cm,BC =4 cm. 点 M,N分别是线段 AB,BC 的中点. 求线段 MN 的长度.
A M C N B
图①
∴ BM = AB = ×12 = 6 (cm),BN = BC = ×4 = 2 (cm),
解:如图①,当 C 在 AB 间时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM-BN = 6-2 = 4 (cm).
考点探究
学习目标
课堂总结
知识梳理
针对训练
2. 已知:点 A,B,C 在一直线上,AB =12 cm,BC =4 cm. 点 M,N分别是线段 AB,BC 的中点. 求线段 MN 的长度.
C
A
M
N
B
图②
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当C在线段AB外时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM + BN = 6 + 2 = 8 (cm).
考点探究
学习目标
课堂总结
知识梳理
考点三 关于线段的基本事实
如图,是一个三级台阶,A 和 B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到 B 点去吃可口的食物. 若这只蚂蚁从 A 点出发,沿着台阶面爬到B 点,你能画出蚂蚁爬行的最短路线吗?
考点探究
学习目标
课堂总结
知识梳理
解:如图,将台阶面展开成平面图形.
连接 AB 两点,
因为两点之间线段最短,
所以线段AB 为蚂蚁爬行的最短路线.
A
B
考点探究
学习目标
课堂总结
知识梳理
针对训练
B
B
3. 如图,在A点有一只壁虎,要沿着圆柱体的表面爬到B点去吃蚊子. 请画出壁虎在圆柱体表面爬行的最短路线.
考点探究
学习目标
课堂总结
知识梳理
考点四 角的和、差计算
计算: (1)28°32′46″+15°36′48″; (2)30°-23′40″.
解:(1)28°32′46″+15°36′48″
=43°68′94″
=44°9′34″.
(2)30°-23′40″
=29°59′60″-23′40″
=29°36′20″.
考点探究
学习目标
课堂总结
知识梳理
针对训练
4.计算:
(1)48°39′+67°31′; (2)180°﹣21°17′.
解:(1)原式=116°10′;
(2)原式=158°43′.
考点探究
学习目标
课堂总结
知识梳理
考点五 余角和补角
问题:已知∠α和∠β互为补角,并且∠β的一半比∠α小30°,求∠α,∠β.
解:设∠α=x°,则∠β=180°-x°.
根据题意 ∠β=2(∠α-30°),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80°,∠β=100°.
提示:此题和差倍分关系较复杂,可列方程解答.
考点探究
学习目标
课堂总结
知识梳理
几何图形
立体图形和平面图形
平面图形
直线、射线、线段
角
表示方法
线段长短的比较与计算
两个基本事实
中点
表示方法
角的度量、比较与计算
余角和补角
角平分线
概念、性质
第四章 图形的认识
复习课
1.理解几何图形的概念,并能对具体图形进行识别或判断.
2.知道线段、射线、直线、角的表示方法,并会进行度、分、秒的换算.
3.知道线段中点及角平分线的含义,并会进行相关的计算
4.熟记两个基本事实,并能应用它们解决实际问题
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
一、几何图形
1. 立体图形与平面图形
(1) 立体图形的各部分不都在同一平面内,如:
(2) 平面图形的各部分都在同一平面内,如:
考点探究
学习目标
课堂总结
知识梳理
二、直线、射线、线段
1. 有关直线的基本事实:
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
考点探究
学习目标
课堂总结
知识梳理
3. 基本作图
(1) 作一线段等于已知线段;
(2)利用尺规作图作一条线段等于两条线段的和、差.
4. 线段的中点
应用格式:
A
C
B
C是线段AB的中点
AC =BC = AB
AB =2AC =2BC
5. 有关线段的基本事实
两点之间,线段最短.
6. 连接两点的线段的长度,叫做这两点间的距离.
考点探究
学习目标
课堂总结
知识梳理
三、角
1. 角的定义
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2. 角的度量
度、分、秒的互化
1°=60′,1′=60″, ,
考点探究
学习目标
课堂总结
知识梳理
3. 角的平分线
O
B
A
C
应用格式:
OC 是 ∠AOB 的角平分线,
∠AOC =∠BOC = ∠AOB
∠AOB = 2∠BOC = 2∠AOC
考点探究
学习目标
课堂总结
知识梳理
4. 余角和补角
(1) 定义
(2) 性质
① 同角 (或等角) 的补角相等;② 同角 (或等角) 的余角相等
① 如果两个角的和等于90° (直角),就说这两个角互为余角
( 简称为互余 ).
② 如果两个角的和等于180°(平角),就说这两个角互为补角
( 简称为互补 ).
考点探究
学习目标
课堂总结
知识梳理
考点一 几何图形的认识
如图所示,是柱体的有______________,是锥体的有_________,是球体的有________.(填序号)
a,b,c,g
d
e,f
考点探究
学习目标
课堂总结
知识梳理
归纳总结:
柱体
圆柱:上下底面平行且为圆面,侧面是曲面.
棱柱:上下底面平行且为能重合的多边形,侧面是长方形.
锥体
圆锥:底面是圆,侧面是曲面
棱锥:底面是多边形,侧面是三角形
只有一个底面
考点探究
学习目标
课堂总结
知识梳理
针对训练
1.下面物体中,最接近圆柱的是( )
C
考点探究
学习目标
课堂总结
知识梳理
考点二 线段长度的计算
如图所示,AD= DB,E是BC的中点,BE= AC=2cm,求线段DE的长.
解:因为E是BC的中点,
所以BE=EC=2cm,BC=2BE=4cm,
又因为AC=5BE=10cm.
所以AB=AC-BC=10-4=6cm,
且AB=AD+BD=AD+2AD=3AD,
所以AD=2cm,BD=4cm,
DE=DB+BE=4+2=6cm.
考点探究
学习目标
课堂总结
知识梳理
针对训练
2. 已知:点 A,B,C 在一直线上,AB =12 cm,BC =4 cm. 点 M,N分别是线段 AB,BC 的中点. 求线段 MN 的长度.
A M C N B
图①
∴ BM = AB = ×12 = 6 (cm),BN = BC = ×4 = 2 (cm),
解:如图①,当 C 在 AB 间时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM-BN = 6-2 = 4 (cm).
考点探究
学习目标
课堂总结
知识梳理
针对训练
2. 已知:点 A,B,C 在一直线上,AB =12 cm,BC =4 cm. 点 M,N分别是线段 AB,BC 的中点. 求线段 MN 的长度.
C
A
M
N
B
图②
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当C在线段AB外时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM + BN = 6 + 2 = 8 (cm).
考点探究
学习目标
课堂总结
知识梳理
考点三 关于线段的基本事实
如图,是一个三级台阶,A 和 B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到 B 点去吃可口的食物. 若这只蚂蚁从 A 点出发,沿着台阶面爬到B 点,你能画出蚂蚁爬行的最短路线吗?
考点探究
学习目标
课堂总结
知识梳理
解:如图,将台阶面展开成平面图形.
连接 AB 两点,
因为两点之间线段最短,
所以线段AB 为蚂蚁爬行的最短路线.
A
B
考点探究
学习目标
课堂总结
知识梳理
针对训练
B
B
3. 如图,在A点有一只壁虎,要沿着圆柱体的表面爬到B点去吃蚊子. 请画出壁虎在圆柱体表面爬行的最短路线.
考点探究
学习目标
课堂总结
知识梳理
考点四 角的和、差计算
计算: (1)28°32′46″+15°36′48″; (2)30°-23′40″.
解:(1)28°32′46″+15°36′48″
=43°68′94″
=44°9′34″.
(2)30°-23′40″
=29°59′60″-23′40″
=29°36′20″.
考点探究
学习目标
课堂总结
知识梳理
针对训练
4.计算:
(1)48°39′+67°31′; (2)180°﹣21°17′.
解:(1)原式=116°10′;
(2)原式=158°43′.
考点探究
学习目标
课堂总结
知识梳理
考点五 余角和补角
问题:已知∠α和∠β互为补角,并且∠β的一半比∠α小30°,求∠α,∠β.
解:设∠α=x°,则∠β=180°-x°.
根据题意 ∠β=2(∠α-30°),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80°,∠β=100°.
提示:此题和差倍分关系较复杂,可列方程解答.
考点探究
学习目标
课堂总结
知识梳理
几何图形
立体图形和平面图形
平面图形
直线、射线、线段
角
表示方法
线段长短的比较与计算
两个基本事实
中点
表示方法
角的度量、比较与计算
余角和补角
角平分线
概念、性质
同课章节目录
