图形的旋转

课件39张PPT。 23.1 图形的旋转
数学欣赏ABDHGEFIJKLC数学欣赏数学欣赏

平移的定义
将一个图形沿着一定的方向移动
一定的距离的图形变换 动态演示OP′P点O是旋转中心
∠ POP′或120°是旋转角
点P与 P′是对应点
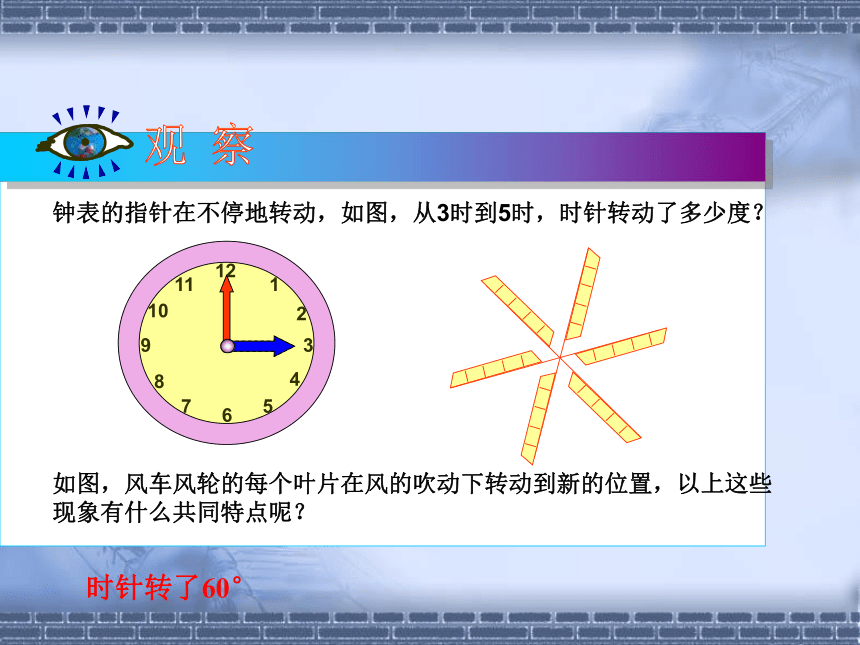
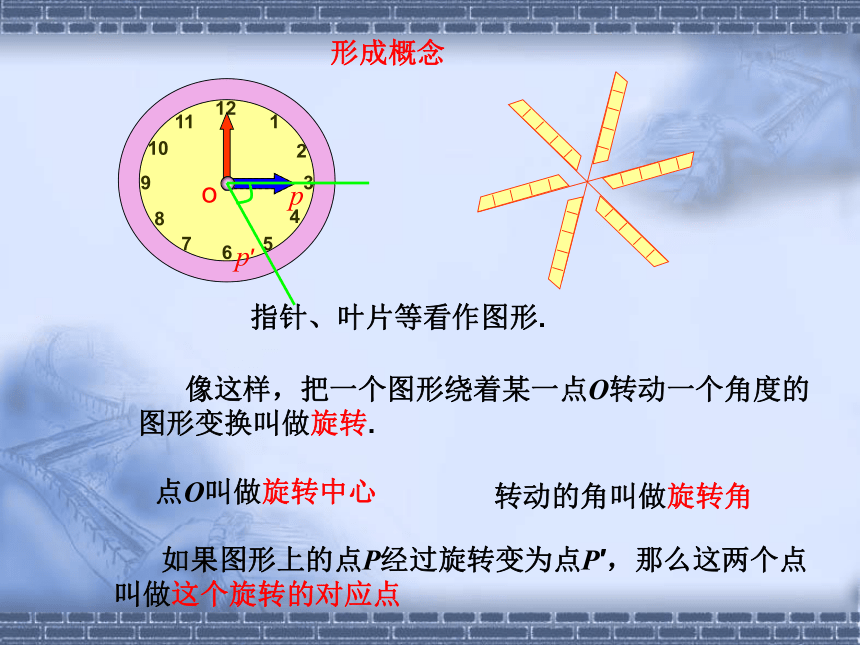
自学课本自学内容：如何确定旋转中心、旋转角、对应点1.举出一些现实生活中旋转的实例，并指出旋转中心和旋转角.练习观 察钟表的指针在不停地转动，如图，从3时到5时，时针转动了多少度？如图，风车风轮的每个叶片在风的吹动下转动到新的位置，以上这些现象有什么共同特点呢？时针转了60°指针、叶片等看作图形. 像这样，把一个图形绕着某一点O转动一个角度的
图形变换叫做旋转. 点O叫做旋转中心 如果图形上的点P经过旋转变为点P′，那么这两个点
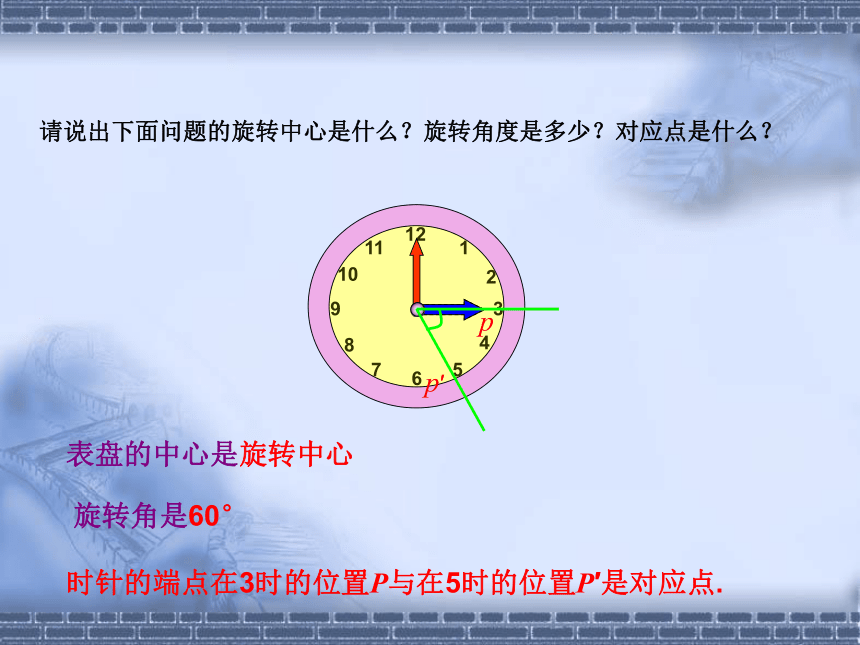
叫做这个旋转的对应点opp′转动的角叫做旋转角形成概念时针的端点在3时的位置P与在5时的位置P′是对应点.pp′请说出下面问题的旋转中心是什么？旋转角度是多少？对应点是什么？表盘的中心是旋转中心旋转角是60° 2.时钟的时针在不停地旋转，从上午6时到上午9时，时针旋转的旋转角是多少度？从上午9时到上午10时呢？旋转角度是90°旋转角度是30°在硬纸板上，挖一个三角形洞，再挖一个小洞O作为旋转中心，硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案（△ABC）然后围绕旋转中心转动硬纸板，再描出这个挖掉的三角形（△A′B′C′） ，移开硬纸板。
线段OA与OA′有什么关系？∠AOA′与∠BOB′有什么关系？ △ABC与△A′B′C′形状和大小有什么关系？ABCOOA=OA′∠AOA′=∠BOB′△ABC≌△A′B′C′对应点与旋转中心所连线段的夹角等于旋转角.旋转前、后的图形全等.对应点到旋转中心的距离相等.因此，在CB的延长线上取点E′，使BE′=DE，则△ABE′为旋转后的图形.ABCDEE′如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.分析：关键是确定△ADE三个顶点的对应点，即它们旋转后的位置.解：因为点A是旋转中心，所以它的对应点是它本身。正方形ABCD中，AD=AB， ∠DAB=90°，所以旋转后点D与B重合.设点E的对应点为点E′，因为旋转后的图形与旋转前的图形全等，所以∠ABE′= ∠ADE=90°，BE′=DE还有别的办法吗？例
1.如图，小明坐在秋千上，秋千旋转了80°，请在图中小明身上任意选一点P，利用旋转性质，标出点P的对应点.PP′2.如图，用左面的三角形经过怎样的旋转，可以得到右面的图形？3.找出图中扳手拧螺母时的旋转中心和旋转角。O旋转中心为螺母的中心旋转角为∠POP′PP′oaoa1.旋转中心不变，改变旋转角（如图）把一个图案（如图）进行旋转，选择不同的旋转中心， 不同的旋转角，会出现不同的效果.图案的旋转3. 美丽的图案是这样形成的我们学过平移、轴对称和旋转，我们可以利用这些图形变换中的一种进行图案设计，还可以利用这些图形变换的组合进行图案设计。例如，图中的图案就是由 经过旋转、轴对称和平移得到的。以点O为旋转中心将 逆时针旋转90°三次作出图，然后以L为对称轴作出图。平移图就可以作出图中的图案。（2）改变三角形的形状，看看旋转的效果.猜想：旋转的性质
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角 请设计一种方案，
验证关于旋转性质的猜想是否正确
旋转的性质：
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转前、后的图形全等例1．如图，△ABC是等边三角形，D是BC边上一点，△ABD经过旋转后到达△ACE的位置．
（1）旋转中心是哪一点？旋转了多少度？
（2）如果M是AB的中点，那么经过上述旋转后，点M的对应点点F在什么位置？解:（1）旋转中心是点A，旋转了60°（2）点F是AC的中点学以致用F.练习1．如下图，这个图案可以看作是哪个“基本图形”经过怎样旋转组合得到的，你能想到几种“基本图形”？学以致用答案有很多啦练习2：动手实践
利用旋转，请设计一个优美的图案，给它取个名字，并说出它的含义。
学以致用电脑设计旋转图案旋转图案欣赏旋转图案欣赏旋转图案欣赏旋转图案欣赏
旋转的概念
旋转的性质
感受数学之美
从数学的角度认识生活，勇于探究
课堂小结
1 ．课本66页第1题、第4题.
2 ．课后上网搜索有关旋转的图片和动画，
下节课进行展示. 课后作业当电梯将你送到门前当帆船驶入平静的港湾当乘坐索道观光游览当面对车间的流水线你可曾想到平移就在你身边当风车不停地转当木马带你飞旋当车轮的速度追赶着极限
你可曾感到旋转与我们息息相关精彩的平移与旋转让我们的生活一片灿烂！美丽的平移与旋转谢谢指导！