浙江省杭州市萧山区重点中学2023-2024学年高一上学期12月月考数学试卷(含答案)
文档属性
| 名称 | 浙江省杭州市萧山区重点中学2023-2024学年高一上学期12月月考数学试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 242.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 00:00:00 | ||
图片预览



文档简介
萧山区重点中学2023级高一数学12月月考
一.、单选题(每题3分,共24分)
1.学校开运动会,设A={x|x是参加100米跑的同学},B={x|x是参加200米跑的同学},C={x|x是参加400米跑的同学}.学校规定,每个参加上述比赛的同学最多只能参加两项比赛.请你用集合的运算说明这项规定( )
A.(A∩B)∪C= B.(A∪B)∩C= C.(A∪B)∪C= D.(A∩B)∩C=
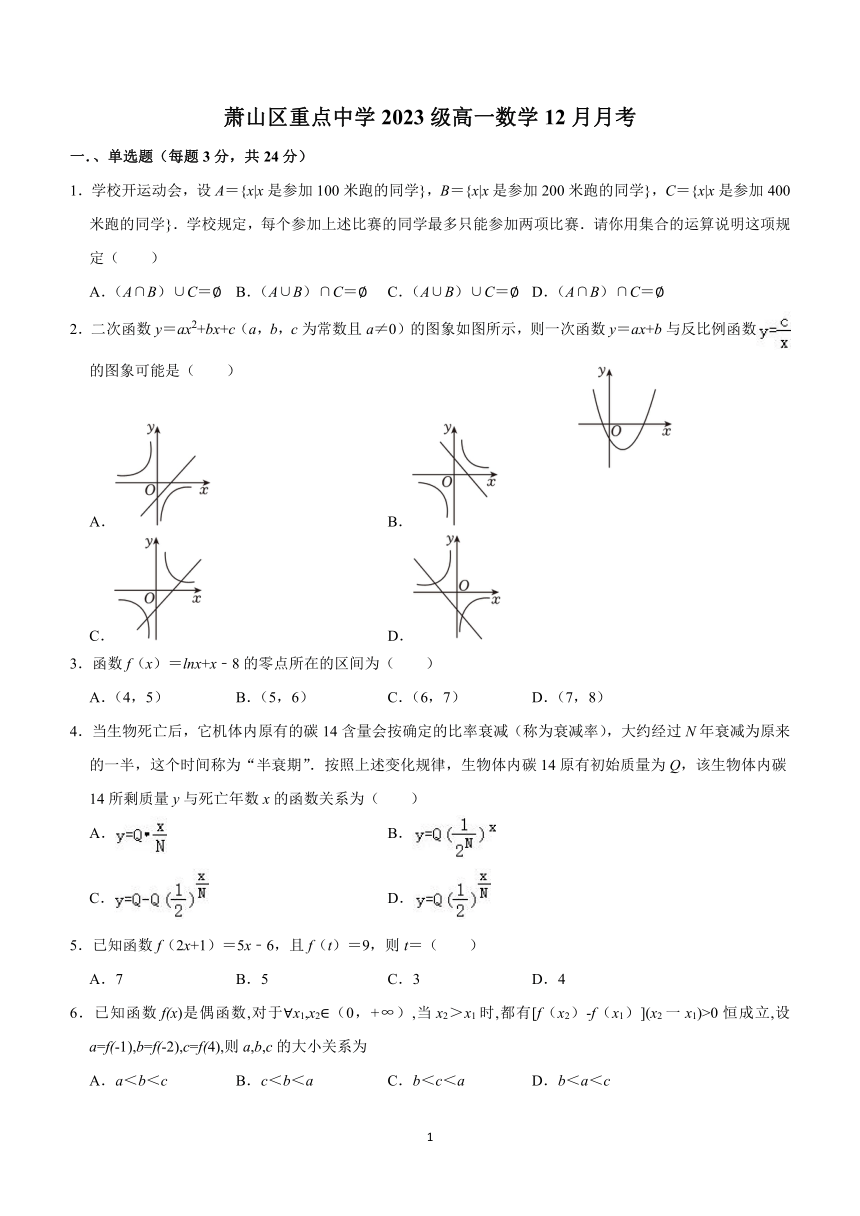
2.二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数的图象可能是( )
A. B.
C. D.
3.函数f(x)=lnx+x﹣8的零点所在的区间为( )
A.(4,5) B.(5,6) C.(6,7) D.(7,8)
4.当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约经过N年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14原有初始质量为Q,该生物体内碳14所剩质量y与死亡年数x的函数关系为( )
A. B.
C. D.
5.已知函数f(2x+1)=5x﹣6,且f(t)=9,则t=( )
A.7 B.5 C.3 D.4
6.已知函数f(x)是偶函数,对于 x1,x2∈(0,+∞),当x2>x1时,都有[f(x2)-f(x1)](x2一x1)>0恒成立,设a=f(-1),b=f(-2),c=f(4),则a,b,c的大小关系为
A.a<b<c B.c<b<a C.b<c<a D.b<a<c
7.已知函数,且f(a)=10,那么f(﹣a)等于( )
A.﹣18 B.﹣26 C.﹣10 D.10
8.已知函数f(x)=,当f(n)=f(m)且n≠m时,则|n﹣m|的最小值为( )
A.3 B. C.2 D.
二、多选题(每题4分,共16分,错选多选不选得0分,少选得2分)
9.下列函数中,值域是(0,+∞)的是( )
A.y=2﹣x B.y= C.y=ln(ex+1) D.y=
10.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1,x2,且x1<x2,则下列结论正确的是( )
A.当m=0时,x1=2,x2=3
B.
C.当m>0时,2<x1<x2<3
D.二次函数y=(x﹣x1)(x﹣x2)+m的零点为2和3
11.下列说法不正确的是( )
A.命题“ x<1,都有x2<1”的否定是“ x≥1,使得x2≥1”
B.集合A={﹣2,1},B={x|ax=2},若A B=B,则实数a的取值集合为{﹣1,2}
C.方程3x2+a(a﹣6)x﹣3=0有一个根大于1,另一个根小于1的充要条件是0<a<6
D.若存在x∈[,2]使等式x2﹣2x﹣m<0上能成立,则实数m的取值范围(0,+∞)
12.设a=log68+log86,6a+8a=10b,则( )
A.a>2 B.a>b C.b>2 D.2>b
三.填空题(每题4分,共16分)
13.已知幂函数f(x)=(m2+m﹣5)xm在(0,+∞)上单调递减,则m= .
14.已知函数f(x)是定义在[﹣3,2m+1]上的偶函数,则m= ;
15.不等式2<()3(x﹣1)的解集为 .
16.已知函数f(x)=,若f(x)的值域为x∈[1,5],则实数c的取值范围是 .
四.解答题(第17题8分,第18题,19题每题10分,第20、21、22题每题12分,共64分)
17.计算:(1)﹣(e﹣1)0++×
(2)lg100++25﹣32·3
18.已知函数f(x)=ax2+bx+c(a≠0).
(1)若b=a,c=﹣2,不等式f(x)<0对一切实数x都成立,求a的取值范围;
(2)若f(x)>0的解集为(﹣2,1),求关于x的不等式cx2+bx+a>0的解集.
19.为促进旅游事业的发展,我市某著名景点推出“一费全包,团体打折”的团体票方案:
(1)只要一次购票即可游玩景点内所有项目且能当天无限次乘坐园内观光车;
(2)当团体不超过40人时,人均收费100元;超过40人且不超过m人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队时,收取总费用为y元.
(i)当40<m≤100时,求y关于x的函数表达式y=f(x);
(ii)若m设置不合理,有可能出现团体人数增加而收取的总费用反而减少这一现象.要令收取的总费用总随着团队中人数的增加而增加,求m的取值范围.
20.已知函数.
(1)求的值;
(2)设函数g(x)=f(x)+2,证明:g(x)在(1,+∞)上有唯一零点.
21.设函数f(x)=ax﹣ka﹣x(a>0且a≠1,k∈R),f(x)是定义域为R的奇函数.
(1)求k的值,判断当a>1时,函数f(x)在R上的单调性并用定义法证明;
(2)若,函数g(x)=a2x+a﹣2x﹣f(x),x∈[﹣1,1]求g(x)的值域.
22.设函数f(x)=logax(a>0≡a≠1).
(1)解关于a的不等式f(7﹣2a)≤f(5a);
(2)若恒成立,则是否存在实数k,令x∈[0,1]时,恒有f(4x+3)﹣f(k 2x+1)<0?若存在,求实数k的范围;若不存在,请说明理由.
参考答案
一.选择题(共8小题)
1 2 3 4 5 6 7 8
D A C D A A B C
二.多选题(共4小题)
9 10 11 12
ABC ABD ABD ABC
三.填空题(共4小题)
13 14 15 16
﹣3 1 (﹣2,3) [﹣1,﹣]
四.解答题(共6小题)
17.解:(1)11
(2)4
18解:(1)当b=a,c=﹣2时,不等式f(x)<0可化为ax2+ax﹣2<0,
即ax2+ax﹣2<0对一切实数x都成立,
则,解得﹣8<a<0,
即a的取值范围为(﹣8,0);
(2)由于f(x)>0的解集为(﹣2,1),
所以﹣2和1是方程ax2+bx+c=0的两个根,
所以,
即,所以,
所以不等式cx2+bx+a>0,即﹣2ax2+ax+a>0,
所以2x2﹣x﹣1>0,
即(2x+1)(x﹣1)>0,
解得x<﹣或x>1,
即不等式cx2+bx+a>0的解集为.
19.解:(i)当0<x≤40时,y=100x;
当40<x≤m时,y=[100﹣(x﹣40)]x=﹣x2+140x,(40<m≤100);
x>m时,y=(140﹣m)x.
所以y=f(x)=.
(ii)①当0<x≤40时,y=100x,y随x增大而增大,
②当40<m≤100时,140﹣m>0.
所以y=(140﹣m)x,y随x增大而增大.
当40<x≤m时,
y=﹣x2+140x=﹣(x﹣70)2+4900,
所以当40<x≤70时,y随x增大而增大;当x>70时,y随x增大而减小.
所以当40<x≤70时,y=﹣(x﹣70)2+4900,y随x增大而增大.
综上所述,当40<m≤70时,景点收取的总费用随着团队中人数增加而增加.
20.解:(1)因为,
所以.
(2)证明:,
因为函数y=lgx在(1,+∞)上单调递增,
函数在(1,+∞)上单调递增,
所以g(x)在(1,+∞)上单调递增,
又因为,
,
所以g(10) g(100)<0,
所以 x0∈(10,100),g(x0)=0,即g(x)在(1,+∞)上有且仅有一个零点.
21.解:(1)f(x)是定义域为R的奇函数,则f(0)=0,
∴k=1,f(x)在R上单调递增,
任取x1<x2,
则f(x1)﹣f(x2)=﹣﹣+
=()(1+)
由于a>1,x1<x2,
则,,
得f(x1)﹣f(x2)<0,f(x)在R上单调递增,得证;
(2),得a=2,
g(x)=a2x+a﹣2x﹣f(x)=22x+2﹣2x﹣(2x﹣2﹣x)=(2x﹣2﹣x)2﹣(2x﹣2﹣x)+2,
令t=f(x)=2x﹣2﹣x,由(1)知f(x)为增函数,x∈[﹣1,1],,
设,
当t=时,函数取得最小值,当t=﹣时,函数取得最大值,
故函数的值域为.
22解:(1)当0<a<1时,不等式f(7﹣2a)≤f(5a) ,
解得0<a<1;
当a>1时,不等式f(7﹣2a)≤f(5a) ,
解得1<a<.
综上所述,不等式的解集为(0,1)∪(1,).
(2)存在k>2使f(4x+3)﹣f(k 2x+1)<0在[0,1]上恒成立.
因为m2+1>0,所以
,
当且仅当,即m=0时取等号,
又由恒成立,可知f(x)为增函数,所以a>1,
f(4x+3)﹣f(k 2x+1)<0在x∈[0,1]时恒成立,
即f(4x+3)<f(k 2x+1)在x∈[0,1]时恒成立,
即4x+3<k 2x+1在x∈[0,1]时恒成立,
即=在x∈[0,1]时恒成立,
令t=2x,因为x∈[0,1],所以t∈[1,2],
g(t)=在[1,]上单调递减,在[,2]上单调递增,
且g(1)=2,g(2)=,
所以g(t)在[1,2]上的最大值为2,
即的最大值为2,所以存在k>2使f(4x+3)﹣f(k 2x+1)<0在[0,1]上恒成立.
所以k的取值范围是[2,+∞).
一.、单选题(每题3分,共24分)
1.学校开运动会,设A={x|x是参加100米跑的同学},B={x|x是参加200米跑的同学},C={x|x是参加400米跑的同学}.学校规定,每个参加上述比赛的同学最多只能参加两项比赛.请你用集合的运算说明这项规定( )
A.(A∩B)∪C= B.(A∪B)∩C= C.(A∪B)∪C= D.(A∩B)∩C=
2.二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数的图象可能是( )
A. B.
C. D.
3.函数f(x)=lnx+x﹣8的零点所在的区间为( )
A.(4,5) B.(5,6) C.(6,7) D.(7,8)
4.当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约经过N年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14原有初始质量为Q,该生物体内碳14所剩质量y与死亡年数x的函数关系为( )
A. B.
C. D.
5.已知函数f(2x+1)=5x﹣6,且f(t)=9,则t=( )
A.7 B.5 C.3 D.4
6.已知函数f(x)是偶函数,对于 x1,x2∈(0,+∞),当x2>x1时,都有[f(x2)-f(x1)](x2一x1)>0恒成立,设a=f(-1),b=f(-2),c=f(4),则a,b,c的大小关系为
A.a<b<c B.c<b<a C.b<c<a D.b<a<c
7.已知函数,且f(a)=10,那么f(﹣a)等于( )
A.﹣18 B.﹣26 C.﹣10 D.10
8.已知函数f(x)=,当f(n)=f(m)且n≠m时,则|n﹣m|的最小值为( )
A.3 B. C.2 D.
二、多选题(每题4分,共16分,错选多选不选得0分,少选得2分)
9.下列函数中,值域是(0,+∞)的是( )
A.y=2﹣x B.y= C.y=ln(ex+1) D.y=
10.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1,x2,且x1<x2,则下列结论正确的是( )
A.当m=0时,x1=2,x2=3
B.
C.当m>0时,2<x1<x2<3
D.二次函数y=(x﹣x1)(x﹣x2)+m的零点为2和3
11.下列说法不正确的是( )
A.命题“ x<1,都有x2<1”的否定是“ x≥1,使得x2≥1”
B.集合A={﹣2,1},B={x|ax=2},若A B=B,则实数a的取值集合为{﹣1,2}
C.方程3x2+a(a﹣6)x﹣3=0有一个根大于1,另一个根小于1的充要条件是0<a<6
D.若存在x∈[,2]使等式x2﹣2x﹣m<0上能成立,则实数m的取值范围(0,+∞)
12.设a=log68+log86,6a+8a=10b,则( )
A.a>2 B.a>b C.b>2 D.2>b
三.填空题(每题4分,共16分)
13.已知幂函数f(x)=(m2+m﹣5)xm在(0,+∞)上单调递减,则m= .
14.已知函数f(x)是定义在[﹣3,2m+1]上的偶函数,则m= ;
15.不等式2<()3(x﹣1)的解集为 .
16.已知函数f(x)=,若f(x)的值域为x∈[1,5],则实数c的取值范围是 .
四.解答题(第17题8分,第18题,19题每题10分,第20、21、22题每题12分,共64分)
17.计算:(1)﹣(e﹣1)0++×
(2)lg100++25﹣32·3
18.已知函数f(x)=ax2+bx+c(a≠0).
(1)若b=a,c=﹣2,不等式f(x)<0对一切实数x都成立,求a的取值范围;
(2)若f(x)>0的解集为(﹣2,1),求关于x的不等式cx2+bx+a>0的解集.
19.为促进旅游事业的发展,我市某著名景点推出“一费全包,团体打折”的团体票方案:
(1)只要一次购票即可游玩景点内所有项目且能当天无限次乘坐园内观光车;
(2)当团体不超过40人时,人均收费100元;超过40人且不超过m人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队时,收取总费用为y元.
(i)当40<m≤100时,求y关于x的函数表达式y=f(x);
(ii)若m设置不合理,有可能出现团体人数增加而收取的总费用反而减少这一现象.要令收取的总费用总随着团队中人数的增加而增加,求m的取值范围.
20.已知函数.
(1)求的值;
(2)设函数g(x)=f(x)+2,证明:g(x)在(1,+∞)上有唯一零点.
21.设函数f(x)=ax﹣ka﹣x(a>0且a≠1,k∈R),f(x)是定义域为R的奇函数.
(1)求k的值,判断当a>1时,函数f(x)在R上的单调性并用定义法证明;
(2)若,函数g(x)=a2x+a﹣2x﹣f(x),x∈[﹣1,1]求g(x)的值域.
22.设函数f(x)=logax(a>0≡a≠1).
(1)解关于a的不等式f(7﹣2a)≤f(5a);
(2)若恒成立,则是否存在实数k,令x∈[0,1]时,恒有f(4x+3)﹣f(k 2x+1)<0?若存在,求实数k的范围;若不存在,请说明理由.
参考答案
一.选择题(共8小题)
1 2 3 4 5 6 7 8
D A C D A A B C
二.多选题(共4小题)
9 10 11 12
ABC ABD ABD ABC
三.填空题(共4小题)
13 14 15 16
﹣3 1 (﹣2,3) [﹣1,﹣]
四.解答题(共6小题)
17.解:(1)11
(2)4
18解:(1)当b=a,c=﹣2时,不等式f(x)<0可化为ax2+ax﹣2<0,
即ax2+ax﹣2<0对一切实数x都成立,
则,解得﹣8<a<0,
即a的取值范围为(﹣8,0);
(2)由于f(x)>0的解集为(﹣2,1),
所以﹣2和1是方程ax2+bx+c=0的两个根,
所以,
即,所以,
所以不等式cx2+bx+a>0,即﹣2ax2+ax+a>0,
所以2x2﹣x﹣1>0,
即(2x+1)(x﹣1)>0,
解得x<﹣或x>1,
即不等式cx2+bx+a>0的解集为.
19.解:(i)当0<x≤40时,y=100x;
当40<x≤m时,y=[100﹣(x﹣40)]x=﹣x2+140x,(40<m≤100);
x>m时,y=(140﹣m)x.
所以y=f(x)=.
(ii)①当0<x≤40时,y=100x,y随x增大而增大,
②当40<m≤100时,140﹣m>0.
所以y=(140﹣m)x,y随x增大而增大.
当40<x≤m时,
y=﹣x2+140x=﹣(x﹣70)2+4900,
所以当40<x≤70时,y随x增大而增大;当x>70时,y随x增大而减小.
所以当40<x≤70时,y=﹣(x﹣70)2+4900,y随x增大而增大.
综上所述,当40<m≤70时,景点收取的总费用随着团队中人数增加而增加.
20.解:(1)因为,
所以.
(2)证明:,
因为函数y=lgx在(1,+∞)上单调递增,
函数在(1,+∞)上单调递增,
所以g(x)在(1,+∞)上单调递增,
又因为,
,
所以g(10) g(100)<0,
所以 x0∈(10,100),g(x0)=0,即g(x)在(1,+∞)上有且仅有一个零点.
21.解:(1)f(x)是定义域为R的奇函数,则f(0)=0,
∴k=1,f(x)在R上单调递增,
任取x1<x2,
则f(x1)﹣f(x2)=﹣﹣+
=()(1+)
由于a>1,x1<x2,
则,,
得f(x1)﹣f(x2)<0,f(x)在R上单调递增,得证;
(2),得a=2,
g(x)=a2x+a﹣2x﹣f(x)=22x+2﹣2x﹣(2x﹣2﹣x)=(2x﹣2﹣x)2﹣(2x﹣2﹣x)+2,
令t=f(x)=2x﹣2﹣x,由(1)知f(x)为增函数,x∈[﹣1,1],,
设,
当t=时,函数取得最小值,当t=﹣时,函数取得最大值,
故函数的值域为.
22解:(1)当0<a<1时,不等式f(7﹣2a)≤f(5a) ,
解得0<a<1;
当a>1时,不等式f(7﹣2a)≤f(5a) ,
解得1<a<.
综上所述,不等式的解集为(0,1)∪(1,).
(2)存在k>2使f(4x+3)﹣f(k 2x+1)<0在[0,1]上恒成立.
因为m2+1>0,所以
,
当且仅当,即m=0时取等号,
又由恒成立,可知f(x)为增函数,所以a>1,
f(4x+3)﹣f(k 2x+1)<0在x∈[0,1]时恒成立,
即f(4x+3)<f(k 2x+1)在x∈[0,1]时恒成立,
即4x+3<k 2x+1在x∈[0,1]时恒成立,
即=在x∈[0,1]时恒成立,
令t=2x,因为x∈[0,1],所以t∈[1,2],
g(t)=在[1,]上单调递减,在[,2]上单调递增,
且g(1)=2,g(2)=,
所以g(t)在[1,2]上的最大值为2,
即的最大值为2,所以存在k>2使f(4x+3)﹣f(k 2x+1)<0在[0,1]上恒成立.
所以k的取值范围是[2,+∞).
同课章节目录
