函数的奇偶性课件
图片预览



文档简介
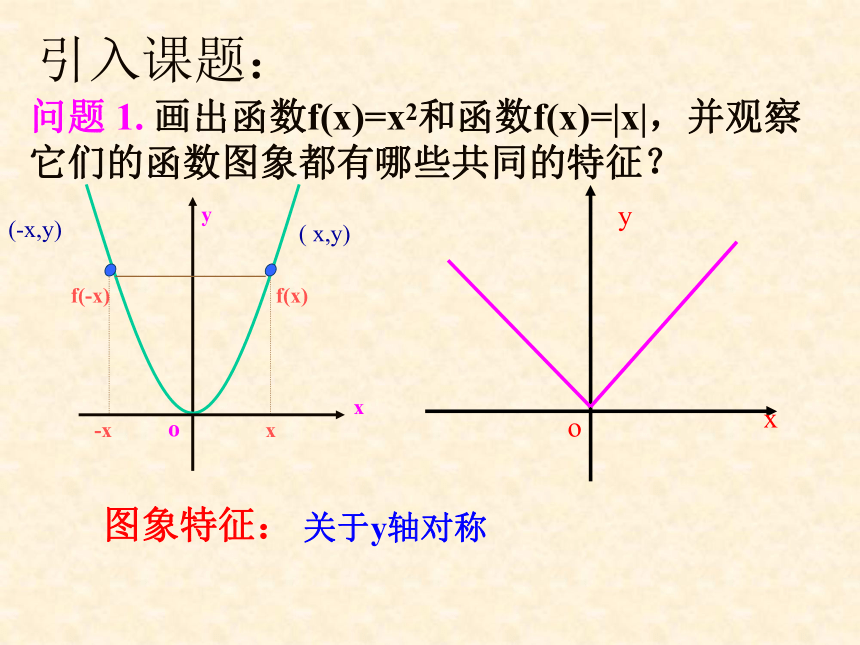
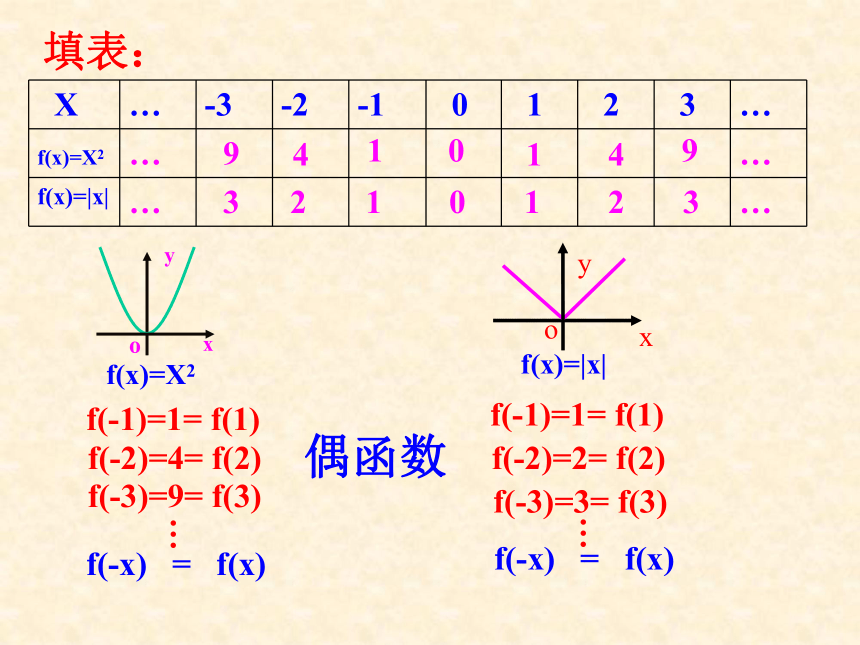
课件17张PPT。引入课题:问题 1. 画出函数f(x)=x2和函数f(x)=|x|,并观察它们的函数图象都有哪些共同的特征?图象特征:关于y轴对称填表:f(-1)=1= f(1)f(-2)=4= f(2)…f(-x) = f(x) f(-3)=9= f(3)偶函数941
0
14 93 2 1 0 1 2 3思考:如何用数学语言来描述偶函数的定义?偶函数:
如果对于f(x)定义域内的任意一个x,
都有 f(-x)=f(x),
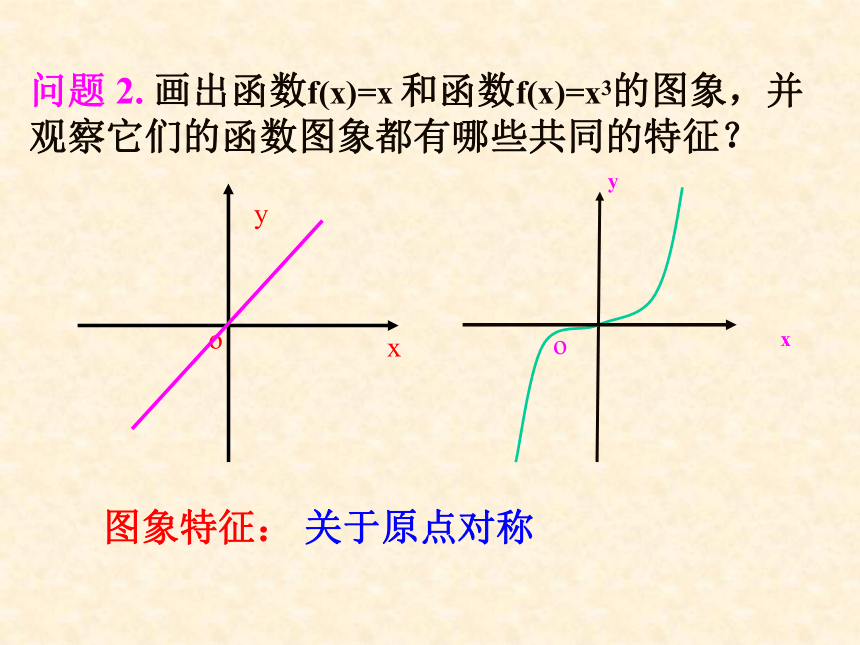
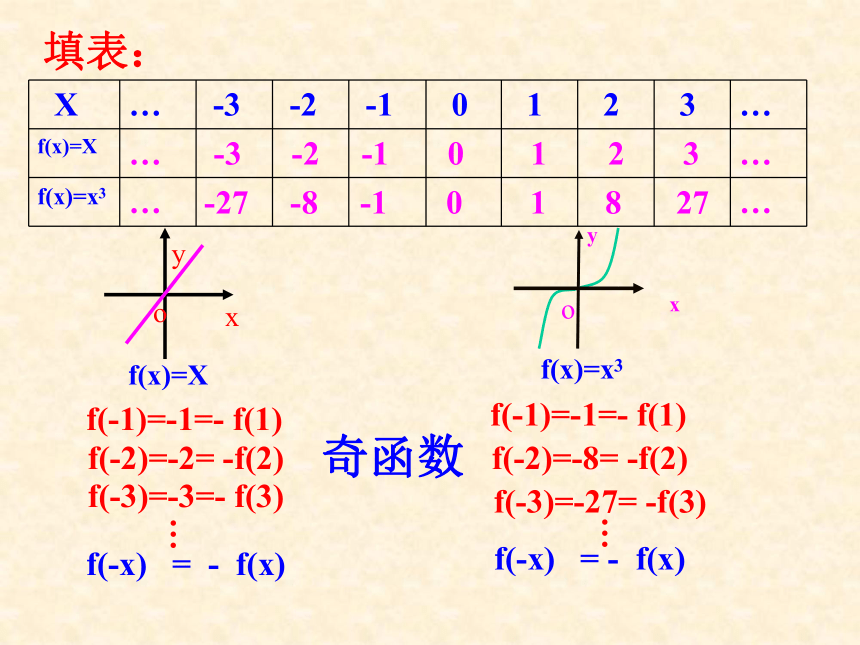
那么函数f(x)就叫偶函数.问题 2. 画出函数f(x)=x 和函数f(x)=x3的图象,并观察它们的函数图象都有哪些共同的特征?图象特征: 关于原点对称填表:f(-1)=-1=- f(1)f(-2)=-2= -f(2)…f(-x) = - f(x) f(-3)=-3=- f(3)奇函数-3 -2 -1 0 1 2 3-27 -8 -1 0 1 8 27对照偶函数的定义说出奇函数的定义?奇函数:
如果对于f(x)定义域内的任意一个x,
都有 f(-x)=-f(x),
那么函数f(x)就叫奇函数.思考:我把f(x)=x2的图象擦去一部分,把f(x)=|x|的定义域加个条件(x≠1),他们还是不是偶函数呢?图象不关于y轴对称,所以不是偶函数。说明判断函数奇偶性首先要看定义域是否关于原点对称判断函数的奇偶性:
方法一:(1)定义域是否关于原点对称;
(2)看f(x)与±f(x)是否相等;
(3)根据定义下结论。
方法二:图象的各有属性例1 判断下列函数的奇偶性(2) f(x)= - x2 +1∴f(x)为奇函数 ∵f(-x)= -(-x)2+1
= - x2+1∴f(x)为偶函数解:定义域为﹛x|x≠0﹜解:定义域为R= - f(x) = f(x)(3) f(x)=x2+x解:定义域为R
f(-x)=(-x)2 +(-x)=x2-x∴f(x)为非奇非偶函数f(-x)≠f(x) ,f(-x)≠-f(x)
(1)看定义域是否关于原点对称,
若不对称必为非奇非偶 ;
(2)若定义域对称,则看是否满足f(x)=f(-x)或f(x)=-f(-x),若均不
满足为非奇非偶函数 .
如何判断非奇非偶函数? 思考:函数按奇偶性的分类可分为哪几类?(1)奇函数(2)偶函数(3)非奇非偶函数那存不存在既是奇函数又是偶函数的函数呢?问 :既是奇函数又是偶函数的函数有多少?无数个函数按奇偶性的分类可分为四类:(1)奇函数(2)偶函数(3)非奇非偶函数(4)既奇又偶函数例2 判断函数 f(x)=m (m为常数) 的奇偶性解(1)当m=0时,f(x)=0 f(x)既是奇函数又是偶函数(2)当m≠0时,f(x)=m, f(x)是偶函数课后思考题(能力拓展)若函数f(x)=(m-1)x2+2mx+3是偶函数,求m的值☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,
那么这个函数为奇函数.⑵ 偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.注:奇偶函数图象的性质可用于:
①.判断函数的奇偶性。
②.简化函数图象的画法。作业:课后练习题 2请同学们做好课后复习!谢谢评委老师观看指导!
0
14 93 2 1 0 1 2 3思考:如何用数学语言来描述偶函数的定义?偶函数:
如果对于f(x)定义域内的任意一个x,
都有 f(-x)=f(x),
那么函数f(x)就叫偶函数.问题 2. 画出函数f(x)=x 和函数f(x)=x3的图象,并观察它们的函数图象都有哪些共同的特征?图象特征: 关于原点对称填表:f(-1)=-1=- f(1)f(-2)=-2= -f(2)…f(-x) = - f(x) f(-3)=-3=- f(3)奇函数-3 -2 -1 0 1 2 3-27 -8 -1 0 1 8 27对照偶函数的定义说出奇函数的定义?奇函数:
如果对于f(x)定义域内的任意一个x,
都有 f(-x)=-f(x),
那么函数f(x)就叫奇函数.思考:我把f(x)=x2的图象擦去一部分,把f(x)=|x|的定义域加个条件(x≠1),他们还是不是偶函数呢?图象不关于y轴对称,所以不是偶函数。说明判断函数奇偶性首先要看定义域是否关于原点对称判断函数的奇偶性:
方法一:(1)定义域是否关于原点对称;
(2)看f(x)与±f(x)是否相等;
(3)根据定义下结论。
方法二:图象的各有属性例1 判断下列函数的奇偶性(2) f(x)= - x2 +1∴f(x)为奇函数 ∵f(-x)= -(-x)2+1
= - x2+1∴f(x)为偶函数解:定义域为﹛x|x≠0﹜解:定义域为R= - f(x) = f(x)(3) f(x)=x2+x解:定义域为R
f(-x)=(-x)2 +(-x)=x2-x∴f(x)为非奇非偶函数f(-x)≠f(x) ,f(-x)≠-f(x)
(1)看定义域是否关于原点对称,
若不对称必为非奇非偶 ;
(2)若定义域对称,则看是否满足f(x)=f(-x)或f(x)=-f(-x),若均不
满足为非奇非偶函数 .
如何判断非奇非偶函数? 思考:函数按奇偶性的分类可分为哪几类?(1)奇函数(2)偶函数(3)非奇非偶函数那存不存在既是奇函数又是偶函数的函数呢?问 :既是奇函数又是偶函数的函数有多少?无数个函数按奇偶性的分类可分为四类:(1)奇函数(2)偶函数(3)非奇非偶函数(4)既奇又偶函数例2 判断函数 f(x)=m (m为常数) 的奇偶性解(1)当m=0时,f(x)=0 f(x)既是奇函数又是偶函数(2)当m≠0时,f(x)=m, f(x)是偶函数课后思考题(能力拓展)若函数f(x)=(m-1)x2+2mx+3是偶函数,求m的值☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,
那么这个函数为奇函数.⑵ 偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.注:奇偶函数图象的性质可用于:
①.判断函数的奇偶性。
②.简化函数图象的画法。作业:课后练习题 2请同学们做好课后复习!谢谢评委老师观看指导!
