2015年中考数学易错题赏析:(九)选择题之压轴题
文档属性
| 名称 | 2015年中考数学易错题赏析:(九)选择题之压轴题 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-18 07:58:28 | ||
图片预览


文档简介
(九)选择题之压轴题
题型特点
选择题中的压轴题和一般选择题相比,具有综合性较强、数形兼备、解题方法多样化、充满思辨性等特点,要求学生综合运用多种知识解题,思维要有一定的广度和深度,并会运用多种不同的方法灵活解题.这类题目重点考察学生综合分析问题、解决问题的能力.
解题方法
解答这类题目的方法除常用的直选法、观察法外,重点要掌握排除法和代入法.根据题目条件从四个选项中逐次排除选项的方法,包括分析排除法和反例排除法两种.若用一般方法不能求解时,可采用代入法,就是根据题目的有关条件,采用某些特殊情况分析问题,或采用某些特殊值代入计算分析,或将题目中不易求解的字母用符合条件的某些具体的数字代入,化一般为特殊来分析问题,通常包括已知代入法、选项代入法和特殊值代入法等.特别注意:这些方法在通常都是要综合灵活运用,不能生搬硬套.www.21-cn-jy.com
易错题赏析
易错题1:如图,已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是………………………………………………( )
答案:A
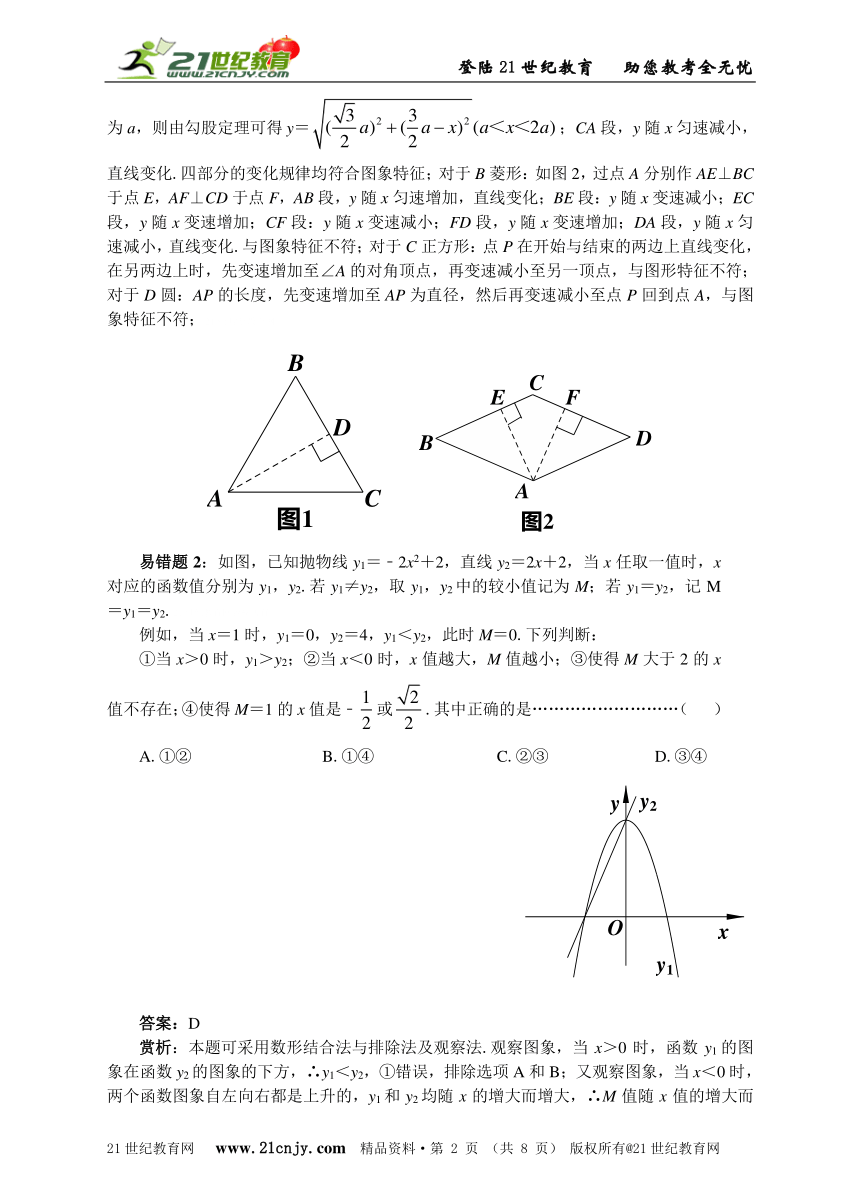
赏析:本题可采用运动过程展示与观察相结合的方法,对四个选项一一分析.对于A等边三角形:如图1,过点A作AD⊥BC于点D,AB段,y随x匀速增加,直线变化;BD段,y随x变速减小,DC段,y随x变速增加(也可:在点A的对边上时,设等边三角形的边长为a,则由勾股定理可得y=;CA段,y随x匀速减小,直线变化.四部分的变化规律均符合图象特征;对于B菱形:如图2,过点A分别作AE⊥BC于点E,AF⊥CD于点F,AB段,y随x匀速增加,直线变化;BE段:y随x变速减小;EC段,y随x变速增加;CF段:y随x变速减小;FD段,y随x变速增加;DA段,y随x匀速减小,直线变化.与图象特征不符;对于C正方形:点P在开始与结束的两边上直线变化,在另两边上时,先变速增加至∠A的对角顶点,再变速减小至另一顶点,与图形特征不符;对于D圆:AP的长度,先变速增加至AP为直径,然后再变速减小至点P回到点A,与图象特征不符;21·世纪*教育网
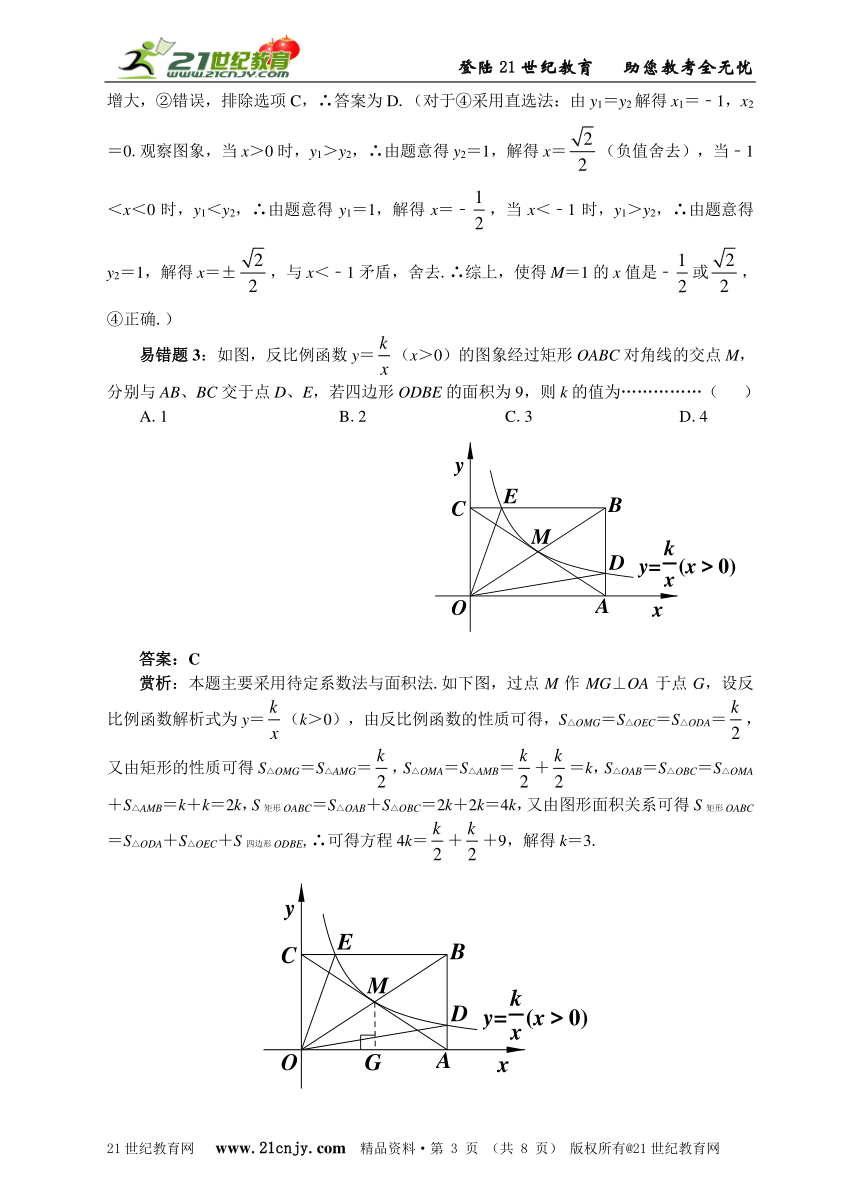
易错题2:如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.21世纪教育网版权所有
例如,当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是﹣或.其中正确的是………………………( )
A.①② B.①④ C.②③ D.③④
答案:D
赏析:本题可采用数形结合法与排除法及观察法.观察图象,当x>0时,函数y1的图象在函数y2的图象的下方,∴y1<y2,①错误,排除选项A和B;又观察图象,当x<0时,两个函数图象自左向右都是上升的,y1和y2均随x的增大而增大,∴M值随x值的增大而增大,②错误,排除选项C,∴答案为D.(对于④采用直选法:由y1=y2解得x1=﹣1,x2=0.观察图象,当x>0时,y1>y2,∴由题意得y2=1,解得x=(负值舍去),当﹣1<x<0时,y1<y2,∴由题意得y1=1,解得x=﹣,当x<﹣1时,y1>y2,∴由题意得y2=1,解得x=±,与x<﹣1矛盾,舍去.∴综上,使得M=1的x值是﹣或,④正确.)www-2-1-cnjy-com
易错题3:如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为……………( )
A.1 B.2 C.3 D.4
答案:C
赏析:本题主要采用待定系数法与面积法.如下图,过点M作MG⊥OA于点G,设反比例函数解析式为y=(k>0),由反比例函数的性质可得,S△OMG=S△OEC=S△ODA=,又由矩形的性质可得S△OMG=S△AMG=,S△OMA=S△AMB=+=k,S△OAB=S△OBC=S△OMA+S△AMB=k+k=2k,S矩形OABC=S△OAB+S△OBC=2k+2k=4k,又由图形面积关系可得S矩形OABC=S△ODA+S△OEC+S四边形ODBE,∴可得方程4k=++9,解得k=3.
易错题4:如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE,DE与FG相交于点O.设AB=a,CG=b(a>b),下列结论:①△BCG≌△DCE;②BG⊥DE;③;④(a-b)2·S△EFO=b2·S△DGO.其中结论正确的个数是……( )
A.4 B.3 C.2 D.1
答案:A
赏析:本题是四边形与三角形的综合题,难度不是很大,根据题目条件,可采用直选法:对于①:∵四边形ABCD、CEFG都是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,在△BCG和△DCE中,∵,∴△BCG≌△DCE,∴①正确;2·1·c·n·j·y
对于②:∵△BCG≌△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BGC=90°,∴∠CDE+∠DGH=90°,∴∠DHG=90°,∴BG⊥DE,∴②正确;
对于③:∵四边形CEFG是正方形,∴GF∥CE,∴△DGO∽△DCE,∴,∴③错误;
对于④:∵DC∥EF,∴∠GDO=∠OEF,∵∠GOD=∠EOF,∴△OGD∽△OFE,∴,又∵DG=DC-CG=a-b,EF=b,∴,∴,∴(a-b)2·S△EFO=b2·S△DGO,【来源:21·世纪·教育·网】
对于④也可采用逆推法:
(a-b)2·S△EFO=b2·S△DGO △OGD∽△OFE DC∥EF,此条件由正方形CEFG可得,∴再顺推得④正确.
∴答案选B.
易错题5:如图,P为⊙O的直径BA的延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:①PD与⊙O相切;②四边形PCBD是菱形;③PO=AB;④∠PDB=120°.其中正确结论的个数为…………………( )
A.4个 B.3个 C.2个 D.1个
答案:A
赏析:本题是圆与四边形、三角形的综合题,难度不大,可采用直选法.
对于①:如下图,连接OC、OD,则OC=OD.在△PCO和△PDO中,∵,∴△PCO≌△PDO,∴∠PCO=∠PDO,又∵PC与⊙O相切,∴OC⊥PC,∴∠PCO=90°,∴∠PDO=90°,∴PD⊥OD,∴PD与⊙O相切,∴①正确;21cnjy.com
对于②:∵PC、PD为⊙O的切线,∴∠CPB=∠DPB.在△CPB和△DPB中,∵∴△CPB≌△DPB,∴CB=DB,又∵PC=PD=BC,∴PC=PD=BC=DB,∴四边形PCBD是菱形,∴②正确;2-1-c-n-j-y
对于③:如下图,连接OC,则OC⊥PC,
∵OC=OB,∴∠OCB=∠OBC,
又∵∠COP=∠OCB+∠OBC,∴∠COP=2∠OBC,
又∵CB=CP,∴∠OBC=∠CPB,∴∠COP=2∠CPB,
又∵∠COP+∠CPB=90°,∴∠CPB=30°,∴PO=2OC,又∵AB=2OC,∴PO=AB,∴③正确; 21*cnjy*com
对于④:∵ ∠CPB=∠DPB,∠CPB=30°,∴∠DPB=30°,
又∵DP=DB,∴∠DPB=∠DBP=30°,
∴∠PDB=180°―∠DPB―∠DBP=180°-30°-30°=120°,
∴④正确.
∴答案为A.
易错练
1.如图,已知直线y=﹣x+2分别与x轴、y轴交于A、B两点,与双曲线y=交于E、F 两点.若AB=2EF,则k的值是……………………………………………………………( )
A.﹣1 B.1 C. D.
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中正确结论的个数是…………………………………………………………………………………………( )
A.0 B.1 C.2 D.3
3.如图1,点E为正方形ABCD边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②0<t≤5时,y=t2;③直线NH的解析式为y=﹣t+27;④若△ABE与△QBP相似,则t=秒.其中正确的结论个数为( )21·cn·jy·com
A.4 B.3 C.2 D.1
4.如图,正方形ABCD中,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确结论的个数有( )
A.2 B.3 C.4 D.5
5.如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D在优弧BC上,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6cm;③sin∠AOB=;④四边形ABOC是菱形.其中正确结论的序号是………………………………………………………………( )
A.①③ B.①②③④ C.②③④ D.①③④
参考答案
1.D 赏析:本题主要采用待定系数法和方程模型法以及构造法.如下图,作FH⊥x轴于点H,EC⊥y轴于点C,FH与EC交于点D.由一次函数解析式可求得A点坐标为(2,0),B点坐标为(0,2),则OA=OB,∴△AOB为等腰直角三角形,∴AB=OA=2,∴EF=AB=,∴△DEF也为等腰直角三角形,∴FD=DE=EF=1.设F点坐标为(t,﹣t+2),则E点坐标为(t+1,﹣t+1),将F、E两点坐标分别代入反比例函数解析式得t(﹣t+2)=(t+1)(﹣t+1),解得t=,∴F点坐标为(,),∴把F点坐标代入反比例函数解析式得k=×=.∴答案为D.21教育网
2. D 赏析:本题主要采用数形结合的方法,将方程转化为函数模型的方法.观察图象,∵二次函数次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,∴b2-4ac>0,①正确;观察图象,∵抛物线开口方向向下,∴a<0,∵抛物线与y轴交于正半轴,∴c<0,∵抛物线对称轴在y轴右侧,∴﹣>0,∴<0,∴<0,∵a<0,∴b>0,∴abc<0,②正确;将方程ax2+bx+c-m=0转化为两个函数模型:∵关于x的一元二次方程ax2+bx+c-m=0没有实数根,∴函数y=ax2+bx+c与y=m没有交点,由图象可得,当m>2时,函数y=ax2+bx+c与y=m没有交点,,当m=2时,函数y=ax2+bx+c与y=m只有一个交点,,当m<2时,函数y=ax2+bx+c与y=m有两个交点,③正确.
∵AD∥BC,∴∠AEB=∠PBF,∴sin∠PBF=sin∠AEB=,∴PF=PBsin∠PBF=t,∴当0<t≤5时,y=BQ×PF=t×t=t2,∴②正确;对于③:观察图2,把点N(7,10)代入直线NH的解析式y=﹣t+27得y=≠10,∴③不正确;对于④:观察图2得,当t=>7秒时,点P在CD上,点Q已到点C并停止运动,此时,PD=-BE-ED=-5-2=,PQ=CD-PD=4-=,∵,,∴,又∵∠A=∠Q=90°,∴△ABE∽△QBP,∴④正确.∴答案为B.
4.C 赏析:对于①:∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG(HL),∴①正确;对于②:∵EF=DE=CD=2,设BG=FG=x,则CG=6-x,在Rt△ECG中,(6-x)2+42=(x+2)2,解得x=3,∴BG=3=6-3=GC,∴②正确;对于③:∵CG=BG,BG=GF,∴GC=GF,∴△FGC是等腰三角形,∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF,∴③正确;对于④:∵S△GCB=GC·CF=×3×4=6,S△AFE=AF·EF=×6×2=6,∴S△GCB=S△AFE,∴④正确;对于⑤:∵∠BAG=∠FAG,∠DAE=∠FAE,又∵∠BAD=90°,∴∠GAF=45°,∴∠AGB+∠AED=180°-∠GAF=135°,∴⑤错误.
5.B 赏析:∵点A是劣弧BC的中点,OA为半径,∴BC⊥OA,①正确,又AC=AB,∴∠COA=∠BOA,∵∠D= 30°,∴∠COA=∠BOA=60°,∴sin∠AOB=sin60°=,∴③正确,设OA与BC交于点E,如下图,则CE=BE,在Rt△OCE中,CE=OCsin∠COE=6×=3,∴BC=2CE=6,∴②正确,又∵OC=OA=OB,∴△OAC、△OAB均为等边三角形,∴OC=CA=AB=BO,∴四边形ABOC是菱形,∴④正确.
题型特点
选择题中的压轴题和一般选择题相比,具有综合性较强、数形兼备、解题方法多样化、充满思辨性等特点,要求学生综合运用多种知识解题,思维要有一定的广度和深度,并会运用多种不同的方法灵活解题.这类题目重点考察学生综合分析问题、解决问题的能力.
解题方法
解答这类题目的方法除常用的直选法、观察法外,重点要掌握排除法和代入法.根据题目条件从四个选项中逐次排除选项的方法,包括分析排除法和反例排除法两种.若用一般方法不能求解时,可采用代入法,就是根据题目的有关条件,采用某些特殊情况分析问题,或采用某些特殊值代入计算分析,或将题目中不易求解的字母用符合条件的某些具体的数字代入,化一般为特殊来分析问题,通常包括已知代入法、选项代入法和特殊值代入法等.特别注意:这些方法在通常都是要综合灵活运用,不能生搬硬套.www.21-cn-jy.com
易错题赏析
易错题1:如图,已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是………………………………………………( )
答案:A
赏析:本题可采用运动过程展示与观察相结合的方法,对四个选项一一分析.对于A等边三角形:如图1,过点A作AD⊥BC于点D,AB段,y随x匀速增加,直线变化;BD段,y随x变速减小,DC段,y随x变速增加(也可:在点A的对边上时,设等边三角形的边长为a,则由勾股定理可得y=;CA段,y随x匀速减小,直线变化.四部分的变化规律均符合图象特征;对于B菱形:如图2,过点A分别作AE⊥BC于点E,AF⊥CD于点F,AB段,y随x匀速增加,直线变化;BE段:y随x变速减小;EC段,y随x变速增加;CF段:y随x变速减小;FD段,y随x变速增加;DA段,y随x匀速减小,直线变化.与图象特征不符;对于C正方形:点P在开始与结束的两边上直线变化,在另两边上时,先变速增加至∠A的对角顶点,再变速减小至另一顶点,与图形特征不符;对于D圆:AP的长度,先变速增加至AP为直径,然后再变速减小至点P回到点A,与图象特征不符;21·世纪*教育网
易错题2:如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.21世纪教育网版权所有
例如,当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是﹣或.其中正确的是………………………( )
A.①② B.①④ C.②③ D.③④
答案:D
赏析:本题可采用数形结合法与排除法及观察法.观察图象,当x>0时,函数y1的图象在函数y2的图象的下方,∴y1<y2,①错误,排除选项A和B;又观察图象,当x<0时,两个函数图象自左向右都是上升的,y1和y2均随x的增大而增大,∴M值随x值的增大而增大,②错误,排除选项C,∴答案为D.(对于④采用直选法:由y1=y2解得x1=﹣1,x2=0.观察图象,当x>0时,y1>y2,∴由题意得y2=1,解得x=(负值舍去),当﹣1<x<0时,y1<y2,∴由题意得y1=1,解得x=﹣,当x<﹣1时,y1>y2,∴由题意得y2=1,解得x=±,与x<﹣1矛盾,舍去.∴综上,使得M=1的x值是﹣或,④正确.)www-2-1-cnjy-com
易错题3:如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为……………( )
A.1 B.2 C.3 D.4
答案:C
赏析:本题主要采用待定系数法与面积法.如下图,过点M作MG⊥OA于点G,设反比例函数解析式为y=(k>0),由反比例函数的性质可得,S△OMG=S△OEC=S△ODA=,又由矩形的性质可得S△OMG=S△AMG=,S△OMA=S△AMB=+=k,S△OAB=S△OBC=S△OMA+S△AMB=k+k=2k,S矩形OABC=S△OAB+S△OBC=2k+2k=4k,又由图形面积关系可得S矩形OABC=S△ODA+S△OEC+S四边形ODBE,∴可得方程4k=++9,解得k=3.
易错题4:如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE,DE与FG相交于点O.设AB=a,CG=b(a>b),下列结论:①△BCG≌△DCE;②BG⊥DE;③;④(a-b)2·S△EFO=b2·S△DGO.其中结论正确的个数是……( )
A.4 B.3 C.2 D.1
答案:A
赏析:本题是四边形与三角形的综合题,难度不是很大,根据题目条件,可采用直选法:对于①:∵四边形ABCD、CEFG都是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,在△BCG和△DCE中,∵,∴△BCG≌△DCE,∴①正确;2·1·c·n·j·y
对于②:∵△BCG≌△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BGC=90°,∴∠CDE+∠DGH=90°,∴∠DHG=90°,∴BG⊥DE,∴②正确;
对于③:∵四边形CEFG是正方形,∴GF∥CE,∴△DGO∽△DCE,∴,∴③错误;
对于④:∵DC∥EF,∴∠GDO=∠OEF,∵∠GOD=∠EOF,∴△OGD∽△OFE,∴,又∵DG=DC-CG=a-b,EF=b,∴,∴,∴(a-b)2·S△EFO=b2·S△DGO,【来源:21·世纪·教育·网】
对于④也可采用逆推法:
(a-b)2·S△EFO=b2·S△DGO △OGD∽△OFE DC∥EF,此条件由正方形CEFG可得,∴再顺推得④正确.
∴答案选B.
易错题5:如图,P为⊙O的直径BA的延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:①PD与⊙O相切;②四边形PCBD是菱形;③PO=AB;④∠PDB=120°.其中正确结论的个数为…………………( )
A.4个 B.3个 C.2个 D.1个
答案:A
赏析:本题是圆与四边形、三角形的综合题,难度不大,可采用直选法.
对于①:如下图,连接OC、OD,则OC=OD.在△PCO和△PDO中,∵,∴△PCO≌△PDO,∴∠PCO=∠PDO,又∵PC与⊙O相切,∴OC⊥PC,∴∠PCO=90°,∴∠PDO=90°,∴PD⊥OD,∴PD与⊙O相切,∴①正确;21cnjy.com
对于②:∵PC、PD为⊙O的切线,∴∠CPB=∠DPB.在△CPB和△DPB中,∵∴△CPB≌△DPB,∴CB=DB,又∵PC=PD=BC,∴PC=PD=BC=DB,∴四边形PCBD是菱形,∴②正确;2-1-c-n-j-y
对于③:如下图,连接OC,则OC⊥PC,
∵OC=OB,∴∠OCB=∠OBC,
又∵∠COP=∠OCB+∠OBC,∴∠COP=2∠OBC,
又∵CB=CP,∴∠OBC=∠CPB,∴∠COP=2∠CPB,
又∵∠COP+∠CPB=90°,∴∠CPB=30°,∴PO=2OC,又∵AB=2OC,∴PO=AB,∴③正确; 21*cnjy*com
对于④:∵ ∠CPB=∠DPB,∠CPB=30°,∴∠DPB=30°,
又∵DP=DB,∴∠DPB=∠DBP=30°,
∴∠PDB=180°―∠DPB―∠DBP=180°-30°-30°=120°,
∴④正确.
∴答案为A.
易错练
1.如图,已知直线y=﹣x+2分别与x轴、y轴交于A、B两点,与双曲线y=交于E、F 两点.若AB=2EF,则k的值是……………………………………………………………( )
A.﹣1 B.1 C. D.
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中正确结论的个数是…………………………………………………………………………………………( )
A.0 B.1 C.2 D.3
3.如图1,点E为正方形ABCD边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②0<t≤5时,y=t2;③直线NH的解析式为y=﹣t+27;④若△ABE与△QBP相似,则t=秒.其中正确的结论个数为( )21·cn·jy·com
A.4 B.3 C.2 D.1
4.如图,正方形ABCD中,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确结论的个数有( )
A.2 B.3 C.4 D.5
5.如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D在优弧BC上,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6cm;③sin∠AOB=;④四边形ABOC是菱形.其中正确结论的序号是………………………………………………………………( )
A.①③ B.①②③④ C.②③④ D.①③④
参考答案
1.D 赏析:本题主要采用待定系数法和方程模型法以及构造法.如下图,作FH⊥x轴于点H,EC⊥y轴于点C,FH与EC交于点D.由一次函数解析式可求得A点坐标为(2,0),B点坐标为(0,2),则OA=OB,∴△AOB为等腰直角三角形,∴AB=OA=2,∴EF=AB=,∴△DEF也为等腰直角三角形,∴FD=DE=EF=1.设F点坐标为(t,﹣t+2),则E点坐标为(t+1,﹣t+1),将F、E两点坐标分别代入反比例函数解析式得t(﹣t+2)=(t+1)(﹣t+1),解得t=,∴F点坐标为(,),∴把F点坐标代入反比例函数解析式得k=×=.∴答案为D.21教育网
2. D 赏析:本题主要采用数形结合的方法,将方程转化为函数模型的方法.观察图象,∵二次函数次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,∴b2-4ac>0,①正确;观察图象,∵抛物线开口方向向下,∴a<0,∵抛物线与y轴交于正半轴,∴c<0,∵抛物线对称轴在y轴右侧,∴﹣>0,∴<0,∴<0,∵a<0,∴b>0,∴abc<0,②正确;将方程ax2+bx+c-m=0转化为两个函数模型:∵关于x的一元二次方程ax2+bx+c-m=0没有实数根,∴函数y=ax2+bx+c与y=m没有交点,由图象可得,当m>2时,函数y=ax2+bx+c与y=m没有交点,,当m=2时,函数y=ax2+bx+c与y=m只有一个交点,,当m<2时,函数y=ax2+bx+c与y=m有两个交点,③正确.
∵AD∥BC,∴∠AEB=∠PBF,∴sin∠PBF=sin∠AEB=,∴PF=PBsin∠PBF=t,∴当0<t≤5时,y=BQ×PF=t×t=t2,∴②正确;对于③:观察图2,把点N(7,10)代入直线NH的解析式y=﹣t+27得y=≠10,∴③不正确;对于④:观察图2得,当t=>7秒时,点P在CD上,点Q已到点C并停止运动,此时,PD=-BE-ED=-5-2=,PQ=CD-PD=4-=,∵,,∴,又∵∠A=∠Q=90°,∴△ABE∽△QBP,∴④正确.∴答案为B.
4.C 赏析:对于①:∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG(HL),∴①正确;对于②:∵EF=DE=CD=2,设BG=FG=x,则CG=6-x,在Rt△ECG中,(6-x)2+42=(x+2)2,解得x=3,∴BG=3=6-3=GC,∴②正确;对于③:∵CG=BG,BG=GF,∴GC=GF,∴△FGC是等腰三角形,∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF,∴③正确;对于④:∵S△GCB=GC·CF=×3×4=6,S△AFE=AF·EF=×6×2=6,∴S△GCB=S△AFE,∴④正确;对于⑤:∵∠BAG=∠FAG,∠DAE=∠FAE,又∵∠BAD=90°,∴∠GAF=45°,∴∠AGB+∠AED=180°-∠GAF=135°,∴⑤错误.
5.B 赏析:∵点A是劣弧BC的中点,OA为半径,∴BC⊥OA,①正确,又AC=AB,∴∠COA=∠BOA,∵∠D= 30°,∴∠COA=∠BOA=60°,∴sin∠AOB=sin60°=,∴③正确,设OA与BC交于点E,如下图,则CE=BE,在Rt△OCE中,CE=OCsin∠COE=6×=3,∴BC=2CE=6,∴②正确,又∵OC=OA=OB,∴△OAC、△OAB均为等边三角形,∴OC=CA=AB=BO,∴四边形ABOC是菱形,∴④正确.
同课章节目录
