14.2三角形的内角和
图片预览




文档简介
课件12张PPT。数学中的一些美丽定理具有这样的特性:
它们极易从事实中归纳出来,?
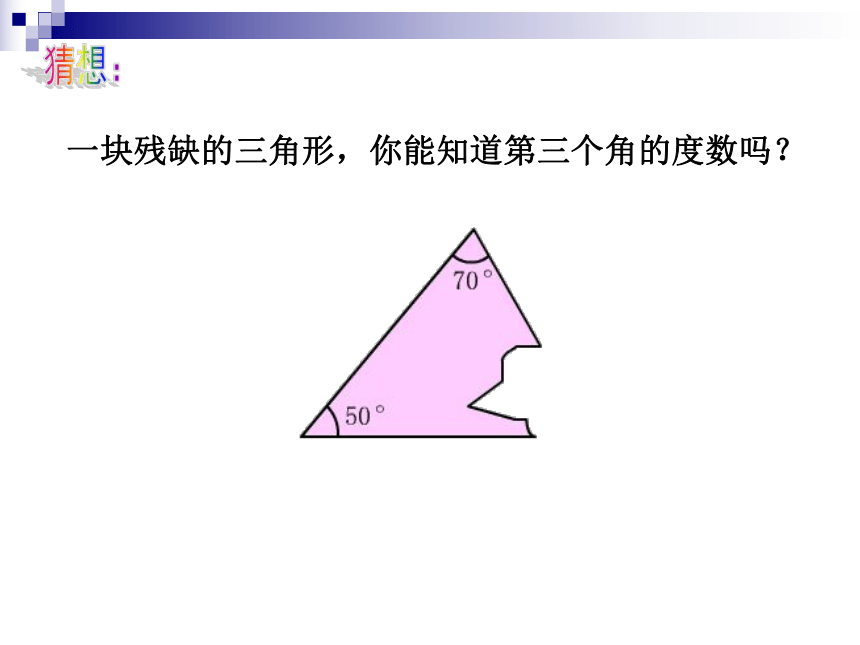
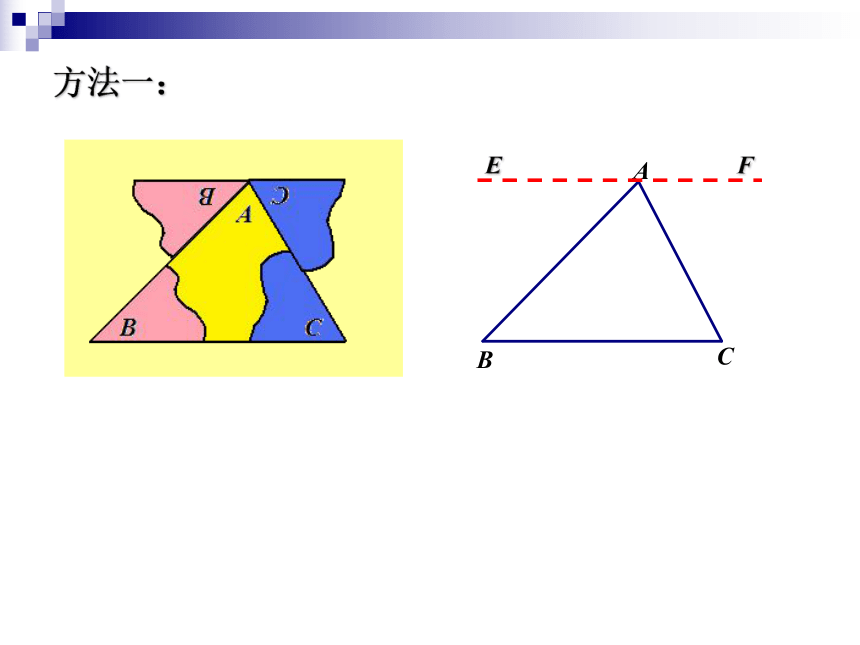
但证明却隐藏起来了. . . . . . 一块残缺的三角形,你能知道第三个角的度数吗?猜想:14.2 三角形的内角和方法一:方法二:三角形的内角和性质:
三角形的内角和等于180° 结论:三角形的内角和等于180° 例1:在△ABC中,已知∠B=35°,∠C=55°,
求∠A的度数,并判断△ABC的类型. 练习:如图,在△ABC中,
∠BAC = 60°,∠C = 45°,
AD 是 ∠BAC的角平分线,
求:∠ADC 的度数.
如图,已知AB∥CD,∠B=30°,∠COD=100°,
求∠D的度数. 你很棒的,加油吧! 例2:
在 △ABC 中,已知∠A : ∠B : ∠C = 1 : 2 : 3,
求∠A、∠B、∠C 的度数. 小结说一说,这节课你学到了什么……如图,已知∠A= 85°, ∠B = 40°, ∠D = 30°,
求∠C 的度数.挑战自我:挑战自我:如图,BE、CF是△ABC的两条角平分线,
(1)若∠A=80°,∠ABC=60°,你能求出∠EGF的度数吗?
(2)若∠A=80°,你还能求出∠EGF的度数吗?
它们极易从事实中归纳出来,?
但证明却隐藏起来了. . . . . . 一块残缺的三角形,你能知道第三个角的度数吗?猜想:14.2 三角形的内角和方法一:方法二:三角形的内角和性质:
三角形的内角和等于180° 结论:三角形的内角和等于180° 例1:在△ABC中,已知∠B=35°,∠C=55°,
求∠A的度数,并判断△ABC的类型. 练习:如图,在△ABC中,
∠BAC = 60°,∠C = 45°,
AD 是 ∠BAC的角平分线,
求:∠ADC 的度数.
如图,已知AB∥CD,∠B=30°,∠COD=100°,
求∠D的度数. 你很棒的,加油吧! 例2:
在 △ABC 中,已知∠A : ∠B : ∠C = 1 : 2 : 3,
求∠A、∠B、∠C 的度数. 小结说一说,这节课你学到了什么……如图,已知∠A= 85°, ∠B = 40°, ∠D = 30°,
求∠C 的度数.挑战自我:挑战自我:如图,BE、CF是△ABC的两条角平分线,
(1)若∠A=80°,∠ABC=60°,你能求出∠EGF的度数吗?
(2)若∠A=80°,你还能求出∠EGF的度数吗?
