5.6 几何证明举例 第1课时 课件(共14张PPT) 青岛版八年级上册数学
文档属性
| 名称 | 5.6 几何证明举例 第1课时 课件(共14张PPT) 青岛版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 21:03:35 | ||
图片预览



文档简介
(共14张PPT)
第五章 几何证明初步
5.6 几何证明举例
第1课时
1.证明角角边定理;
2.根据判定两个三角形是否全等,进而推证有关线段或角相等.
思考:在前面学过的全等三角形的四个判定方法中,判定1,2,4都已经作为基本事实.你有办法证明判定方法3吗?
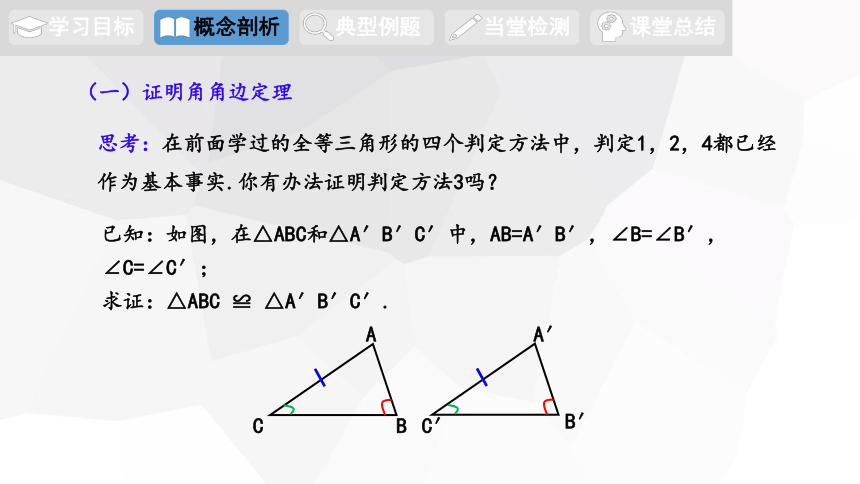
已知:如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,∠C=∠C′;
求证:△ABC ≌ △A′B′C′.
(一)证明角角边定理
A
B
C
A′
B′
C′
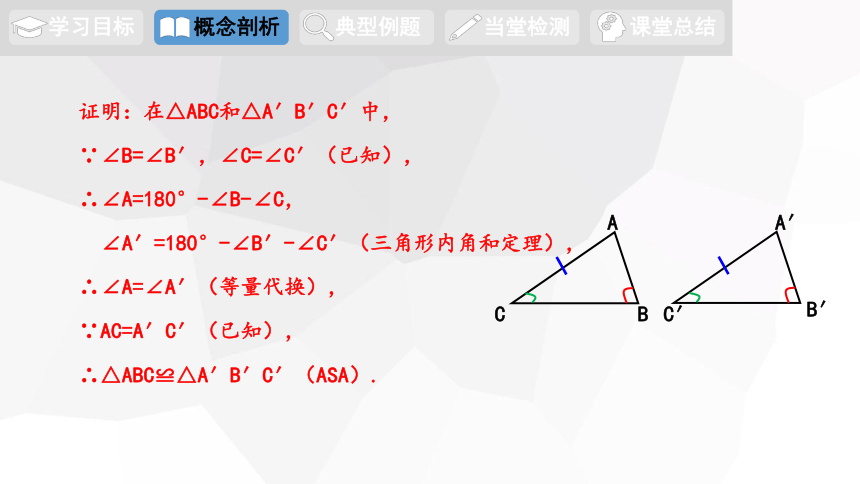
证明:在△ABC和△A′B′C′中,
∵∠B=∠B′,∠C=∠C′(已知),
∴∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′(三角形内角和定理),
∴∠A=∠A′(等量代换),
∵AC=A′C′(已知),
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
这样,全等三角形的判定就有了基本事实SAS,ASA,SSS以及定理AAS,利用它们和全等三角形的对应边、对应角相等就可以进一步推证全等三角形的有关线段或角相等.
两角分别相等且其中一组等角的对边相等的两个三角形全等.
今后,我们把全等三角形的判定方法3作为全等三角形的判定定理,即:
思考:在前面学过的全等三角形的对应角及对应边相等,那么两个全等三角形的对应边上的高线、对应边上的中线、对应角的平分线有什么性质呢?
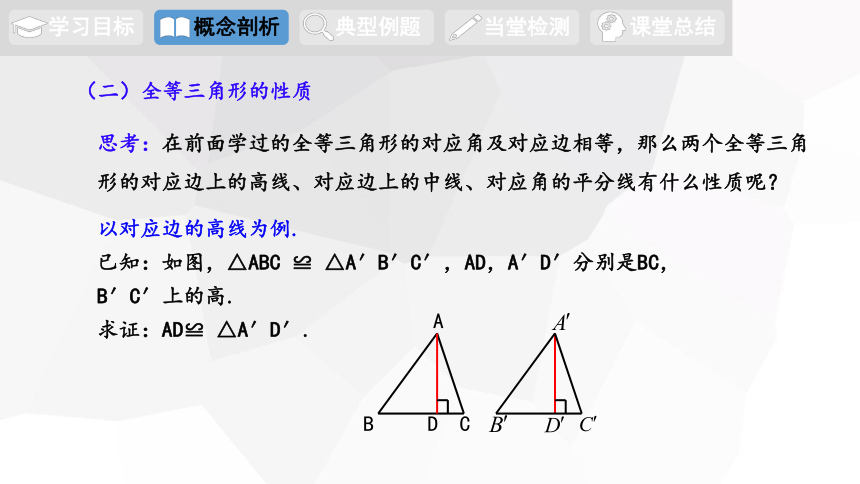
以对应边的高线为例.
已知:如图,△ABC ≌ △A′B′C′,AD,A′D′分别是BC,B′C′上的高.
求证:AD≌ △A′D′.
(二)全等三角形的性质
A
B
D
C
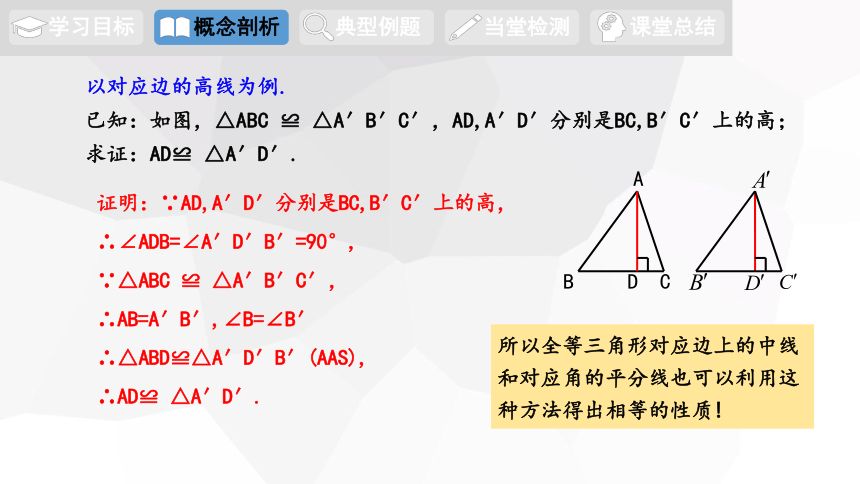
以对应边的高线为例.
已知:如图,△ABC ≌ △A′B′C′,AD,A′D′分别是BC,B′C′上的高;
求证:AD≌ △A′D′.
A
B
D
C
证明:∵AD,A′D′分别是BC,B′C′上的高,∴∠ADB=∠A′D′B′=90°,
∵△ABC ≌ △A′B′C′,
∴AB=A′B′,∠B=∠B′
∴△ABD≌△A′D′B′(AAS),
∴AD≌ △A′D′.
所以全等三角形对应边上的中线和对应角的平分线也可以利用这种方法得出相等的性质!
归纳总结:
全等三角形对应边上的中线、对应角的角平分线、对应边上的高线相等.
例1.已知:如图,AB=AC,DB=DC.求证:∠B=∠C.
证明:连接AD,在△ABD和△ACD中,
∵AB=AC,DB=DC(已知),AD=AD(公共边),
∴△ABD≌△ACD(SSS),
∴∠B=∠C.
A
C
B
D
方法总结:
在证明角相等或者线段相等时,可考察它们是否在给出的两个全等三角形中.如果不在,可通过添加辅助线构造全等三角形.
1.如图,已知:AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:AC=ED.
C
A
B
D
E
证明:由∠ECB=70°,可得∠ACB=110°,
又∵∠D=110°,∴∠ACB=∠D,
∵AB∥DE,∴∠CAB=∠E(两直线平行,内错角相等),
在△ADE和△BCA中:∠ACB=∠D、∠CAB=∠E、AB=AE,
∴△ADE≌△BCA(AAS),
∴AC=ED .
例2.如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在点E移动的过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.
解:相等.
理由:在△ABC和△ADC中:AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS).
∴∠DAE=∠BAE.
在△ADE和△ABE中:AB=AD,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS),∴BE=DE.
2.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC. 求证:OB=OC.
证明:∵ BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,∴∠1=∠2.
在△AOD和△AOE中:∠ADC=∠AEB,∠1=∠2,OA=AO,
∴△AOD≌△AOE(AAS),∴OD=OE.
在△BOD和△COE中:∠BDO =∠CEO,OD=OE,∠BOD=∠COE,
∴△BOD≌△COE(ASA),∴OB=OC.
思考:本节课你学到什么?
1.利用基本事实SAS证明AAS.
2.全等三角形的作用:证明有关线段和角相等.全等三角形对应边上的中线、对应角的角平分线、对应边上的高线相等.
第五章 几何证明初步
5.6 几何证明举例
第1课时
1.证明角角边定理;
2.根据判定两个三角形是否全等,进而推证有关线段或角相等.
思考:在前面学过的全等三角形的四个判定方法中,判定1,2,4都已经作为基本事实.你有办法证明判定方法3吗?
已知:如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,∠C=∠C′;
求证:△ABC ≌ △A′B′C′.
(一)证明角角边定理
A
B
C
A′
B′
C′
证明:在△ABC和△A′B′C′中,
∵∠B=∠B′,∠C=∠C′(已知),
∴∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′(三角形内角和定理),
∴∠A=∠A′(等量代换),
∵AC=A′C′(已知),
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
这样,全等三角形的判定就有了基本事实SAS,ASA,SSS以及定理AAS,利用它们和全等三角形的对应边、对应角相等就可以进一步推证全等三角形的有关线段或角相等.
两角分别相等且其中一组等角的对边相等的两个三角形全等.
今后,我们把全等三角形的判定方法3作为全等三角形的判定定理,即:
思考:在前面学过的全等三角形的对应角及对应边相等,那么两个全等三角形的对应边上的高线、对应边上的中线、对应角的平分线有什么性质呢?
以对应边的高线为例.
已知:如图,△ABC ≌ △A′B′C′,AD,A′D′分别是BC,B′C′上的高.
求证:AD≌ △A′D′.
(二)全等三角形的性质
A
B
D
C
以对应边的高线为例.
已知:如图,△ABC ≌ △A′B′C′,AD,A′D′分别是BC,B′C′上的高;
求证:AD≌ △A′D′.
A
B
D
C
证明:∵AD,A′D′分别是BC,B′C′上的高,∴∠ADB=∠A′D′B′=90°,
∵△ABC ≌ △A′B′C′,
∴AB=A′B′,∠B=∠B′
∴△ABD≌△A′D′B′(AAS),
∴AD≌ △A′D′.
所以全等三角形对应边上的中线和对应角的平分线也可以利用这种方法得出相等的性质!
归纳总结:
全等三角形对应边上的中线、对应角的角平分线、对应边上的高线相等.
例1.已知:如图,AB=AC,DB=DC.求证:∠B=∠C.
证明:连接AD,在△ABD和△ACD中,
∵AB=AC,DB=DC(已知),AD=AD(公共边),
∴△ABD≌△ACD(SSS),
∴∠B=∠C.
A
C
B
D
方法总结:
在证明角相等或者线段相等时,可考察它们是否在给出的两个全等三角形中.如果不在,可通过添加辅助线构造全等三角形.
1.如图,已知:AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:AC=ED.
C
A
B
D
E
证明:由∠ECB=70°,可得∠ACB=110°,
又∵∠D=110°,∴∠ACB=∠D,
∵AB∥DE,∴∠CAB=∠E(两直线平行,内错角相等),
在△ADE和△BCA中:∠ACB=∠D、∠CAB=∠E、AB=AE,
∴△ADE≌△BCA(AAS),
∴AC=ED .
例2.如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在点E移动的过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.
解:相等.
理由:在△ABC和△ADC中:AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS).
∴∠DAE=∠BAE.
在△ADE和△ABE中:AB=AD,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS),∴BE=DE.
2.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC. 求证:OB=OC.
证明:∵ BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,∴∠1=∠2.
在△AOD和△AOE中:∠ADC=∠AEB,∠1=∠2,OA=AO,
∴△AOD≌△AOE(AAS),∴OD=OE.
在△BOD和△COE中:∠BDO =∠CEO,OD=OE,∠BOD=∠COE,
∴△BOD≌△COE(ASA),∴OB=OC.
思考:本节课你学到什么?
1.利用基本事实SAS证明AAS.
2.全等三角形的作用:证明有关线段和角相等.全等三角形对应边上的中线、对应角的角平分线、对应边上的高线相等.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
