5.6 几何证明举例 第4课时 课件(共15张PPT) 青岛版八年级数学上册
文档属性
| 名称 | 5.6 几何证明举例 第4课时 课件(共15张PPT) 青岛版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 474.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 21:08:44 | ||
图片预览




文档简介
(共15张PPT)
第4课时
第五章 几何证明初步
5.6 几何证明举例
1.证明角平分线定理及其逆定理,并用其解决几何图形中的问题;
2.理解三角形角平分线的交点到三角形三边的距离相等.
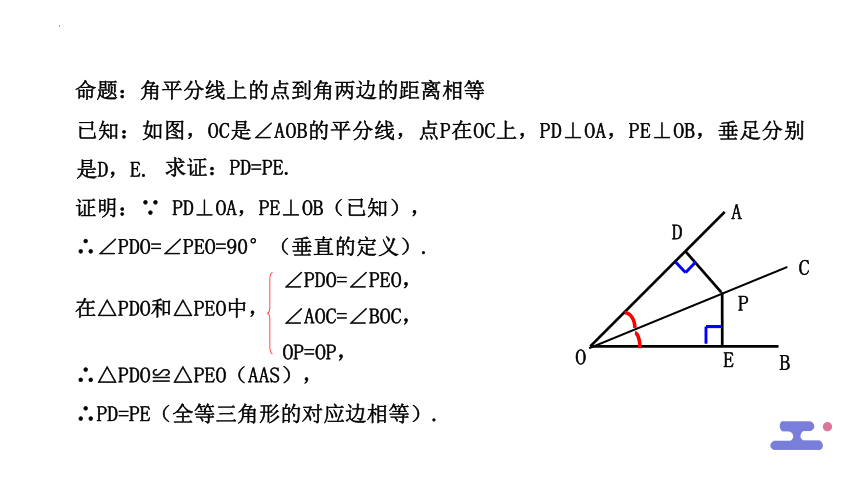
思考1:你还记得角平分线的性质什么吗?在前面我们利用什么得出了角平分线的性质吗
写出已知、求证,然后再写出具体的证明过程.
角的轴对称性质
思考2:如何证明这个性质?
角的平分线上的点到角的两边的距离相等.
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E.
证明:∵ PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义).
D
P
E
A
O
B
C
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO≌△PEO(AAS),
∴PD=PE(全等三角形的对应边相等).
命题:角平分线上的点到角两边的距离相等
在△PDO和△PEO中,
求证:PD=PE.
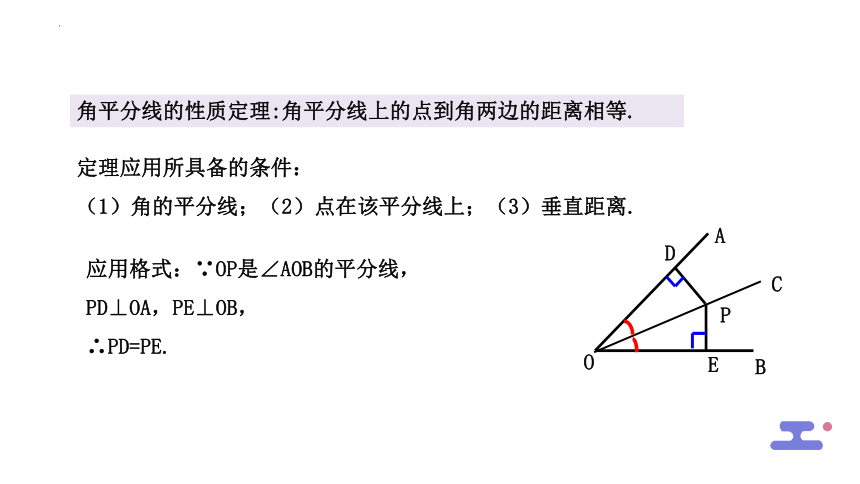
角平分线的性质定理:角平分线上的点到角两边的距离相等.
定理应用所具备的条件:
(1)角的平分线;(2)点在该平分线上;(3)垂直距离.
应用格式:∵OP是∠AOB的平分线,
PD⊥OA,PE⊥OB,
∴PD=PE.
D
P
E
A
O
B
C
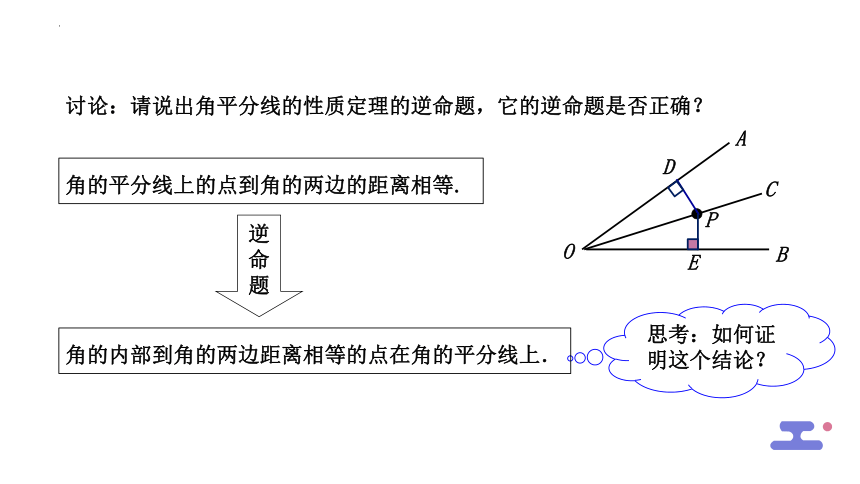
讨论:请说出角平分线的性质定理的逆命题,它的逆命题是否正确?
角的平分线上的点到角的两边的距离相等.
逆
命
题
思考:如何证明这个结论?
角的内部到角的两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
已知:如图,P是∠ABC内的一点,PM⊥AB,PN⊥BC,垂足分别是M、N,且PM=PN.求证:点P在∠AOB的角平分线上.
证明:连接MN,∵PM=PN,
∴∠PMN=∠PNM.
∵∠BMN与∠PMN互余,∠BNM与∠PNM互余,
∴∠BMN=∠BNM, ∴BM=BN.
过点B,P作射线BD.
C
A
M
B
P
N
∵BP=BP,∴△PBM≌△PBN(SSS).
∴∠ABD=∠CBD,即点P在∠AOB的角平分线上.
D
定理:角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:(1)位置关系:点在角的内部;(2)数量关系:该点到角两边的距离相等.
应用格式:∵PM⊥AB,PN⊥BC,PM=PN,
∴点P在∠AOB的平分线上.
C
A
M
B
P
N
D
例1:已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:AM平分∠DAB.
证明:过M作ME⊥AD于点E,
A
M
D
C
B
E
∵∠B=∠C=90°,
∴MC⊥DC,MB⊥AB
又∵DM平分∠ADC,
∴ME=MC(角平分线上的点到角两边的距离相等),
∵M是BC的中点,∴MC=MB, ∴ME=MB,
∴AM平分∠DAB(到角两边距离相等的点在这个角的平分线上).
1.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC、BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证:OE=OF.
证明:在△ABD和△CBD中,AB=CB,AD=CD,BD=BD
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∴BD平分∠ABC.
又∵OE⊥AB,OF⊥CB, ∴OE=OF.
例2:已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到AB、BC、CA的距离相等.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.(角平分线上的点到角两边的距离相等)
∴PD=PE=PF.(等量代换)
即点P到AB、BC、CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
D
E
F
A
B
C
P
N
M
想一想:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
解:点P在∠A的平分线上.
证明:连接AP,
由上题可得,PD=PF.
∴AP平分∠BAC.(角的内部到角两边距离相等的点在角的平分线上)
D
E
F
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
2.如图,在△ABC中,点O到三边的距离相等,∠BAC=60°,则∠BOC= .
120°
解:∵点O在△ABC内,且到三边的距离相等,
∴点O是△ABC三个内角的平分线的交点,
在△BCO中,∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
3.已知:如图,O是三条角平分线的交点,OD⊥BC,ON⊥AB,OM⊥AC,,OD=3,△ABC的周长为15,求S△ABC.
解:∵OB,OC,OA分别平分∠ABC,∠ACB和∠BAC,OD⊥BC,ON⊥AB,OM⊥AC,
∴OD=ON=OM,
∴S△ABC=S△OBC+S△OAC+S△OAB
A
B
C
O
M
N
G
D
思考:本节课你学到什么?
角平分线
性质定理
逆定理
应用:三角形内角平分线的性质
第4课时
第五章 几何证明初步
5.6 几何证明举例
1.证明角平分线定理及其逆定理,并用其解决几何图形中的问题;
2.理解三角形角平分线的交点到三角形三边的距离相等.
思考1:你还记得角平分线的性质什么吗?在前面我们利用什么得出了角平分线的性质吗
写出已知、求证,然后再写出具体的证明过程.
角的轴对称性质
思考2:如何证明这个性质?
角的平分线上的点到角的两边的距离相等.
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E.
证明:∵ PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义).
D
P
E
A
O
B
C
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO≌△PEO(AAS),
∴PD=PE(全等三角形的对应边相等).
命题:角平分线上的点到角两边的距离相等
在△PDO和△PEO中,
求证:PD=PE.
角平分线的性质定理:角平分线上的点到角两边的距离相等.
定理应用所具备的条件:
(1)角的平分线;(2)点在该平分线上;(3)垂直距离.
应用格式:∵OP是∠AOB的平分线,
PD⊥OA,PE⊥OB,
∴PD=PE.
D
P
E
A
O
B
C
讨论:请说出角平分线的性质定理的逆命题,它的逆命题是否正确?
角的平分线上的点到角的两边的距离相等.
逆
命
题
思考:如何证明这个结论?
角的内部到角的两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
已知:如图,P是∠ABC内的一点,PM⊥AB,PN⊥BC,垂足分别是M、N,且PM=PN.求证:点P在∠AOB的角平分线上.
证明:连接MN,∵PM=PN,
∴∠PMN=∠PNM.
∵∠BMN与∠PMN互余,∠BNM与∠PNM互余,
∴∠BMN=∠BNM, ∴BM=BN.
过点B,P作射线BD.
C
A
M
B
P
N
∵BP=BP,∴△PBM≌△PBN(SSS).
∴∠ABD=∠CBD,即点P在∠AOB的角平分线上.
D
定理:角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:(1)位置关系:点在角的内部;(2)数量关系:该点到角两边的距离相等.
应用格式:∵PM⊥AB,PN⊥BC,PM=PN,
∴点P在∠AOB的平分线上.
C
A
M
B
P
N
D
例1:已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:AM平分∠DAB.
证明:过M作ME⊥AD于点E,
A
M
D
C
B
E
∵∠B=∠C=90°,
∴MC⊥DC,MB⊥AB
又∵DM平分∠ADC,
∴ME=MC(角平分线上的点到角两边的距离相等),
∵M是BC的中点,∴MC=MB, ∴ME=MB,
∴AM平分∠DAB(到角两边距离相等的点在这个角的平分线上).
1.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC、BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证:OE=OF.
证明:在△ABD和△CBD中,AB=CB,AD=CD,BD=BD
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∴BD平分∠ABC.
又∵OE⊥AB,OF⊥CB, ∴OE=OF.
例2:已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到AB、BC、CA的距离相等.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.(角平分线上的点到角两边的距离相等)
∴PD=PE=PF.(等量代换)
即点P到AB、BC、CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
D
E
F
A
B
C
P
N
M
想一想:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
解:点P在∠A的平分线上.
证明:连接AP,
由上题可得,PD=PF.
∴AP平分∠BAC.(角的内部到角两边距离相等的点在角的平分线上)
D
E
F
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
2.如图,在△ABC中,点O到三边的距离相等,∠BAC=60°,则∠BOC= .
120°
解:∵点O在△ABC内,且到三边的距离相等,
∴点O是△ABC三个内角的平分线的交点,
在△BCO中,∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
3.已知:如图,O是三条角平分线的交点,OD⊥BC,ON⊥AB,OM⊥AC,,OD=3,△ABC的周长为15,求S△ABC.
解:∵OB,OC,OA分别平分∠ABC,∠ACB和∠BAC,OD⊥BC,ON⊥AB,OM⊥AC,
∴OD=ON=OM,
∴S△ABC=S△OBC+S△OAC+S△OAB
A
B
C
O
M
N
G
D
思考:本节课你学到什么?
角平分线
性质定理
逆定理
应用:三角形内角平分线的性质
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
