11.3 图形的中心对称 第2课时 课件(共16张PPT)青岛版八年级数学下册
文档属性
| 名称 | 11.3 图形的中心对称 第2课时 课件(共16张PPT)青岛版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 06:56:27 | ||
图片预览





文档简介
(共16张PPT)
第十一章 图形的平移与旋转
11.3 图形的中心对称
第2课时
1.了解中心对称图形的概念;
2.掌握线段、平行四边形(包括矩形、菱形、正方形)等平面图形的中心对称性质.
在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做中心对称图形,这个点叫做它的对称中心.
想一想:观察下面的图形,它们有何共同特征?
一个图形绕某个点旋转180°,
旋转后的图形与原图形重合.
思考:1.如图,将线段AB绕它的中点O旋转180°,你有什么发现?
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
A
B
O
因此,线段是中心对称图形,中点O是对称中心.
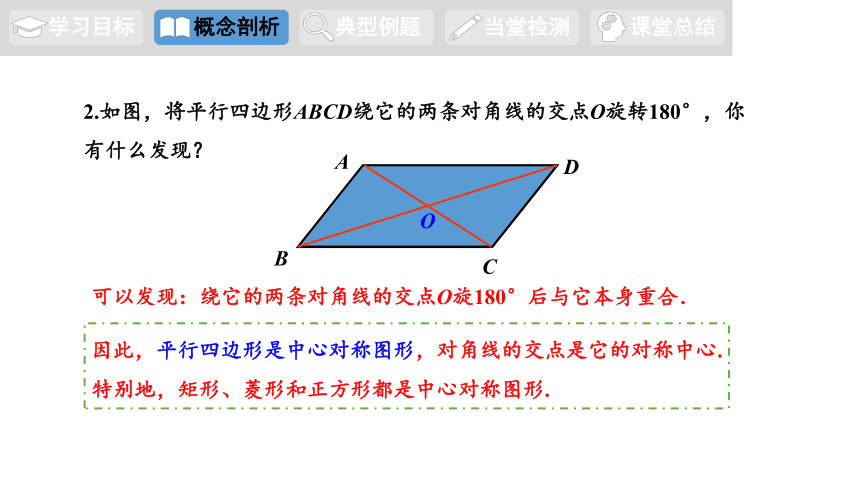
2.如图,将平行四边形ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
可以发现:绕它的两条对角线的交点O旋180°后与它本身重合.
因此,平行四边形是中心对称图形,对角线的交点是它的对称中心.
特别地,矩形、菱形和正方形都是中心对称图形.
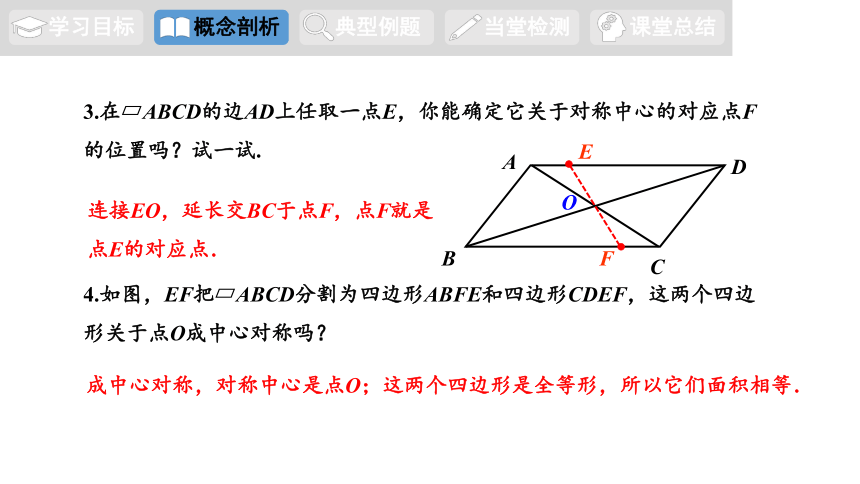
3.在 ABCD的边AD上任取一点E,你能确定它关于对称中心的对应点F的位置吗?试一试.
A
B
C
D
O
E
F
连接EO,延长交BC于点F,点F就是点E的对应点.
4.如图,EF把 ABCD分割为四边形ABFE和四边形CDEF,这两个四边形关于点O成中心对称吗?
成中心对称,对称中心是点O;这两个四边形是全等形,所以它们面积相等.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
例1.下面26个英文大写正体字母中,哪些是轴对称图形,哪些是中心对称图形?
解:26个大写英文字母中,是轴对称图形的有:
A、B、C、D、E、H、I、K、M、O、T、U、V、W、X、Y;
是中心对称图形的有:H、I、N、O、S、X、Z.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
中心对称图形与轴对称图形有什么区别和联系?
1.下图中的中心对称图形有 ,是轴对称图形的有 .
①
②
③
④
①②③⑥
⑤
⑥
⑦
③④⑥
归纳总结
轴对称图形与中心对称图形的区别和联系:
轴对称图形 中心对称图形
有对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴 垂直平分 对称点连线经过对称中心,
且被对称中心平分
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案一:正方形ABCD的两条对角线AC和BD可作为小路的位置,此时正方形被分成四个全等的等腰直角三角形.
O
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案二:正方形ABCD两组对边中点的连线EG和HF可作为小路的位置,此时正方形被分成四个全等的小正方形.
H
O
F
G
E
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案三:过正方形的对称中心O,任意作两条互相垂直的直线EG,HF,分别交AB,CD于点H,F,交BC,AD于点E,G,则EG与HF可作为小路的位置.
H
O
F
G
E
记四边形OGAH,OHBE,OECF,OFDG的面积分别为S1,S2,S3,S4.
S1
S2
S4
S3
∵GE,HF过点O,∴四边形GABE与ECDG以及HBCF与FDAH分别关于点O成中心对称.∴S1+S2=S3+S4①,S2+S3=S4+S1②.
整理可得S1=S3,S2=S4.
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
H
O
F
G
E
连接OA,OB,则OA=OB,∠AOB=90°.
∵∠AOG和∠BOH都与∠AOH互余,
∴∠AOG=∠BOH,∠GAO=∠HBO=45°.
∴S1=S△AOG+S△AOH=S△BOH+S△BOE=S2.
∴△AOG≌△BOH(ASA).同理△AOH≌△BOE.
∴S1=S2=S3=S4.
∴EG与HF将正方形ABCD分为面积相等的四部分.
2.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
解析:由于矩形是中心对称图形,所以依题意
可知△BOF与△DOE关于点O成中心对称,由
此图中阴影部分的三个三角形就可以转化到
Rt△ADC中,易得阴影部分的面积为3.
3
3.有一块如图所示的钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出分割方法.
解:钢板可看成由上、下两个矩形构成或左、右两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,
自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过这两个对称中心作直线即可.(画法不唯一)
回顾本节课,请回答问题:
1.中心对称图形是什么?
2.如何利用平行四边形的中心对称性质将平行四边形切割面积相等的四部分?
第十一章 图形的平移与旋转
11.3 图形的中心对称
第2课时
1.了解中心对称图形的概念;
2.掌握线段、平行四边形(包括矩形、菱形、正方形)等平面图形的中心对称性质.
在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做中心对称图形,这个点叫做它的对称中心.
想一想:观察下面的图形,它们有何共同特征?
一个图形绕某个点旋转180°,
旋转后的图形与原图形重合.
思考:1.如图,将线段AB绕它的中点O旋转180°,你有什么发现?
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
A
B
O
因此,线段是中心对称图形,中点O是对称中心.
2.如图,将平行四边形ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
可以发现:绕它的两条对角线的交点O旋180°后与它本身重合.
因此,平行四边形是中心对称图形,对角线的交点是它的对称中心.
特别地,矩形、菱形和正方形都是中心对称图形.
3.在 ABCD的边AD上任取一点E,你能确定它关于对称中心的对应点F的位置吗?试一试.
A
B
C
D
O
E
F
连接EO,延长交BC于点F,点F就是点E的对应点.
4.如图,EF把 ABCD分割为四边形ABFE和四边形CDEF,这两个四边形关于点O成中心对称吗?
成中心对称,对称中心是点O;这两个四边形是全等形,所以它们面积相等.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
例1.下面26个英文大写正体字母中,哪些是轴对称图形,哪些是中心对称图形?
解:26个大写英文字母中,是轴对称图形的有:
A、B、C、D、E、H、I、K、M、O、T、U、V、W、X、Y;
是中心对称图形的有:H、I、N、O、S、X、Z.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
中心对称图形与轴对称图形有什么区别和联系?
1.下图中的中心对称图形有 ,是轴对称图形的有 .
①
②
③
④
①②③⑥
⑤
⑥
⑦
③④⑥
归纳总结
轴对称图形与中心对称图形的区别和联系:
轴对称图形 中心对称图形
有对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴 垂直平分 对称点连线经过对称中心,
且被对称中心平分
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案一:正方形ABCD的两条对角线AC和BD可作为小路的位置,此时正方形被分成四个全等的等腰直角三角形.
O
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案二:正方形ABCD两组对边中点的连线EG和HF可作为小路的位置,此时正方形被分成四个全等的小正方形.
H
O
F
G
E
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
方案三:过正方形的对称中心O,任意作两条互相垂直的直线EG,HF,分别交AB,CD于点H,F,交BC,AD于点E,G,则EG与HF可作为小路的位置.
H
O
F
G
E
记四边形OGAH,OHBE,OECF,OFDG的面积分别为S1,S2,S3,S4.
S1
S2
S4
S3
∵GE,HF过点O,∴四边形GABE与ECDG以及HBCF与FDAH分别关于点O成中心对称.∴S1+S2=S3+S4①,S2+S3=S4+S1②.
整理可得S1=S3,S2=S4.
例2.如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同方案?画出图形,并说明理由.
A
B
C
D
H
O
F
G
E
连接OA,OB,则OA=OB,∠AOB=90°.
∵∠AOG和∠BOH都与∠AOH互余,
∴∠AOG=∠BOH,∠GAO=∠HBO=45°.
∴S1=S△AOG+S△AOH=S△BOH+S△BOE=S2.
∴△AOG≌△BOH(ASA).同理△AOH≌△BOE.
∴S1=S2=S3=S4.
∴EG与HF将正方形ABCD分为面积相等的四部分.
2.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
解析:由于矩形是中心对称图形,所以依题意
可知△BOF与△DOE关于点O成中心对称,由
此图中阴影部分的三个三角形就可以转化到
Rt△ADC中,易得阴影部分的面积为3.
3
3.有一块如图所示的钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出分割方法.
解:钢板可看成由上、下两个矩形构成或左、右两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,
自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过这两个对称中心作直线即可.(画法不唯一)
回顾本节课,请回答问题:
1.中心对称图形是什么?
2.如何利用平行四边形的中心对称性质将平行四边形切割面积相等的四部分?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
