11.3 图形的中心对称 第1课时 课件(共17张PPT)青岛版八年级下册数学
文档属性
| 名称 | 11.3 图形的中心对称 第1课时 课件(共17张PPT)青岛版八年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 386.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 06:59:39 | ||
图片预览




文档简介
(共17张PPT)
第十一章 图形的平移与旋转
11.3 图形的中心对称
第1课时
1.了解中心对称、两个图形成中心对称的概念;
2.掌握中心对称的基本性质,并会作和已知图形成中心对称的图形.
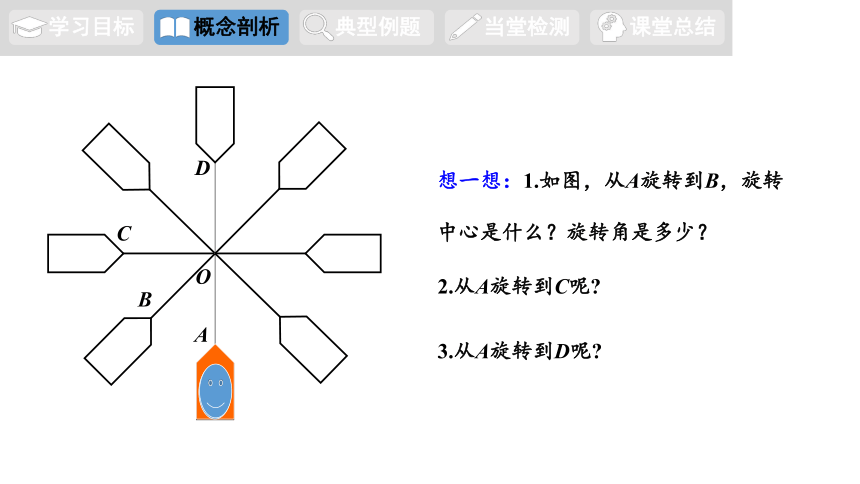
想一想:1.如图,从A旋转到B,旋转中心是什么?旋转角是多少?
O
A
B
C
D
2.从A旋转到C呢
3.从A旋转到D呢
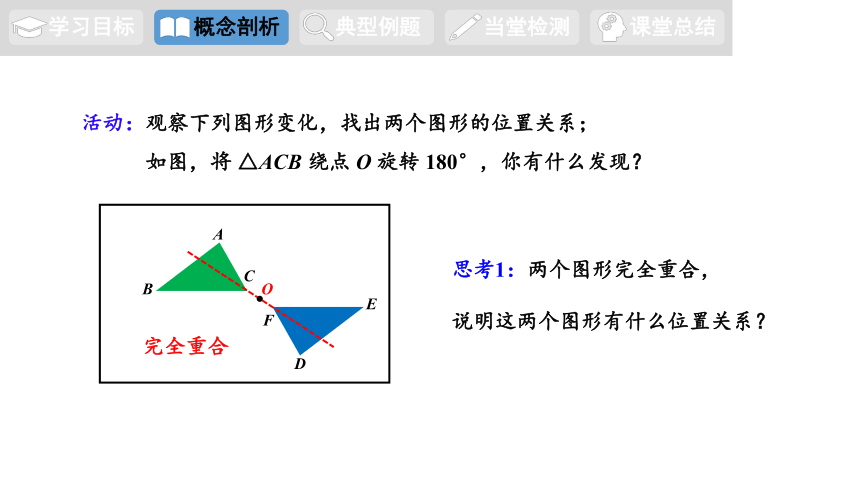
活动:观察下列图形变化,找出两个图形的位置关系;
如图,将 △ACB 绕点 O 旋转 180°,你有什么发现?
A
B
C
D
E
F
O
完全重合
思考1:两个图形完全重合,
说明这两个图形有什么位置关系?
A
B
D
E
F
O
完全重合
概念:在平面内将一个图形绕着某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,就说明这两个图形关于这个定点成中心对称.
如图,△ABC与△DEF关于点O成中心对称,点O是对称中心.点A,B,C与点D,E,F分别是对应点.
C
中心对称是旋转变化的特殊情况,成中心对称的两个图形是全等形.
A
B
D
E
F
O
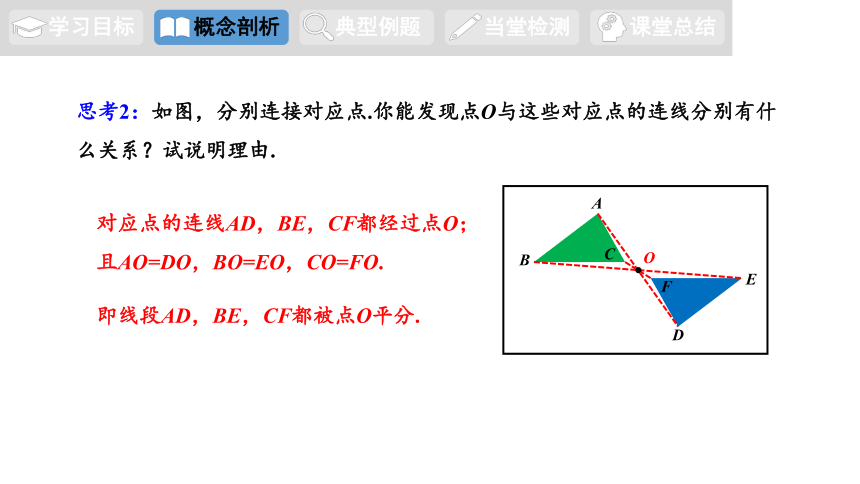
思考2:如图,分别连接对应点.你能发现点O与这些对应点的连线分别有什么关系?试说明理由.
对应点的连线AD,BE,CF都经过点O;且AO=DO,BO=EO,CO=FO.
C
即线段AD,BE,CF都被点O平分.
中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
归纳总结
例1.(1)如图,已知△ABC与△DEF 中心对称,找出它们的对称中心O.
分析:根据成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分,且被对称中心平分即可确定对称中心O.
提示:找出BE的中点O,则点O即为所求.
解:根据观察:B、E及C、F应是两组对应点;
思考:还有其他方法找出对称中心 O 吗?
A
B
C
D
E
F
O
连接BE、CF相交于点O;
则点O即为所求(如图所示).
(2)已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称(要求写出作法).
A
B
D
C
作法:
③ 顺次连接A′、B′、C′、D′各点,
四边形A′B′C′D′就是所求的四边形.
② 同样画B、C、D的对称点B′、C′、D′;
① 连接AO并延长到A′,使OA=OA′,
方法总结:作图时应结合中心对称的性质,先确定对称中心.
O
B′
A′
D′
C′
得到点A的对称点A′;
归纳总结
中心对称作图的一般步骤:(1)确定出对称中心;
(2)确定出原图形的关键点(如三角形的顶点、图形的拐点等);
(3)作出这些关键点关于对称中心的对应点;
(4)顺次连接各对应点,即可得到所要画的图形.
解:作图过程如图所示.
A
C
B
O
A′
C′
B′
1. 如图,画出与△ABC关于点O对称的△A′B′C′.
做一做:如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.A(4,0),B(0,-3),C(2,1),D(-1,2),E(-4,-3).
A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(4,3).
A′
B′
C′
D′
E′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
关于原点对称的点的坐标的规律:
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点为P′(-x,-y).
归纳总结
例2.如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
-2
2
-2
-4
4
-4
x
y
O
2
4
A
B
C
B′
A′
C′
解:△ABC的三个顶点的坐标
分别为A(-4,1),B(-1,-1),C(-3,2).
依次连接A′,B′,C′便可得到所求作的三角形.
它们关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2).
2.已知:如图,E(-4,2),F(-1,-1),以O为中心,作△EFO的关于原点中心对称图形.
解:E′的坐标为(4,-2),
F′的坐标为(1,1)
依次连接O,E′,F′,
△E′F′O为△EFO的中心对称图形.
E′
F′
3.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 .
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
①与②
①与③
回顾本节课,请回答问题:
1.什么是中心对称?
2.如何作和已知图形成中心对称的图形?
第十一章 图形的平移与旋转
11.3 图形的中心对称
第1课时
1.了解中心对称、两个图形成中心对称的概念;
2.掌握中心对称的基本性质,并会作和已知图形成中心对称的图形.
想一想:1.如图,从A旋转到B,旋转中心是什么?旋转角是多少?
O
A
B
C
D
2.从A旋转到C呢
3.从A旋转到D呢
活动:观察下列图形变化,找出两个图形的位置关系;
如图,将 △ACB 绕点 O 旋转 180°,你有什么发现?
A
B
C
D
E
F
O
完全重合
思考1:两个图形完全重合,
说明这两个图形有什么位置关系?
A
B
D
E
F
O
完全重合
概念:在平面内将一个图形绕着某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,就说明这两个图形关于这个定点成中心对称.
如图,△ABC与△DEF关于点O成中心对称,点O是对称中心.点A,B,C与点D,E,F分别是对应点.
C
中心对称是旋转变化的特殊情况,成中心对称的两个图形是全等形.
A
B
D
E
F
O
思考2:如图,分别连接对应点.你能发现点O与这些对应点的连线分别有什么关系?试说明理由.
对应点的连线AD,BE,CF都经过点O;且AO=DO,BO=EO,CO=FO.
C
即线段AD,BE,CF都被点O平分.
中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
归纳总结
例1.(1)如图,已知△ABC与△DEF 中心对称,找出它们的对称中心O.
分析:根据成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分,且被对称中心平分即可确定对称中心O.
提示:找出BE的中点O,则点O即为所求.
解:根据观察:B、E及C、F应是两组对应点;
思考:还有其他方法找出对称中心 O 吗?
A
B
C
D
E
F
O
连接BE、CF相交于点O;
则点O即为所求(如图所示).
(2)已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称(要求写出作法).
A
B
D
C
作法:
③ 顺次连接A′、B′、C′、D′各点,
四边形A′B′C′D′就是所求的四边形.
② 同样画B、C、D的对称点B′、C′、D′;
① 连接AO并延长到A′,使OA=OA′,
方法总结:作图时应结合中心对称的性质,先确定对称中心.
O
B′
A′
D′
C′
得到点A的对称点A′;
归纳总结
中心对称作图的一般步骤:(1)确定出对称中心;
(2)确定出原图形的关键点(如三角形的顶点、图形的拐点等);
(3)作出这些关键点关于对称中心的对应点;
(4)顺次连接各对应点,即可得到所要画的图形.
解:作图过程如图所示.
A
C
B
O
A′
C′
B′
1. 如图,画出与△ABC关于点O对称的△A′B′C′.
做一做:如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.A(4,0),B(0,-3),C(2,1),D(-1,2),E(-4,-3).
A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(4,3).
A′
B′
C′
D′
E′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
关于原点对称的点的坐标的规律:
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点为P′(-x,-y).
归纳总结
例2.如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
-2
2
-2
-4
4
-4
x
y
O
2
4
A
B
C
B′
A′
C′
解:△ABC的三个顶点的坐标
分别为A(-4,1),B(-1,-1),C(-3,2).
依次连接A′,B′,C′便可得到所求作的三角形.
它们关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2).
2.已知:如图,E(-4,2),F(-1,-1),以O为中心,作△EFO的关于原点中心对称图形.
解:E′的坐标为(4,-2),
F′的坐标为(1,1)
依次连接O,E′,F′,
△E′F′O为△EFO的中心对称图形.
E′
F′
3.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 .
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
①与②
①与③
回顾本节课,请回答问题:
1.什么是中心对称?
2.如何作和已知图形成中心对称的图形?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
