培优点4 带电粒子在复合场中的运动(含解析)2024年高考物理大二轮复习讲义
文档属性
| 名称 | 培优点4 带电粒子在复合场中的运动(含解析)2024年高考物理大二轮复习讲义 | 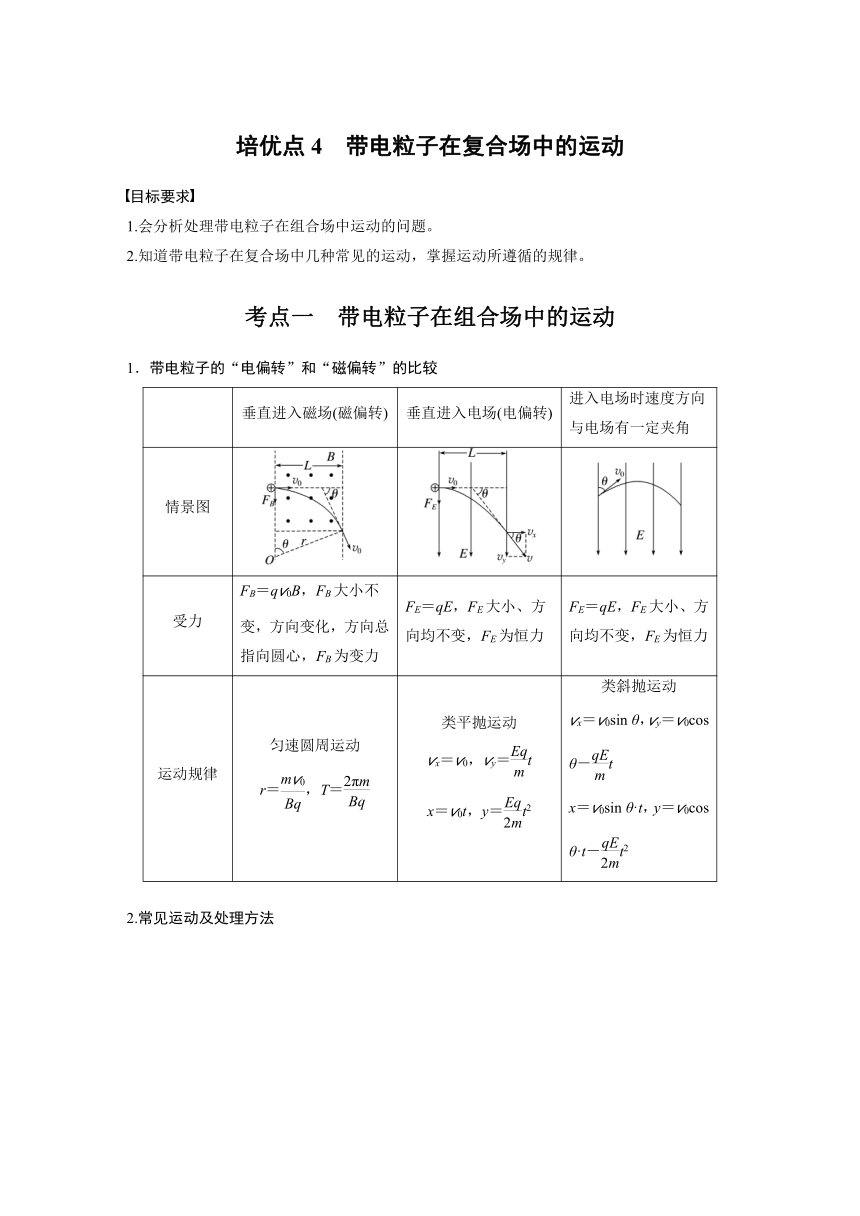 | |
| 格式 | docx | ||
| 文件大小 | 626.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-22 18:08:37 | ||
图片预览





文档简介
培优点4 带电粒子在复合场中的运动
目标要求
1.会分析处理带电粒子在组合场中运动的问题。
2.知道带电粒子在复合场中几种常见的运动,掌握运动所遵循的规律。
考点一 带电粒子在组合场中的运动
1.带电粒子的“电偏转”和“磁偏转”的比较
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
情景图
受力 FB=qv0B,FB大小不变,方向变化,方向总指向圆心,FB为变力 FE=qE,FE大小、方向均不变,FE为恒力 FE=qE,FE大小、方向均不变,FE为恒力
运动规律 匀速圆周运动 r=,T= 类平抛运动 vx=v0,vy=t x=v0t,y=t2 类斜抛运动 vx=v0sin θ,vy=v0cos θ-t x=v0sin θ·t,y=v0cos θ·t-t2
2.常见运动及处理方法
例1 (2023·江苏省模拟)如图所示,在xOy坐标系中,有垂直坐标平面向里的匀强磁场和沿y轴正向的匀强电场,匀强磁场的磁感应强度为B,电场和磁场的分界线为MN,MN穿过坐标原点和二、四象限,与y轴的夹角为θ=30°。一个质量为m、电荷量为q的带正电粒子,在坐标原点以大小为v0、方向与x轴正向成α=30°角的初速度射入磁场,粒子经磁场偏转进入电场后,恰好能到达x轴。不计粒子的重力,求:
(1)匀强电场的电场强度大小;
(2)粒子从O点射出后到第三次经过边界MN时,粒子运动的时间。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
例2 (2023·江苏扬州市一模)如图所示,第一象限内存在垂直于纸面向里的匀强磁场;第四象限内存在沿+y轴的匀强电场,电场强度大小为E=。t=0时刻,粒子从P点以速度v0平行+x轴射入电场,第1次通过x轴从Q点进入磁场。已知P点坐标为(0,-l),粒子质量为m、电荷量为+q,重力不计。
(1)求粒子经过Q点的速度v;
(2)欲使粒子不从y轴射出磁场,求磁感应强度的最小值Bm;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)若磁感应强度B=,求粒子第5次通过x轴的位置x和时间t。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
“5步”突破带电粒子在组合场中的运动问题
考点二 带电粒子在叠加场中的运动
1.三种典型情况
(1)若只有两个场,所受合力为零,则表现为匀速直线运动状态或静止状态。例如电场与磁场叠加满足qE=qvB时,重力场与磁场叠加满足mg=qvB时,重力场与电场叠加满足mg=qE时。
(2)若三场共存,所受合力为零时,粒子做匀速直线运动,其中洛伦兹力F=qvB的方向与速度v垂直。
(3)若三场共存,粒子做匀速圆周运动时,则有mg=qE,粒子在洛伦兹力作用下做匀速圆周运动,即qvB=m。
2.分析
例3 (2023·江苏卷·16)霍尔推进器某局部区域可抽象成如图所示的模型。Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B。质量为m、电荷量为e的电子从O点沿x轴正方向水平入射。入射速度为v0时,电子沿x轴做直线运动;入射速度小于v0时,电子的运动轨迹如图中的虚线所示,且在最高点与在最低点所受的合力大小相等。不计重力及电子间相互作用。
(1)求电场强度的大小E;
(2)若电子入射速度为,求运动到速度为时位置的纵坐标y1;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)若电子入射速度在0________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
配速法
配速法其实就是给物体配一个速度v,使得这个速度所产生的洛伦兹力与题目中的重力或者电场力(视情况而定)抵消,对应的,还会出现一个与v等大反向的速度v′,此时等效为只受到一个洛伦兹力,而不再是重力或者电场力加上洛伦兹力,从而降低分析难度。
(2023·江苏省高三期末调研)如图所示,在坐标原点有一粒子源,能以相同的初速度v0,向场区各方向辐射质量为m、电荷量为+q的带电粒子。x>0区域内存在n组相邻的匀强电场和匀强磁场,电场宽度为d,电场强度E=,方向水平向右;磁感应强度B=,方向垂直纸面向里。不计重力及粒子间的相互作用力。
(1)求进入第1组磁场区的粒子的速度大小v;
(2)调节磁场宽度,恰好使所有带电粒子都不能从第1组磁场的右边界穿出,求磁场的宽度Δx;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)保持该组合场条件不变,撤去粒子源,将另一带电粒子从O点由静止释放,若该带电粒子恰好不能穿过第n组磁场的右边界,求其比荷。
培优点4 带电粒子在复合场中的运动
例1 (1)Bv0 (2)
解析 (1)粒子在磁场中做匀速圆周运动,由牛顿第二定律可知qv0B=m
解得R=
粒子在磁场中运动的轨迹如图所示,根据几何关系,粒子出磁场的位置离x轴的距离为
y=Rsin 60°=
由于粒子进入电场后速度与电场方向相反,因此粒子做匀减速直线运动,刚好能到达x轴,根据动能定理有
-qEy=0-mv02,解得E=Bv0
(2)粒子在磁场中做匀速圆周运动的周期T=
第一次在磁场中运动的时间
t1=T=
在电场中运动时qE=ma
第一次在电场中运动的时间
t2=2=
第二次在磁场中运动的时间
t3=T=
则粒子从O点射出后到第三次经过边界MN时,粒子运动的时间t=t1+t2+t3=。
例2 (1)v0,与x轴正方向的夹角为45°
(2) (3)9l (10+)
解析 (1)粒子从P到Q做类平抛运动,轨迹如图甲所示,
根据动能定理qEl=mv2-mv02
解得v=v0,
设速度方向与x轴正方向夹角为α,根据几何关系cos α==
解得α=45°
(2)Q点到O点的距离s=2l,粒子进入磁场做匀速圆周运动,轨道半径为R,根据牛顿第二定律qvB=m可得B=
欲使粒子不从y轴射出磁场,临界状态轨迹如图甲中圆弧部分
根据几何关系R+Rsin α=2l,
解得R=2(2-)l
解得Bm=
(3)粒子进入磁场做匀速圆周运动,轨迹为圆周,
由r=得r=l,返回电场后做类斜抛运动,运动轨迹如图乙所示
第5次通过x轴时x=5s-2r=9l,
粒子在电场中的运动时间
t1=5×=,
粒子在磁场中的运动时间
t2=2××=,
解得t=t1+t2=(10+)。
例3 (1)v0B (2) (3)90%
解析 (1)由题知,入射速度为v0时,电子沿x轴做直线运动,则有Ee=ev0B
解得E=v0B
(2)电子在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场的复合场中,由于洛伦兹力不做功,且电子入射速度为,电子受到的电场力大于洛伦兹力,则电子向上偏转,
根据动能定理有
eEy1=m(v0)2-m(v0)2
解得y1=
(3)方法一 若电子以速度v入射时,设电子能到达的最高点位置的纵坐标为y,则根据动能定理有
eEy=mvm2-mv2
由于电子在最高点与在最低点所受的合力大小相等,则在最高点有F合=evmB-eE
在最低点有F合=eE-evB
联立有vm=-v=2v0-v
y=
要让电子到达纵坐标y2=位置,即y≥y2
解得v≤v0
则若电子入射速度在0 < v < v0范围内均匀分布,能到达纵坐标y2=位置的电子数N占总电子数N0的90%。
方法二 如果电子在复合场中受到的电场力与洛伦兹力等值反向,电子做匀速直线运动。如果这两个力不平衡,可将其分解为匀速直线运动和匀速圆周运动两个分运动。对于初状态静止的电子,设Ee=ev1B,可看作以v1=v0对应水平向右的匀速直线运动,而另一个分运动是v2=-v0,
根据洛伦兹力提供向心力,可得
Bev2=m
解得r==
设速度为v的电子,一个分运动为v1=v0,对应水平向右的匀速直线运动。另一个分运动的速度为v2,这个分运动做圆周运动的直径为y2,
则有=,
解得v2=。
电子入射速度为两个分速度的合速度,即v=v1-v2=v0-=。
在0由于电子在0高考预测
(1)2v0 (2)d (3)·
解析 (1)所有粒子到达第1组磁场区的速度大小v相同,由动能定理可得qEd=mv2-mv02
解得v=2v0
(2)粒子进入磁场时,速度方向与y轴负方向的夹角θ越小,粒子越容易射出磁场,θ的最小值为θ=60°
粒子在磁场中做圆周运动,满足
qvB=m
运动半径R==d
由几何关系可得Δx=R+Rcos θ
解得磁场的宽度Δx=d
(3)设粒子在第n层磁场中运动的速度为vn,轨迹半径为rn(下标表示粒子所在组数),
在电场中,根据动能定理有
nq′Ed=m′vn2
电场中,静电力不能改变粒子在y轴方向的动量,则从释放至恰好从第n组磁场返回,全过程中,在y轴方向,应用动量定理可得q′xBt=m′vn
又因为xt=nd
可解得=·
目标要求
1.会分析处理带电粒子在组合场中运动的问题。
2.知道带电粒子在复合场中几种常见的运动,掌握运动所遵循的规律。
考点一 带电粒子在组合场中的运动
1.带电粒子的“电偏转”和“磁偏转”的比较
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
情景图
受力 FB=qv0B,FB大小不变,方向变化,方向总指向圆心,FB为变力 FE=qE,FE大小、方向均不变,FE为恒力 FE=qE,FE大小、方向均不变,FE为恒力
运动规律 匀速圆周运动 r=,T= 类平抛运动 vx=v0,vy=t x=v0t,y=t2 类斜抛运动 vx=v0sin θ,vy=v0cos θ-t x=v0sin θ·t,y=v0cos θ·t-t2
2.常见运动及处理方法
例1 (2023·江苏省模拟)如图所示,在xOy坐标系中,有垂直坐标平面向里的匀强磁场和沿y轴正向的匀强电场,匀强磁场的磁感应强度为B,电场和磁场的分界线为MN,MN穿过坐标原点和二、四象限,与y轴的夹角为θ=30°。一个质量为m、电荷量为q的带正电粒子,在坐标原点以大小为v0、方向与x轴正向成α=30°角的初速度射入磁场,粒子经磁场偏转进入电场后,恰好能到达x轴。不计粒子的重力,求:
(1)匀强电场的电场强度大小;
(2)粒子从O点射出后到第三次经过边界MN时,粒子运动的时间。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
例2 (2023·江苏扬州市一模)如图所示,第一象限内存在垂直于纸面向里的匀强磁场;第四象限内存在沿+y轴的匀强电场,电场强度大小为E=。t=0时刻,粒子从P点以速度v0平行+x轴射入电场,第1次通过x轴从Q点进入磁场。已知P点坐标为(0,-l),粒子质量为m、电荷量为+q,重力不计。
(1)求粒子经过Q点的速度v;
(2)欲使粒子不从y轴射出磁场,求磁感应强度的最小值Bm;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)若磁感应强度B=,求粒子第5次通过x轴的位置x和时间t。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
“5步”突破带电粒子在组合场中的运动问题
考点二 带电粒子在叠加场中的运动
1.三种典型情况
(1)若只有两个场,所受合力为零,则表现为匀速直线运动状态或静止状态。例如电场与磁场叠加满足qE=qvB时,重力场与磁场叠加满足mg=qvB时,重力场与电场叠加满足mg=qE时。
(2)若三场共存,所受合力为零时,粒子做匀速直线运动,其中洛伦兹力F=qvB的方向与速度v垂直。
(3)若三场共存,粒子做匀速圆周运动时,则有mg=qE,粒子在洛伦兹力作用下做匀速圆周运动,即qvB=m。
2.分析
例3 (2023·江苏卷·16)霍尔推进器某局部区域可抽象成如图所示的模型。Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B。质量为m、电荷量为e的电子从O点沿x轴正方向水平入射。入射速度为v0时,电子沿x轴做直线运动;入射速度小于v0时,电子的运动轨迹如图中的虚线所示,且在最高点与在最低点所受的合力大小相等。不计重力及电子间相互作用。
(1)求电场强度的大小E;
(2)若电子入射速度为,求运动到速度为时位置的纵坐标y1;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)若电子入射速度在0
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
配速法
配速法其实就是给物体配一个速度v,使得这个速度所产生的洛伦兹力与题目中的重力或者电场力(视情况而定)抵消,对应的,还会出现一个与v等大反向的速度v′,此时等效为只受到一个洛伦兹力,而不再是重力或者电场力加上洛伦兹力,从而降低分析难度。
(2023·江苏省高三期末调研)如图所示,在坐标原点有一粒子源,能以相同的初速度v0,向场区各方向辐射质量为m、电荷量为+q的带电粒子。x>0区域内存在n组相邻的匀强电场和匀强磁场,电场宽度为d,电场强度E=,方向水平向右;磁感应强度B=,方向垂直纸面向里。不计重力及粒子间的相互作用力。
(1)求进入第1组磁场区的粒子的速度大小v;
(2)调节磁场宽度,恰好使所有带电粒子都不能从第1组磁场的右边界穿出,求磁场的宽度Δx;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)保持该组合场条件不变,撤去粒子源,将另一带电粒子从O点由静止释放,若该带电粒子恰好不能穿过第n组磁场的右边界,求其比荷。
培优点4 带电粒子在复合场中的运动
例1 (1)Bv0 (2)
解析 (1)粒子在磁场中做匀速圆周运动,由牛顿第二定律可知qv0B=m
解得R=
粒子在磁场中运动的轨迹如图所示,根据几何关系,粒子出磁场的位置离x轴的距离为
y=Rsin 60°=
由于粒子进入电场后速度与电场方向相反,因此粒子做匀减速直线运动,刚好能到达x轴,根据动能定理有
-qEy=0-mv02,解得E=Bv0
(2)粒子在磁场中做匀速圆周运动的周期T=
第一次在磁场中运动的时间
t1=T=
在电场中运动时qE=ma
第一次在电场中运动的时间
t2=2=
第二次在磁场中运动的时间
t3=T=
则粒子从O点射出后到第三次经过边界MN时,粒子运动的时间t=t1+t2+t3=。
例2 (1)v0,与x轴正方向的夹角为45°
(2) (3)9l (10+)
解析 (1)粒子从P到Q做类平抛运动,轨迹如图甲所示,
根据动能定理qEl=mv2-mv02
解得v=v0,
设速度方向与x轴正方向夹角为α,根据几何关系cos α==
解得α=45°
(2)Q点到O点的距离s=2l,粒子进入磁场做匀速圆周运动,轨道半径为R,根据牛顿第二定律qvB=m可得B=
欲使粒子不从y轴射出磁场,临界状态轨迹如图甲中圆弧部分
根据几何关系R+Rsin α=2l,
解得R=2(2-)l
解得Bm=
(3)粒子进入磁场做匀速圆周运动,轨迹为圆周,
由r=得r=l,返回电场后做类斜抛运动,运动轨迹如图乙所示
第5次通过x轴时x=5s-2r=9l,
粒子在电场中的运动时间
t1=5×=,
粒子在磁场中的运动时间
t2=2××=,
解得t=t1+t2=(10+)。
例3 (1)v0B (2) (3)90%
解析 (1)由题知,入射速度为v0时,电子沿x轴做直线运动,则有Ee=ev0B
解得E=v0B
(2)电子在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场的复合场中,由于洛伦兹力不做功,且电子入射速度为,电子受到的电场力大于洛伦兹力,则电子向上偏转,
根据动能定理有
eEy1=m(v0)2-m(v0)2
解得y1=
(3)方法一 若电子以速度v入射时,设电子能到达的最高点位置的纵坐标为y,则根据动能定理有
eEy=mvm2-mv2
由于电子在最高点与在最低点所受的合力大小相等,则在最高点有F合=evmB-eE
在最低点有F合=eE-evB
联立有vm=-v=2v0-v
y=
要让电子到达纵坐标y2=位置,即y≥y2
解得v≤v0
则若电子入射速度在0 < v < v0范围内均匀分布,能到达纵坐标y2=位置的电子数N占总电子数N0的90%。
方法二 如果电子在复合场中受到的电场力与洛伦兹力等值反向,电子做匀速直线运动。如果这两个力不平衡,可将其分解为匀速直线运动和匀速圆周运动两个分运动。对于初状态静止的电子,设Ee=ev1B,可看作以v1=v0对应水平向右的匀速直线运动,而另一个分运动是v2=-v0,
根据洛伦兹力提供向心力,可得
Bev2=m
解得r==
设速度为v的电子,一个分运动为v1=v0,对应水平向右的匀速直线运动。另一个分运动的速度为v2,这个分运动做圆周运动的直径为y2,
则有=,
解得v2=。
电子入射速度为两个分速度的合速度,即v=v1-v2=v0-=。
在0
(1)2v0 (2)d (3)·
解析 (1)所有粒子到达第1组磁场区的速度大小v相同,由动能定理可得qEd=mv2-mv02
解得v=2v0
(2)粒子进入磁场时,速度方向与y轴负方向的夹角θ越小,粒子越容易射出磁场,θ的最小值为θ=60°
粒子在磁场中做圆周运动,满足
qvB=m
运动半径R==d
由几何关系可得Δx=R+Rcos θ
解得磁场的宽度Δx=d
(3)设粒子在第n层磁场中运动的速度为vn,轨迹半径为rn(下标表示粒子所在组数),
在电场中,根据动能定理有
nq′Ed=m′vn2
电场中,静电力不能改变粒子在y轴方向的动量,则从释放至恰好从第n组磁场返回,全过程中,在y轴方向,应用动量定理可得q′xBt=m′vn
又因为xt=nd
可解得=·
同课章节目录
