第24章相似形的复习
图片预览

文档简介
第24章相似形的复习
班级 姓名 座号
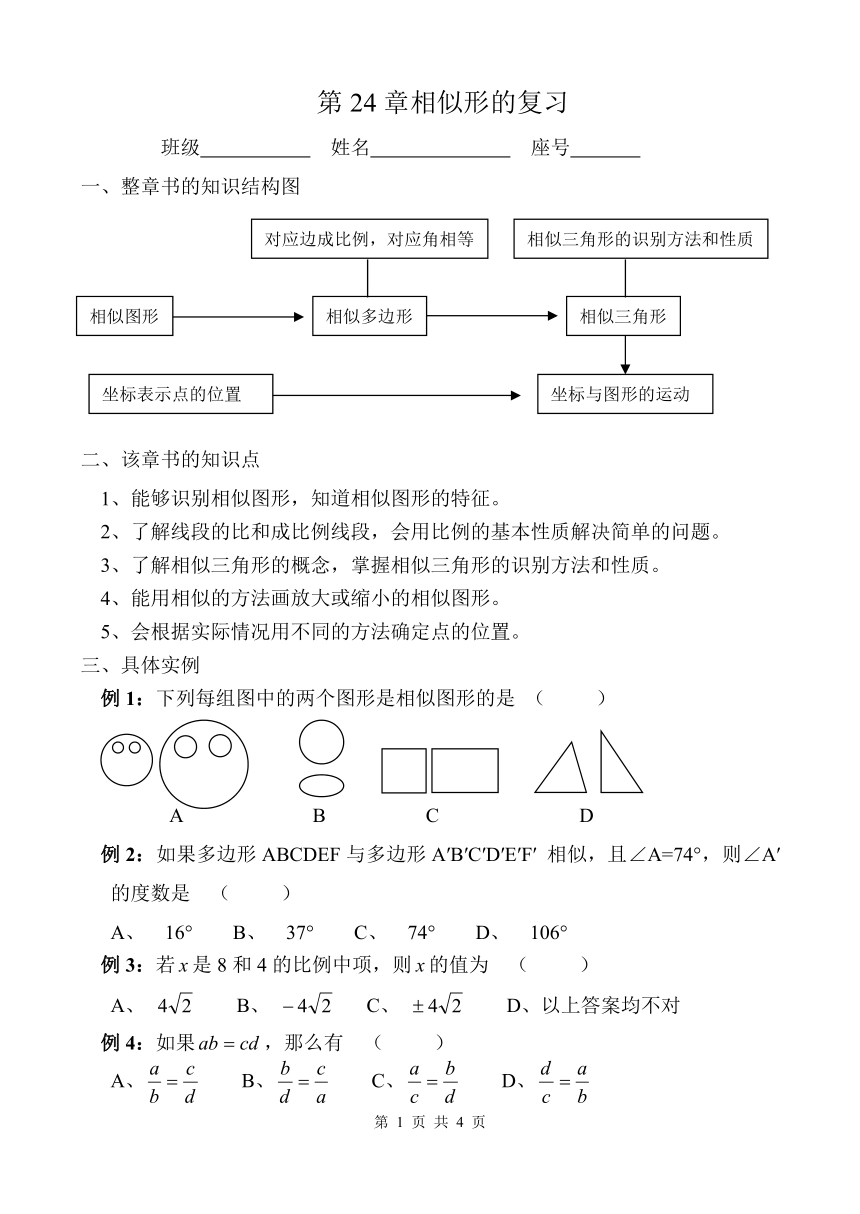
1、 整章书的知识结构图
二、该章书的知识点
1、能够识别相似图形,知道相似图形的特征。
2、了解线段的比和成比例线段,会用比例的基本性质解决简单的问题。
3、了解相似三角形的概念,掌握相似三角形的识别方法和性质。
4、能用相似的方法画放大或缩小的相似图形。
5、会根据实际情况用不同的方法确定点的位置。
三、具体实例
例1:下列每组图中的两个图形是相似图形的是 ( )
A B C D
例2:如果多边形ABCDEF与多边形A′B′C′D′E′F′ 相似,且∠A=74°,则∠A′的度数是 ( )
A、 16° B、 37° C、 74° D、 106°
例3:若是8和4的比例中项,则的值为 ( )
A、 B、 C、 D、以上答案均不对
例4:如果,那么有 ( )
A、 B、 C、 D、
例5:相似三角形的识别与性质的运用
1、三角形相似的条件
(1) ,两三角形相似.
(2) ,两三角形相似.
(3) ,两三角形相似.
2、如何寻找和发现相似三角形
两个三角形相似,一般说来必须具备下列六种图形之一:
只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决。
3、相似三角形与相似多边形的性质
(1)相似三角形的性质
①相似三角形的三边 ,三角 。
②相似三角形的 , 与 都等于相似比。
③相似三角形周长之比等于 ,相似三角形面积之比等于 。
(2)相似多边形的性质
①相似多边形的对应边 ,对应角 .
②相似多边形的对角线之比、周长之比都等于 .
③相似多边形面积之比等于 .
4、几何变换(按一定的方法把一个图形变成另一个图形)
(1)相似变换:保持图形的形状不变的几何变换叫做相似变换
(2)位似变换:位似图形:如果两个图形不仅是 图形,而且每组对应点所在的直线都 ,那么这样的两个图形叫做位似图形,这个点叫做 ,这时的相似比又称为 。
5、相关题型
(1)在相同时刻的物高与影长成比例,如果高为1.5米的测竿的影长为2.5米,那么影长为30米的旗杆的高是( )
A、 20米 B、 18米 C、 16米 D、 15米
(2)如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使ΔABE和ΔACD相似的是( )
A、 ∠B=∠C B、 ∠ADC=∠AEB
C、BE=CD,AB=AC D、 AD∶AC=AE∶AB
(3)两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积之和为130cm2,那么较小的多边形的面积是 cm2.
(4)如图,DE与BC不平行,当= 时,
ΔABC与ΔADE相似。
(5)如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长。
(6)如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m。求AB的长。
例6:请同学们设法把四边形ABCD缩小为原来的。
例7:如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由。(10分)
相似图形
相似多边形
对应边成比例,对应角相等
相似三角形
相似三角形的识别方法和性质
坐标与图形的运动
坐标表示点的位置
第 1 页 共 4 页
班级 姓名 座号
1、 整章书的知识结构图
二、该章书的知识点
1、能够识别相似图形,知道相似图形的特征。
2、了解线段的比和成比例线段,会用比例的基本性质解决简单的问题。
3、了解相似三角形的概念,掌握相似三角形的识别方法和性质。
4、能用相似的方法画放大或缩小的相似图形。
5、会根据实际情况用不同的方法确定点的位置。
三、具体实例
例1:下列每组图中的两个图形是相似图形的是 ( )
A B C D
例2:如果多边形ABCDEF与多边形A′B′C′D′E′F′ 相似,且∠A=74°,则∠A′的度数是 ( )
A、 16° B、 37° C、 74° D、 106°
例3:若是8和4的比例中项,则的值为 ( )
A、 B、 C、 D、以上答案均不对
例4:如果,那么有 ( )
A、 B、 C、 D、
例5:相似三角形的识别与性质的运用
1、三角形相似的条件
(1) ,两三角形相似.
(2) ,两三角形相似.
(3) ,两三角形相似.
2、如何寻找和发现相似三角形
两个三角形相似,一般说来必须具备下列六种图形之一:
只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决。
3、相似三角形与相似多边形的性质
(1)相似三角形的性质
①相似三角形的三边 ,三角 。
②相似三角形的 , 与 都等于相似比。
③相似三角形周长之比等于 ,相似三角形面积之比等于 。
(2)相似多边形的性质
①相似多边形的对应边 ,对应角 .
②相似多边形的对角线之比、周长之比都等于 .
③相似多边形面积之比等于 .
4、几何变换(按一定的方法把一个图形变成另一个图形)
(1)相似变换:保持图形的形状不变的几何变换叫做相似变换
(2)位似变换:位似图形:如果两个图形不仅是 图形,而且每组对应点所在的直线都 ,那么这样的两个图形叫做位似图形,这个点叫做 ,这时的相似比又称为 。
5、相关题型
(1)在相同时刻的物高与影长成比例,如果高为1.5米的测竿的影长为2.5米,那么影长为30米的旗杆的高是( )
A、 20米 B、 18米 C、 16米 D、 15米
(2)如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使ΔABE和ΔACD相似的是( )
A、 ∠B=∠C B、 ∠ADC=∠AEB
C、BE=CD,AB=AC D、 AD∶AC=AE∶AB
(3)两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积之和为130cm2,那么较小的多边形的面积是 cm2.
(4)如图,DE与BC不平行,当= 时,
ΔABC与ΔADE相似。
(5)如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长。
(6)如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m。求AB的长。
例6:请同学们设法把四边形ABCD缩小为原来的。
例7:如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由。(10分)
相似图形
相似多边形
对应边成比例,对应角相等
相似三角形
相似三角形的识别方法和性质
坐标与图形的运动
坐标表示点的位置
第 1 页 共 4 页
同课章节目录
