相似三角形的性质综合、拓展练习
图片预览
文档简介
相似三角形的性质综合、拓展练习
综合练习
1.选择题
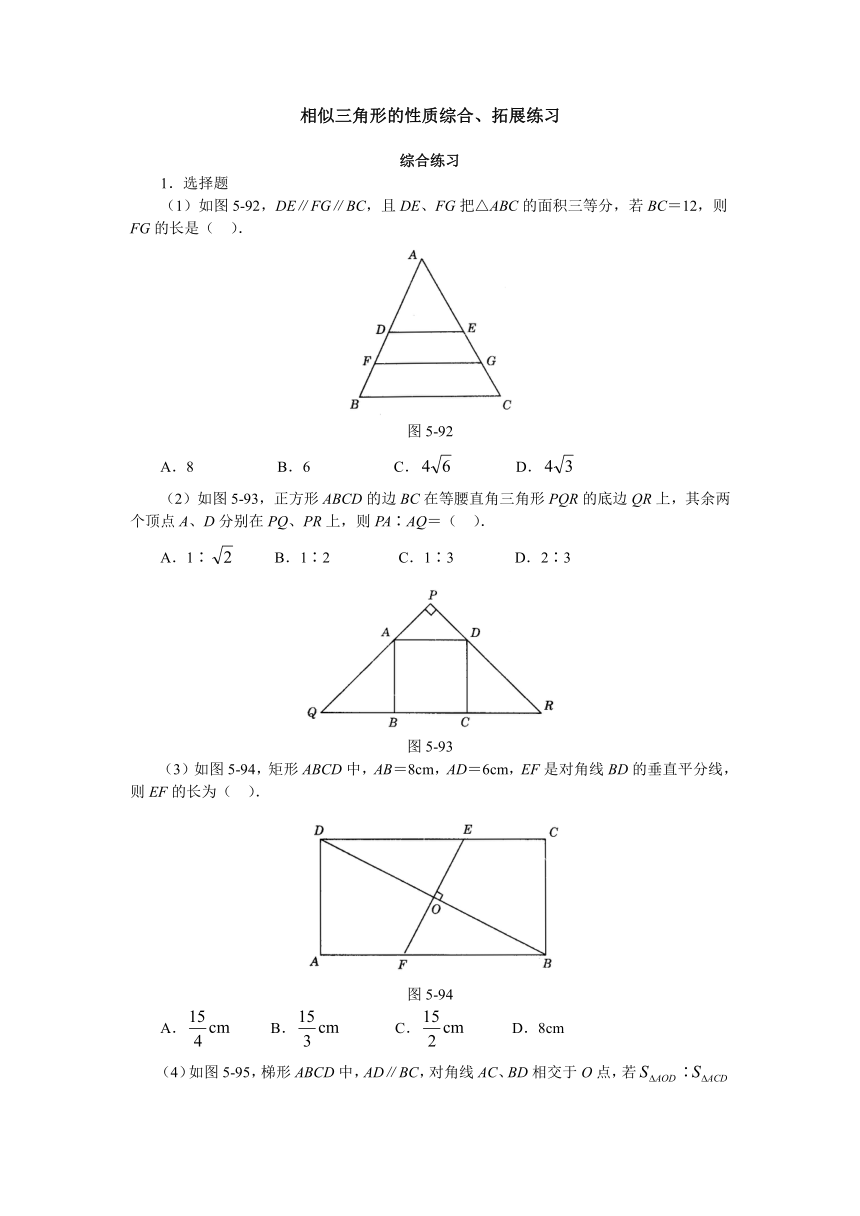
(1)如图5-92,DE∥FG∥BC,且DE、FG把△ABC的面积三等分,若BC=12,则FG的长是( ).
图5-92
A.8 B.6 C. D.
(2)如图5-93,正方形ABCD的边BC在等腰直角三角形PQR的底边QR上,其余两个顶点A、D分别在PQ、PR上,则PA∶AQ=( ).
A.1∶ B.1∶2 C.1∶3 D.2∶3
图5-93
(3)如图5-94,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( ).
图5-94
A. B. C. D.8cm
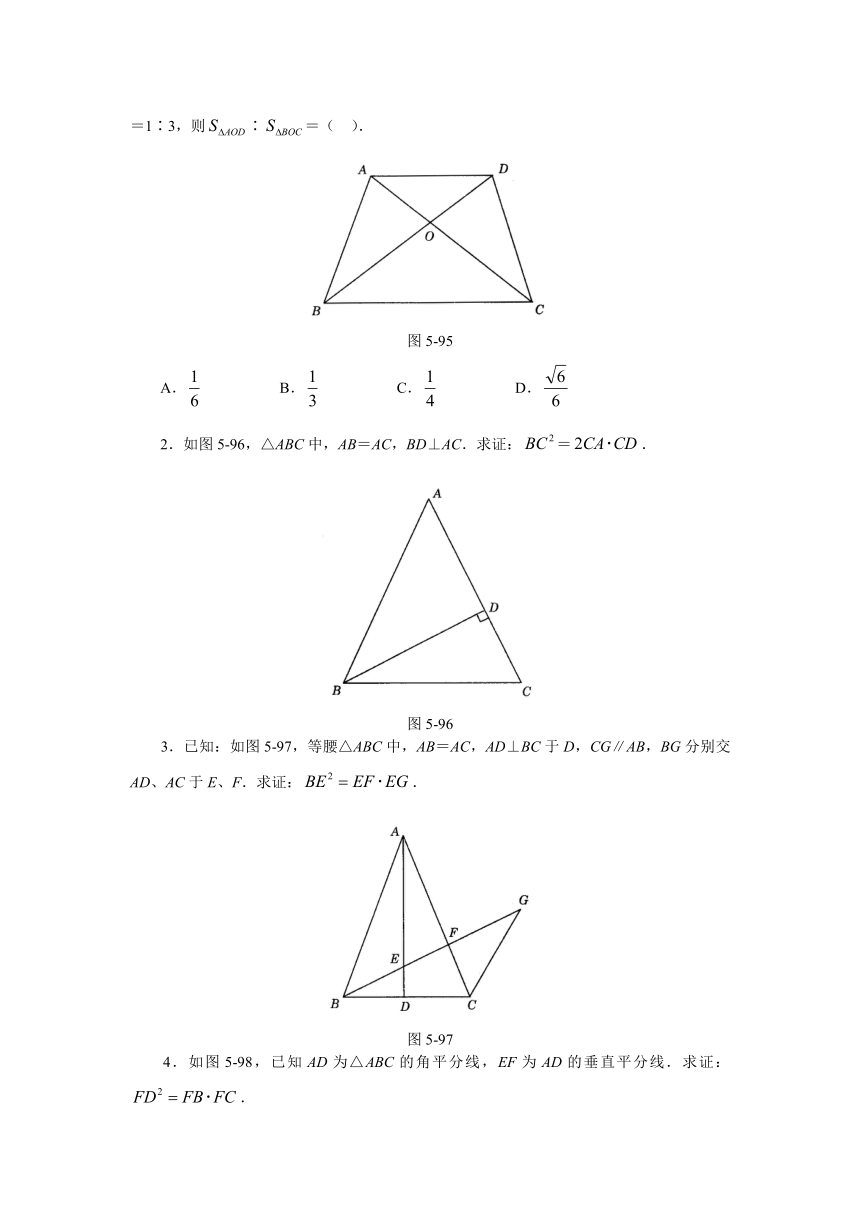
(4)如图5-95,梯形ABCD中,AD∥BC,对角线AC、BD相交于O点,若∶=1∶3,则∶=( ).
图5-95
A. B. C. D.
2.如图5-96,△ABC中,AB=AC,BD⊥AC.求证:=.
图5-96
3.已知:如图5-97,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:.
图5-97
4.如图5-98,已知AD为△ABC的角平分线,EF为AD的垂直平分线.求证:.
图5-98
5.如图5-99,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.求证:.
图5-99
6.已知:△ABC中,∠BAC=135°,D、E在BC上(D在B、E之间),且AD=AE,∠DAE=90°,求证:(1),(2)∶=BD∶CE.
7.已知:△ABC中,∠BAC=120°,D、E在BC上(D在B、E之间),且∠DAE=60°,AD=AE.求证:(1),(2)
拓展练习
1.如图5-100,在矩形ABCD中,AN⊥BD,N为垂足,NF⊥CD,NE⊥BC,垂足分别为E、F.
求证:
图5-100
2.如图5-101,在梯形ABCD中,AB∥DC,CE是∠BCD的平分线,且CE⊥AD,DE=2AE,CE把梯形分成面积为和两部分,若=1,求.
图5-101
3.已知:如图5-102,在△ABC中,∠ACB=90°,M是BC的中点,CN⊥AM,垂足是N,求证:.
图5-102
4.已知:如图5-103,梯形ABCD,DC∥AB,在下底AB上取AE=EF,连结DE、CF并延长交于点G,AC与DG交于点M,求证:.
图5-103
5.如图5-104,△ABC中,AB=AC,∠A=90°,,.求证:∠ADE=∠EBC.
图5-104
6.如图5-105,△ABC内有一点K,过K引三边的平行线与三边交成的线段,有同一长度x,如果BC、AC、AB长度分别为a、b、c,试求x.
图5-105
参考答案
综合练习
1.(1)C (2)B (3)C (4)C
2.略 3.略 4.略 5.略 6.略 7.略
拓展练习
1.略
2.过B作BF∥AD交CD于F,交CE于M,则BM=FM=AD再延长,CB、DA,得
3.略 4.略 5.略
6.
综合练习
1.选择题
(1)如图5-92,DE∥FG∥BC,且DE、FG把△ABC的面积三等分,若BC=12,则FG的长是( ).
图5-92
A.8 B.6 C. D.
(2)如图5-93,正方形ABCD的边BC在等腰直角三角形PQR的底边QR上,其余两个顶点A、D分别在PQ、PR上,则PA∶AQ=( ).
A.1∶ B.1∶2 C.1∶3 D.2∶3
图5-93
(3)如图5-94,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( ).
图5-94
A. B. C. D.8cm
(4)如图5-95,梯形ABCD中,AD∥BC,对角线AC、BD相交于O点,若∶=1∶3,则∶=( ).
图5-95
A. B. C. D.
2.如图5-96,△ABC中,AB=AC,BD⊥AC.求证:=.
图5-96
3.已知:如图5-97,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:.
图5-97
4.如图5-98,已知AD为△ABC的角平分线,EF为AD的垂直平分线.求证:.
图5-98
5.如图5-99,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.求证:.
图5-99
6.已知:△ABC中,∠BAC=135°,D、E在BC上(D在B、E之间),且AD=AE,∠DAE=90°,求证:(1),(2)∶=BD∶CE.
7.已知:△ABC中,∠BAC=120°,D、E在BC上(D在B、E之间),且∠DAE=60°,AD=AE.求证:(1),(2)
拓展练习
1.如图5-100,在矩形ABCD中,AN⊥BD,N为垂足,NF⊥CD,NE⊥BC,垂足分别为E、F.
求证:
图5-100
2.如图5-101,在梯形ABCD中,AB∥DC,CE是∠BCD的平分线,且CE⊥AD,DE=2AE,CE把梯形分成面积为和两部分,若=1,求.
图5-101
3.已知:如图5-102,在△ABC中,∠ACB=90°,M是BC的中点,CN⊥AM,垂足是N,求证:.
图5-102
4.已知:如图5-103,梯形ABCD,DC∥AB,在下底AB上取AE=EF,连结DE、CF并延长交于点G,AC与DG交于点M,求证:.
图5-103
5.如图5-104,△ABC中,AB=AC,∠A=90°,,.求证:∠ADE=∠EBC.
图5-104
6.如图5-105,△ABC内有一点K,过K引三边的平行线与三边交成的线段,有同一长度x,如果BC、AC、AB长度分别为a、b、c,试求x.
图5-105
参考答案
综合练习
1.(1)C (2)B (3)C (4)C
2.略 3.略 4.略 5.略 6.略 7.略
拓展练习
1.略
2.过B作BF∥AD交CD于F,交CE于M,则BM=FM=AD再延长,CB、DA,得
3.略 4.略 5.略
6.
