第五章 圆 (第1-4节)阶段性测试题(含答案)
文档属性
| 名称 | 第五章 圆 (第1-4节)阶段性测试题(含答案) | 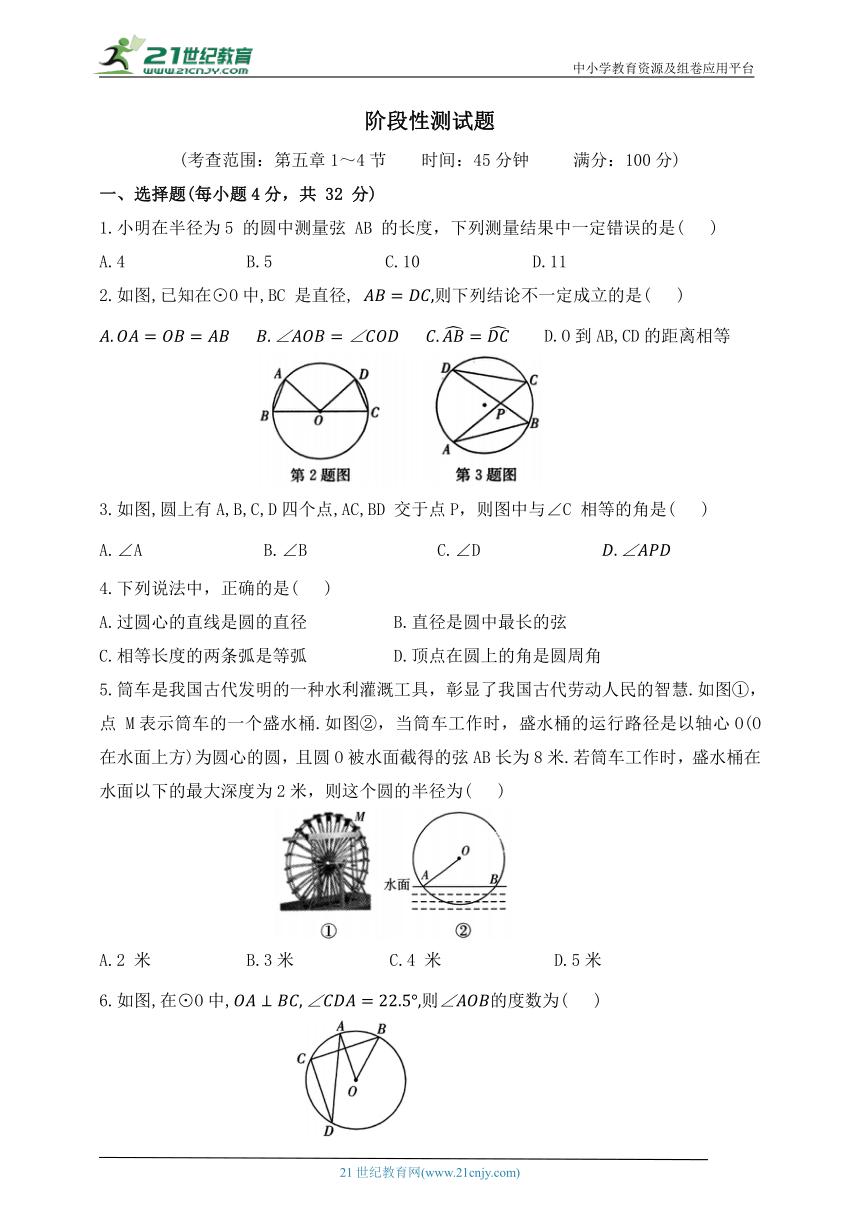 | |
| 格式 | docx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 13:28:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
阶段性测试题
(考查范围:第五章1~4节 时间:45分钟 满分:100分)
一、选择题(每小题4分,共 32 分)
1.小明在半径为5 的圆中测量弦 AB 的长度,下列测量结果中一定错误的是( )
A.4 B.5 C.10 D.11
2.如图,已知在⊙O中,BC 是直径, 则下列结论不一定成立的是( )
D.O到AB,CD的距离相等
3.如图,圆上有A,B,C,D四个点,AC,BD 交于点P,则图中与∠C 相等的角是( )
A.∠A B.∠B C.∠D
4.下列说法中,正确的是( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.顶点在圆上的角是圆周角
5.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图①,点 M表示筒车的一个盛水桶.如图②,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且圆O被水面截得的弦AB长为8米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆的半径为( )
A.2 米 B.3米 C.4 米 D.5米
6.如图,在⊙O中,则的度数为( )
7.如图,已知锐角 按如下步骤作图:①在射线OA 上取一点C,以点O为圆心,OC长为半径作 PQ, 交射线 OB 于点 D,连接CD;②分别以点 C,D为圆心,CD 长为半径作弧,交于点 M,N;③连接 OM,MN,ND.根据以上作图过程及所作图形,下列结论中错误的是( )
B.若 则
∥
8.学了圆后,小亮突发奇想,想到用这种方法测量三角形的角度:将三角形纸片如图放置,使得顶点 C 在量角器的半圆上,纸片另外两边分别与量角器交于A,B两点.点A,B的度数是 这样小明就能得到 的度数.请你帮忙算算∠C 的度数是( )
二、填空题(每小题5 分,共 40分)
9.战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于____________.
10.如图,在⊙O中,AB 为弦,直线 于点C,交⊙O 于点 D,E,连接EA,EB,则图中存在的相等关系有__________.(写出两组即可)
11.如图是一个圆形人工湖,弦AB 是湖上的一座桥.已知圆的半径是 20 米,圆周角 则AB 的长为__________米.
12.如图,点B,E在半圆O上,四边形OABC 和四边形ODEF 均为矩形.若
则DF 的长为___________.
13. 如图,在⊙O 中, 则 AC________2CD.(填“>”“<”或“=”)
14.如图,在正方形网格中,每个小正方形的边长都是1,以AB 为直径的⊙O上有两点C,D.点A,B,C在网格线的交点上,则 的值是__________.
15.如图所示,在车轮上取A,B 两点,设 所在圆的圆心为O,半径为 r cm.作弦AB 的垂线OC,D为垂足,经测量, 则此车轮半径为__________cm.
16.我国古代数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两个钉子的内侧,转动“矩”,则“矩”的顶点 C 的运动路线将会是一个圆.依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:______
___________________________________________________________________________.
三、解答题(共28分)
17.(8分)如图, M,N 分别是半径OA,OB 的中点.求证:CM=CN.
18.(10 分)如图,AB 为⊙O 的直径,D 是弦AC 延长线上一点, DB 的延长线交⊙O 于点 E,连接CE.
(1)求证:
(2)若 的度数为 求 的度数.
19.(10分)如图,⊙O 的半径为 2,弦. A 是弦BC所对优弧上的一个点,连接CO并延长交⊙O 于点M,连接AM,过点 B 作. AC,垂足为 E.
(1)求证: ∥
(2)过点 A 作 分别交 BE,BC 于点 H,D.求 AH 的长.
参考答案
1. D 2. A 3. B 4. B 5. D 6. C 7. B 8. B
9.半径
(答案不唯一)
11.20 12.5 13.< 15.75
16.圆是所有到定点的距离等于定长的点的集合
17.证明:在⊙O中,
∵OA=OB,M,N分别是半径OA,OB 的中点,
在 和 中,
∴CM=CN.
18.(1)证明:如图,连接 BC.
∵AB 是⊙O的直径, ∴AD⊥BC.又AC=CD,∴AB=BD,∴∠A=∠D.
(2)解: 的度数为 108°,∴∠EBA=54°.
又∠EBA=∠A+∠D,∠A=∠D,∴∠A=
19.(1)证明:∵MC 是圆的直径,
∥
(2)解:如图,连接 MB.∵MC 是圆的直径,∴∠MBC=90°,∴MB⊥BC.
∵AD⊥BC,∴BM∥AD.
∵BE∥MA,∴四边形AMBH 是平行四边形, ∴AH=MB.
∵圆的半径是2,∴MC=4,∴MB=∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
阶段性测试题
(考查范围:第五章1~4节 时间:45分钟 满分:100分)
一、选择题(每小题4分,共 32 分)
1.小明在半径为5 的圆中测量弦 AB 的长度,下列测量结果中一定错误的是( )
A.4 B.5 C.10 D.11
2.如图,已知在⊙O中,BC 是直径, 则下列结论不一定成立的是( )
D.O到AB,CD的距离相等
3.如图,圆上有A,B,C,D四个点,AC,BD 交于点P,则图中与∠C 相等的角是( )
A.∠A B.∠B C.∠D
4.下列说法中,正确的是( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.顶点在圆上的角是圆周角
5.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图①,点 M表示筒车的一个盛水桶.如图②,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且圆O被水面截得的弦AB长为8米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆的半径为( )
A.2 米 B.3米 C.4 米 D.5米
6.如图,在⊙O中,则的度数为( )
7.如图,已知锐角 按如下步骤作图:①在射线OA 上取一点C,以点O为圆心,OC长为半径作 PQ, 交射线 OB 于点 D,连接CD;②分别以点 C,D为圆心,CD 长为半径作弧,交于点 M,N;③连接 OM,MN,ND.根据以上作图过程及所作图形,下列结论中错误的是( )
B.若 则
∥
8.学了圆后,小亮突发奇想,想到用这种方法测量三角形的角度:将三角形纸片如图放置,使得顶点 C 在量角器的半圆上,纸片另外两边分别与量角器交于A,B两点.点A,B的度数是 这样小明就能得到 的度数.请你帮忙算算∠C 的度数是( )
二、填空题(每小题5 分,共 40分)
9.战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于____________.
10.如图,在⊙O中,AB 为弦,直线 于点C,交⊙O 于点 D,E,连接EA,EB,则图中存在的相等关系有__________.(写出两组即可)
11.如图是一个圆形人工湖,弦AB 是湖上的一座桥.已知圆的半径是 20 米,圆周角 则AB 的长为__________米.
12.如图,点B,E在半圆O上,四边形OABC 和四边形ODEF 均为矩形.若
则DF 的长为___________.
13. 如图,在⊙O 中, 则 AC________2CD.(填“>”“<”或“=”)
14.如图,在正方形网格中,每个小正方形的边长都是1,以AB 为直径的⊙O上有两点C,D.点A,B,C在网格线的交点上,则 的值是__________.
15.如图所示,在车轮上取A,B 两点,设 所在圆的圆心为O,半径为 r cm.作弦AB 的垂线OC,D为垂足,经测量, 则此车轮半径为__________cm.
16.我国古代数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两个钉子的内侧,转动“矩”,则“矩”的顶点 C 的运动路线将会是一个圆.依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:______
___________________________________________________________________________.
三、解答题(共28分)
17.(8分)如图, M,N 分别是半径OA,OB 的中点.求证:CM=CN.
18.(10 分)如图,AB 为⊙O 的直径,D 是弦AC 延长线上一点, DB 的延长线交⊙O 于点 E,连接CE.
(1)求证:
(2)若 的度数为 求 的度数.
19.(10分)如图,⊙O 的半径为 2,弦. A 是弦BC所对优弧上的一个点,连接CO并延长交⊙O 于点M,连接AM,过点 B 作. AC,垂足为 E.
(1)求证: ∥
(2)过点 A 作 分别交 BE,BC 于点 H,D.求 AH 的长.
参考答案
1. D 2. A 3. B 4. B 5. D 6. C 7. B 8. B
9.半径
(答案不唯一)
11.20 12.5 13.< 15.75
16.圆是所有到定点的距离等于定长的点的集合
17.证明:在⊙O中,
∵OA=OB,M,N分别是半径OA,OB 的中点,
在 和 中,
∴CM=CN.
18.(1)证明:如图,连接 BC.
∵AB 是⊙O的直径, ∴AD⊥BC.又AC=CD,∴AB=BD,∴∠A=∠D.
(2)解: 的度数为 108°,∴∠EBA=54°.
又∠EBA=∠A+∠D,∠A=∠D,∴∠A=
19.(1)证明:∵MC 是圆的直径,
∥
(2)解:如图,连接 MB.∵MC 是圆的直径,∴∠MBC=90°,∴MB⊥BC.
∵AD⊥BC,∴BM∥AD.
∵BE∥MA,∴四边形AMBH 是平行四边形, ∴AH=MB.
∵圆的半径是2,∴MC=4,∴MB=∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
