13.3实数(1)
图片预览







文档简介
课件24张PPT。13.3实数(1)想一想 使用计算器计算,把下列各数写成小数的形式,你有什么发现? 事实上,任何一个有理数都可以写成有限小数或无限循环小数。反过来,任何有限小数或无限循环小数也都是有理数
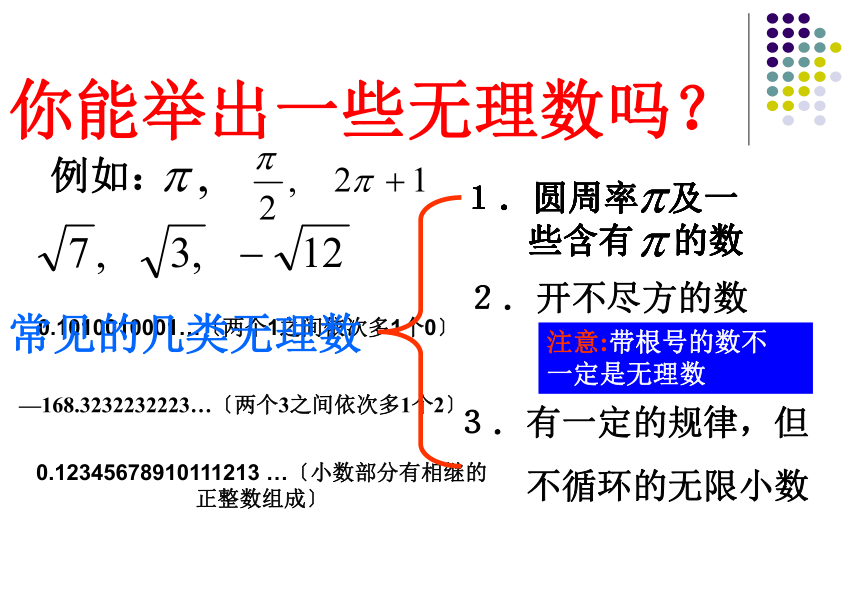
活动1你所认识的数中有没有不属于有理数的呢?说说看!叫做无理数.新知=1.41421356237309504880168… =1.73205080756887729352744…π=3.1415926535897932384626… 1.010010001…(两个1之间依次多一个0)无限不循环小数无理数的概念无理数也像有理数一样广泛存在着。
无理数也有正负之分,例如正无理数:
负无理数:———你能举出一些无理数吗?2.开不尽方的数例如:注意:带根号的数不
一定是无理数3.有一定的规律,但
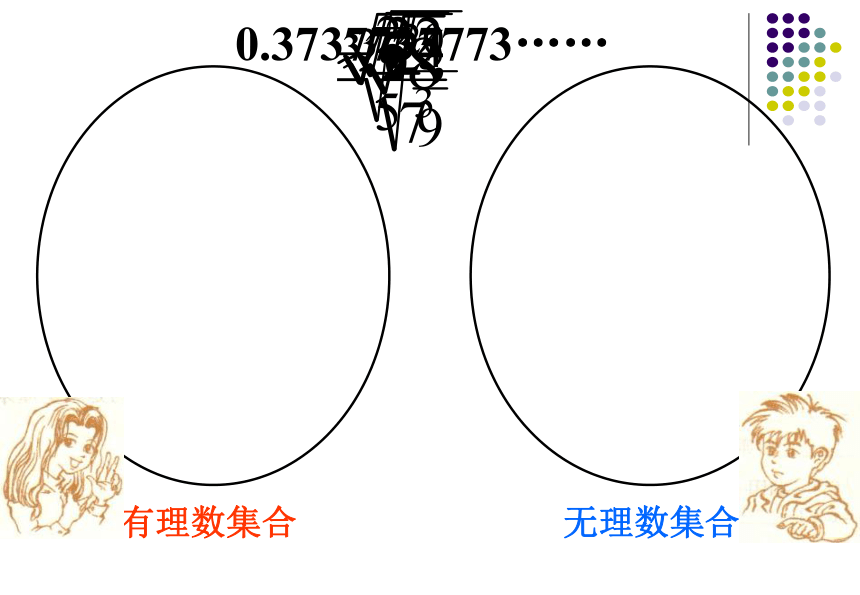
不循环的无限小数常见的几类无理数有理数集合无理数集合0.3737737773……0 有理数和无理数统称为实数(real number) 所有实数组成的集合叫作实数集由上可知:
1.实数可分为哪两类数?探究实数的分类(一)2.有理数可分为哪几类?3.无理数可分为哪几类?活动2⑧ ① ② ③ ④ ⑤ ⑥ ⑦ 依据实数的分类(一)示意图,在右图的卡片上填上下列数的名称.你发现实数的分类示意图与这棵树枝干的形状有哪些联系吗?正有理数零负有理数正无理数负无理数有理数无理数实数活动2探究实数的分类(二)活动3 依据实数的分类(二)示意图,在右图的卡片上填上下列数的名称.你发现实数的分类示意图与这棵树枝干的形状有哪些联系吗? ①②实数③④⑤⑥⑦⑧正实数零负实数正有理数正无理数负有理数负无理数活动3判断下列说法是否正确,并说明理由: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?无理数 可以用数轴上的点来表示.A问题2.你能在数轴上表示出 吗?问题1.无理数能在数轴上表示出来吗?活动4- 每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。实数和数轴上的点是一一对应的.1.判断:(1)实数不是有理数就是无理数;( )(2)无理数都是无限不循环小数;( )(3)无理数都是无限小数; ( )(4)带根号的数都是无理数; ( )(5)无理数一定都带根号. ( )×× 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数.探索新知⑸│ - 1 │= 。⑴a是一个实数,它的相反数为 ;⑵如果a≠0,那么它的倒数为 ;⑶ a是一个正数,它的绝对值为 ;⑷ a是一个负数,它的绝对值为 ;-aa-a想一想-1(6)绝对值最小的实数是______02、填空:
(1) 的相反数是__________ (5) 绝对值是 _________ (2) 的倒数是____,(3)| |=___________(4)绝对值等于 的数是 _________ 的平方 是___ .(6)绝对值小于 的整数是___________★实数和数轴上的点是一一对应的. ★有序实数对和直角坐标系中的点是一 一对应的. 约公元600年,毕达哥拉斯学派认为宇宙万物
的总规律是服从整数化,认为世界上一切现象,都
能归结为整数或整数之比。正当毕氏学派津津乐道
地高唱“万物皆数”时,该学派的一位成员希伯索斯
利用推理的方法发现,正方形对角线与其一边之比
既不是整数,也不是分数。海神错判数学故事: 这个发现被当时的人们看成是“荒谬”和违反
常识的事。对于只有整数和整数比概念的他们来
说,这意味着正方形对角线与其一边之比竟然不
能用任何“数”来表示!这在数学史上称为第一次
数学危机。最后希伯索斯的发现没有被毕达哥拉
斯学派的信徒所接受,相传就因为这一发现,毕
达哥拉斯学派把希伯索斯投入大海中处死。海神错判数学故事:谢谢
活动1你所认识的数中有没有不属于有理数的呢?说说看!叫做无理数.新知=1.41421356237309504880168… =1.73205080756887729352744…π=3.1415926535897932384626… 1.010010001…(两个1之间依次多一个0)无限不循环小数无理数的概念无理数也像有理数一样广泛存在着。
无理数也有正负之分,例如正无理数:
负无理数:———你能举出一些无理数吗?2.开不尽方的数例如:注意:带根号的数不
一定是无理数3.有一定的规律,但
不循环的无限小数常见的几类无理数有理数集合无理数集合0.3737737773……0 有理数和无理数统称为实数(real number) 所有实数组成的集合叫作实数集由上可知:
1.实数可分为哪两类数?探究实数的分类(一)2.有理数可分为哪几类?3.无理数可分为哪几类?活动2⑧ ① ② ③ ④ ⑤ ⑥ ⑦ 依据实数的分类(一)示意图,在右图的卡片上填上下列数的名称.你发现实数的分类示意图与这棵树枝干的形状有哪些联系吗?正有理数零负有理数正无理数负无理数有理数无理数实数活动2探究实数的分类(二)活动3 依据实数的分类(二)示意图,在右图的卡片上填上下列数的名称.你发现实数的分类示意图与这棵树枝干的形状有哪些联系吗? ①②实数③④⑤⑥⑦⑧正实数零负实数正有理数正无理数负有理数负无理数活动3判断下列说法是否正确,并说明理由: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?无理数 可以用数轴上的点来表示.A问题2.你能在数轴上表示出 吗?问题1.无理数能在数轴上表示出来吗?活动4- 每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。实数和数轴上的点是一一对应的.1.判断:(1)实数不是有理数就是无理数;( )(2)无理数都是无限不循环小数;( )(3)无理数都是无限小数; ( )(4)带根号的数都是无理数; ( )(5)无理数一定都带根号. ( )×× 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数.探索新知⑸│ - 1 │= 。⑴a是一个实数,它的相反数为 ;⑵如果a≠0,那么它的倒数为 ;⑶ a是一个正数,它的绝对值为 ;⑷ a是一个负数,它的绝对值为 ;-aa-a想一想-1(6)绝对值最小的实数是______02、填空:
(1) 的相反数是__________ (5) 绝对值是 _________ (2) 的倒数是____,(3)| |=___________(4)绝对值等于 的数是 _________ 的平方 是___ .(6)绝对值小于 的整数是___________★实数和数轴上的点是一一对应的. ★有序实数对和直角坐标系中的点是一 一对应的. 约公元600年,毕达哥拉斯学派认为宇宙万物
的总规律是服从整数化,认为世界上一切现象,都
能归结为整数或整数之比。正当毕氏学派津津乐道
地高唱“万物皆数”时,该学派的一位成员希伯索斯
利用推理的方法发现,正方形对角线与其一边之比
既不是整数,也不是分数。海神错判数学故事: 这个发现被当时的人们看成是“荒谬”和违反
常识的事。对于只有整数和整数比概念的他们来
说,这意味着正方形对角线与其一边之比竟然不
能用任何“数”来表示!这在数学史上称为第一次
数学危机。最后希伯索斯的发现没有被毕达哥拉
斯学派的信徒所接受,相传就因为这一发现,毕
达哥拉斯学派把希伯索斯投入大海中处死。海神错判数学故事:谢谢
