北师大版小学数学五年级下册第四单元 《长方体(二)—— 练习四》课件(共31张PPT)
文档属性
| 名称 | 北师大版小学数学五年级下册第四单元 《长方体(二)—— 练习四》课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 22:20:09 | ||
图片预览







文档简介
(共31张PPT)
练习四
北师大版五年级数学下册
第四单元 长方体(二)
体积的意义和体积单位:
物体所占空间的大小叫作物体的体积。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
重点回顾
容积的意义和容积单位:
容器所能容纳物体的体积叫作物体的容积。
计量容积要用容积单位,常用的容积单位有升和毫升,可以分别写成L和mL。
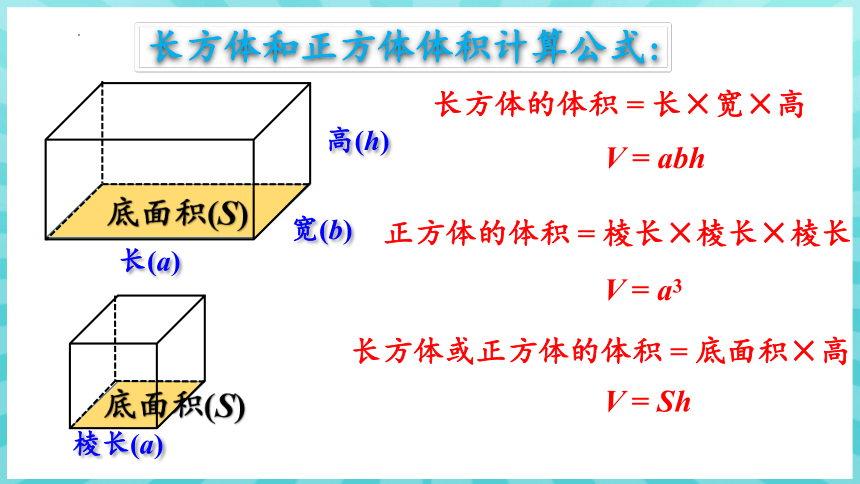
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
长方体或正方体的体积=底面积×高
V = Sh
宽(b)
长(a)
高(h)
底面积(S)
棱长(a)
底面积(S)
长方体和正方体体积计算公式:
单位间的进率:
1dm =1000cm
高级单位
低级单位
要乘进率,小数点向右移
要除以进率,小数点向左移
1m =1000dm
1L=1dm 1mL=1cm
1L=1000mL
看是不是相邻的体积单位,每相邻的两个体积单位间的进率是1000。
换算过程中“0”的个数要数清。
体积单位间的换算注意点:
要注意看清是由高级单位转化为低级单位,还是由低级单位转化为高级单位。
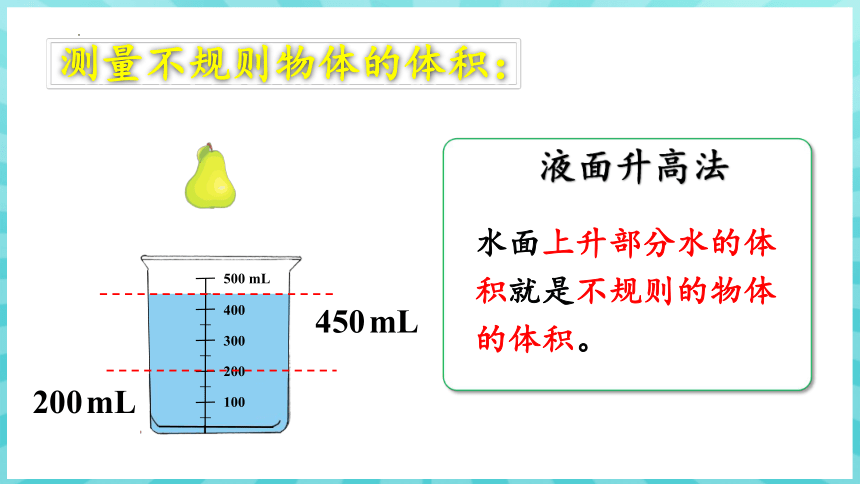
液面升高法
500 mL
400
300
200
100
200mL
450mL
水面上升部分水的体积就是不规则的物体的体积。
测量不规则物体的体积:
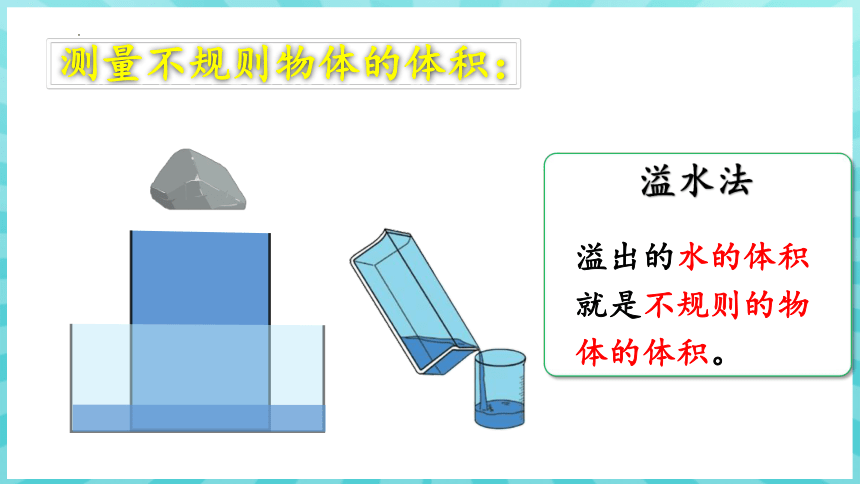
溢水法
溢出的水的体积就是不规则的物体的体积。
测量不规则物体的体积:
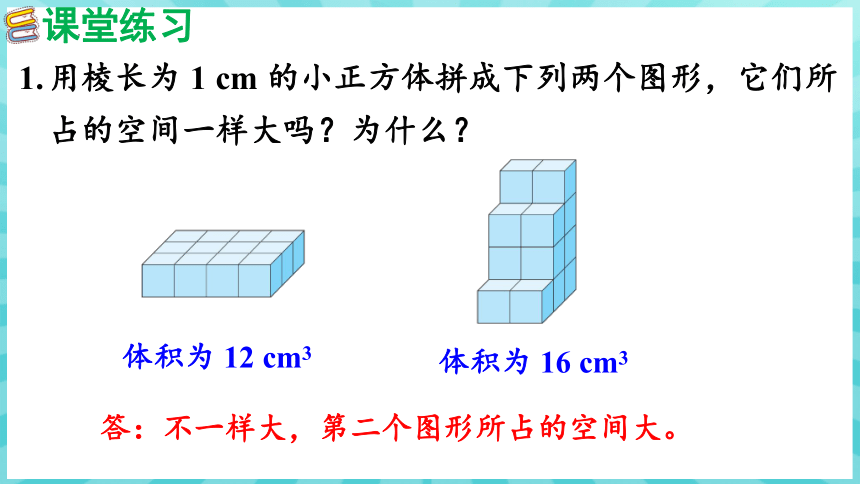
体积为 12 cm3
答:不一样大,第二个图形所占的空间大。
用棱长为 1 cm 的小正方体拼成下列两个图形,它们所占的空间一样大吗?为什么?
1.
体积为 16 cm3
填上适当的单位。
2.
一块橡皮的体积约是 10______。
一个文具盒的体积约是 0.35______。
一个词典的体积约是 900______。
一个讲台的体积约是 0.6_______。
dm3
cm3
cm3
m3
12×5×6
=60×6
=360(dm3)
9×9×9
=81×9
=729(cm3)
22×10×8
=220×8
=1760(cm3)
求出下列图形的体积。(单位:cm)
3.
一个长方体的长是12 cm,宽是长的 ,高是长的 ,
这个长方体的体积是多少?
4.
宽: 12× = 4 (cm)
12×4×3
= 48×3
= 144(cm3)
答:这个长方体的体积是 144 立方厘米。
高: 12× = 3 (cm)
0.35m3=( )dm3 2.04dm3=( )cm3
5300dm3=( )m3 2800cm3=( )dm3
19.6L=( )mL 1325mL=( )L
1m3=1000dm3
1L=1000mL
1dm3=1000cm3
350
2040
5.3
2.8
19600
1.325
5.
求下面两组数中,每一组都有一个数与其他数不同,请划去这个数。
6.
1 dm3 = 1000 cm3
1 m3 = 1000 dm3
3050000 cm3
3050000 cm3
7024 dm3
7024 dm3
70.24 dm3
一个棱长为 6 cm 的正方体药盒,它的表面积和体积分别是多少?
7.
6×6×6
=36×6
=216(cm2)
6×6×6
=36×6
=216(cm3)
表面积:
体积:
答:它的表面积是 216 cm2 ,体积是 216 cm3 。
表面积=一个面的面积×6
体积=棱长×棱长×棱长
6cm
一个长方体水箱的容积是 200 L,这个水箱的底面是一个边长为50 cm 的正方形,水箱的高是多少厘米?
8.
50×50=2500 (cm2)
200000÷2500=80(cm)
答:水箱的高是 80 厘米。
200 L=200 dm3 =200000 cm3
50cm
50cm
体积=底面积×高
高=体积÷底面积
在一块如右图的长方形地面上铺一层 6 cm 厚的沙土。(单位:m)
9.
长方体沙土的高
(1)需要多少立方米的沙土?
45
28
45×28×0.06=75.6(m3)
答:需要 75.6 立方米的沙土。
6 cm = 0.06 m
求体积
在一块如右图的长方形地面上铺一层 6 cm 厚的沙土。(单位:m)
9.
长方体沙土的高
45
28
(2)一辆车每次运送 1.5 m3 的沙土,
至少需要运多少次?
75.6 ÷1.5 = 50(次)……0.6(m )
还要再运一次
50 + 1 = 51(次)
答:至少需要运 51 次。
如图,一种旅行包的A、B、C三部分用拉链连接,拆卸方便。这种旅行包可以近似地看成是由右边的三个图形组成的,这个旅行包的容积大约是多少?(单位:cm)
10.
方法一
7×15×26=2730(cm3)
40×15×26=15600(cm3)
2730×2+15600=21060(cm3)
方法二
7+40+7=54(cm3)
54×15×26=21060(cm3)
答:这个旅行包的容积大约是 21060 cm3。
12×5=60(dm2) 12×2×2=48(dm2)
5×2×2=20(dm2)
60+48+20=128(dm2)
12×5×2=120(dm3) 120dm =120L
答:水槽最少需要128平方分米的铁皮,最多可以盛120升水。
做一个如右图的无盖长方体铁皮水槽最少需要多大面积的铁皮?这个水槽最多可以盛多少升水?(单位:dm)
11.
求表面积
求体积
12
5
2
某汽车油箱的长、宽、高如右图所示。(单位:cm)
12.
50×40×30=60000(cm3)
答:这个油箱能装60升汽油。
50
40
30
(1)这个油箱能装多少升汽油?
60000 cm3 =60000 mL=60 L
某汽车油箱的长、宽、高如右图所示。(单位:cm)
12.
50
40
30
(2)如果每升汽油可行驶 10 km,这箱油最多可以供这辆汽车行驶多少千米?
10×60=600(千米)
答:这箱油最多可以供这辆汽车行驶600千米。
不可以。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(1)用 4 个这样的小正方体可以摆成一个大正方体吗?
最少要用8个这样的小正方体。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(2)最少要用多少个这样的小正方体才可以摆成一个再大一点的正方体?
摆一个更大一点的正方体,用了27个这样的小正方体。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(3)你能再摆一个更大一点的正方体吗?用了多少个小正方体?
14.一辆卡车的长方体油箱从里面量长0.8 m、宽0.7 m、
高0.4 m,若每升汽油可使卡车行驶8.5 km,这辆卡车的油
箱装满油后可行驶多少千米?
1 m3=1000 L
0.8×0.7×0.4×1000×8.5=1904(km)
答:这辆卡车的油箱装满油后可行驶1904 km。
15.一个鱼缸从里面量长是50 cm,宽是25 cm,高是35 cm,
张扬向鱼缸中倒入37 L水,又放入一只螃蟹(完全浸没),
此时水面距鱼缸口还有5 cm,这只螃蟹的体积是多少?
37 L=37 dm3=37000 (cm3)
37000÷(50×25)=29.6(cm)
35-29.6-5=0.4(cm)
50×25×0.4=500(cm3)
答:这只螃蟹的体积是500 cm3。
16.一个正方形铁板的边长是60厘米,剪去四个相同的小正方形(如图所示),可以围成一个无盖的长方体铁盒。如果剪去的小正方形的边长是5厘米,围成的长方体铁盒的容积是多少毫升?(铁板的厚度忽略不计)
(60-5×2)×(60-5×2)×5=12500(立方厘米)
12500立方厘米=12500毫升
答:围成的长方体铁盒的容积是12500毫升。
1.有一个棱长是40 cm的正方体容器和一个长60 cm、宽40
cm、高40 cm的长方体容器,长方体容器中装有28 cm深的水。
如果将长方体容器中的水倒一部分到正方体容器中,使两个容
器中的水面同样高,这时两个容器中的水面高度是多少?
60×40×28=67200(cm3)
67200÷(60+40)÷40=16.8(cm)
答:这时两个容器中的水面高度是16.8 cm。
拓展提升
2.在一个棱长为5 cm的大正方体的六个面的中心分别粘上一个
棱长为2 cm的小正方体(如图),组成的几何体的表面积和体
积分别是多少?
表面积:5×5×6=150(cm2)
2×2×4×6=96(cm2)
150+96=246(cm2)
体积:5×5×5=125(cm3)
2×2×2×6=48(cm3)
125+48=173(cm3)
答:组成的几何体的表面积是246 cm2,体积是173 cm3。
练习四
北师大版五年级数学下册
第四单元 长方体(二)
体积的意义和体积单位:
物体所占空间的大小叫作物体的体积。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
重点回顾
容积的意义和容积单位:
容器所能容纳物体的体积叫作物体的容积。
计量容积要用容积单位,常用的容积单位有升和毫升,可以分别写成L和mL。
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
长方体或正方体的体积=底面积×高
V = Sh
宽(b)
长(a)
高(h)
底面积(S)
棱长(a)
底面积(S)
长方体和正方体体积计算公式:
单位间的进率:
1dm =1000cm
高级单位
低级单位
要乘进率,小数点向右移
要除以进率,小数点向左移
1m =1000dm
1L=1dm 1mL=1cm
1L=1000mL
看是不是相邻的体积单位,每相邻的两个体积单位间的进率是1000。
换算过程中“0”的个数要数清。
体积单位间的换算注意点:
要注意看清是由高级单位转化为低级单位,还是由低级单位转化为高级单位。
液面升高法
500 mL
400
300
200
100
200mL
450mL
水面上升部分水的体积就是不规则的物体的体积。
测量不规则物体的体积:
溢水法
溢出的水的体积就是不规则的物体的体积。
测量不规则物体的体积:
体积为 12 cm3
答:不一样大,第二个图形所占的空间大。
用棱长为 1 cm 的小正方体拼成下列两个图形,它们所占的空间一样大吗?为什么?
1.
体积为 16 cm3
填上适当的单位。
2.
一块橡皮的体积约是 10______。
一个文具盒的体积约是 0.35______。
一个词典的体积约是 900______。
一个讲台的体积约是 0.6_______。
dm3
cm3
cm3
m3
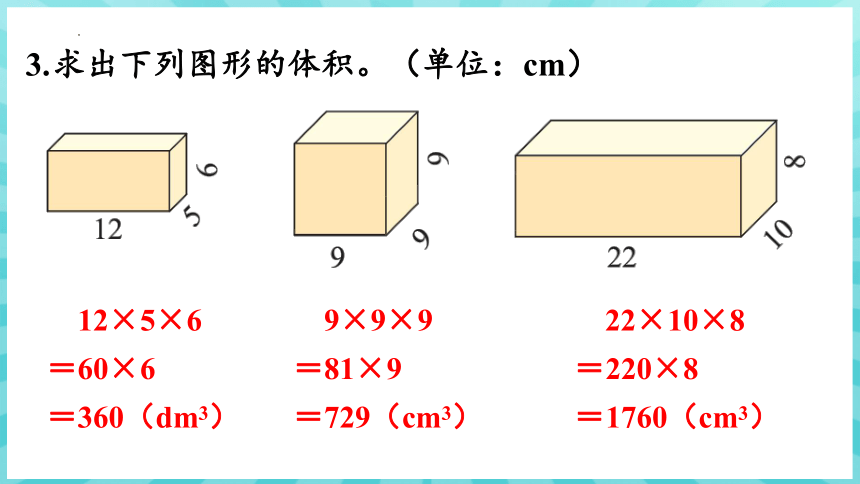
12×5×6
=60×6
=360(dm3)
9×9×9
=81×9
=729(cm3)
22×10×8
=220×8
=1760(cm3)
求出下列图形的体积。(单位:cm)
3.
一个长方体的长是12 cm,宽是长的 ,高是长的 ,
这个长方体的体积是多少?
4.
宽: 12× = 4 (cm)
12×4×3
= 48×3
= 144(cm3)
答:这个长方体的体积是 144 立方厘米。
高: 12× = 3 (cm)
0.35m3=( )dm3 2.04dm3=( )cm3
5300dm3=( )m3 2800cm3=( )dm3
19.6L=( )mL 1325mL=( )L
1m3=1000dm3
1L=1000mL
1dm3=1000cm3
350
2040
5.3
2.8
19600
1.325
5.
求下面两组数中,每一组都有一个数与其他数不同,请划去这个数。
6.
1 dm3 = 1000 cm3
1 m3 = 1000 dm3
3050000 cm3
3050000 cm3
7024 dm3
7024 dm3
70.24 dm3
一个棱长为 6 cm 的正方体药盒,它的表面积和体积分别是多少?
7.
6×6×6
=36×6
=216(cm2)
6×6×6
=36×6
=216(cm3)
表面积:
体积:
答:它的表面积是 216 cm2 ,体积是 216 cm3 。
表面积=一个面的面积×6
体积=棱长×棱长×棱长
6cm
一个长方体水箱的容积是 200 L,这个水箱的底面是一个边长为50 cm 的正方形,水箱的高是多少厘米?
8.
50×50=2500 (cm2)
200000÷2500=80(cm)
答:水箱的高是 80 厘米。
200 L=200 dm3 =200000 cm3
50cm
50cm
体积=底面积×高
高=体积÷底面积
在一块如右图的长方形地面上铺一层 6 cm 厚的沙土。(单位:m)
9.
长方体沙土的高
(1)需要多少立方米的沙土?
45
28
45×28×0.06=75.6(m3)
答:需要 75.6 立方米的沙土。
6 cm = 0.06 m
求体积
在一块如右图的长方形地面上铺一层 6 cm 厚的沙土。(单位:m)
9.
长方体沙土的高
45
28
(2)一辆车每次运送 1.5 m3 的沙土,
至少需要运多少次?
75.6 ÷1.5 = 50(次)……0.6(m )
还要再运一次
50 + 1 = 51(次)
答:至少需要运 51 次。
如图,一种旅行包的A、B、C三部分用拉链连接,拆卸方便。这种旅行包可以近似地看成是由右边的三个图形组成的,这个旅行包的容积大约是多少?(单位:cm)
10.
方法一
7×15×26=2730(cm3)
40×15×26=15600(cm3)
2730×2+15600=21060(cm3)
方法二
7+40+7=54(cm3)
54×15×26=21060(cm3)
答:这个旅行包的容积大约是 21060 cm3。
12×5=60(dm2) 12×2×2=48(dm2)
5×2×2=20(dm2)
60+48+20=128(dm2)
12×5×2=120(dm3) 120dm =120L
答:水槽最少需要128平方分米的铁皮,最多可以盛120升水。
做一个如右图的无盖长方体铁皮水槽最少需要多大面积的铁皮?这个水槽最多可以盛多少升水?(单位:dm)
11.
求表面积
求体积
12
5
2
某汽车油箱的长、宽、高如右图所示。(单位:cm)
12.
50×40×30=60000(cm3)
答:这个油箱能装60升汽油。
50
40
30
(1)这个油箱能装多少升汽油?
60000 cm3 =60000 mL=60 L
某汽车油箱的长、宽、高如右图所示。(单位:cm)
12.
50
40
30
(2)如果每升汽油可行驶 10 km,这箱油最多可以供这辆汽车行驶多少千米?
10×60=600(千米)
答:这箱油最多可以供这辆汽车行驶600千米。
不可以。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(1)用 4 个这样的小正方体可以摆成一个大正方体吗?
最少要用8个这样的小正方体。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(2)最少要用多少个这样的小正方体才可以摆成一个再大一点的正方体?
摆一个更大一点的正方体,用了27个这样的小正方体。
实践活动。找一些棱长为 1 cm 的小正方体,做下面的活动。
13.
(3)你能再摆一个更大一点的正方体吗?用了多少个小正方体?
14.一辆卡车的长方体油箱从里面量长0.8 m、宽0.7 m、
高0.4 m,若每升汽油可使卡车行驶8.5 km,这辆卡车的油
箱装满油后可行驶多少千米?
1 m3=1000 L
0.8×0.7×0.4×1000×8.5=1904(km)
答:这辆卡车的油箱装满油后可行驶1904 km。
15.一个鱼缸从里面量长是50 cm,宽是25 cm,高是35 cm,
张扬向鱼缸中倒入37 L水,又放入一只螃蟹(完全浸没),
此时水面距鱼缸口还有5 cm,这只螃蟹的体积是多少?
37 L=37 dm3=37000 (cm3)
37000÷(50×25)=29.6(cm)
35-29.6-5=0.4(cm)
50×25×0.4=500(cm3)
答:这只螃蟹的体积是500 cm3。
16.一个正方形铁板的边长是60厘米,剪去四个相同的小正方形(如图所示),可以围成一个无盖的长方体铁盒。如果剪去的小正方形的边长是5厘米,围成的长方体铁盒的容积是多少毫升?(铁板的厚度忽略不计)
(60-5×2)×(60-5×2)×5=12500(立方厘米)
12500立方厘米=12500毫升
答:围成的长方体铁盒的容积是12500毫升。
1.有一个棱长是40 cm的正方体容器和一个长60 cm、宽40
cm、高40 cm的长方体容器,长方体容器中装有28 cm深的水。
如果将长方体容器中的水倒一部分到正方体容器中,使两个容
器中的水面同样高,这时两个容器中的水面高度是多少?
60×40×28=67200(cm3)
67200÷(60+40)÷40=16.8(cm)
答:这时两个容器中的水面高度是16.8 cm。
拓展提升
2.在一个棱长为5 cm的大正方体的六个面的中心分别粘上一个
棱长为2 cm的小正方体(如图),组成的几何体的表面积和体
积分别是多少?
表面积:5×5×6=150(cm2)
2×2×4×6=96(cm2)
150+96=246(cm2)
体积:5×5×5=125(cm3)
2×2×2×6=48(cm3)
125+48=173(cm3)
答:组成的几何体的表面积是246 cm2,体积是173 cm3。
