北师大版小学数学五年级下册4.1 《体积与容积》课件(共27张PPT)
文档属性
| 名称 | 北师大版小学数学五年级下册4.1 《体积与容积》课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
体积与容积
北师大版五年级数学下册
第四单元 长方体(二)
通过具体的实验活动,了解体积与容积的实际含义,初步理解体积和容积的概念。
在操作交流中,引导学生掌握在不同环境中比较体积大小的多种方法,感受物体体积的大小,发展空间观念。
学习目标
乌鸦是怎样喝到水的?为什么?
通过接下来的学习我们就知道乌鸦喝水的原理啦!
乌鸦喝水
教室里哪些物品占的空间大?哪些物品占的空间小?
课桌占的空间大,粉笔盒占的空间小。
常见的容器中,哪些容器放的东西多?哪些容器放的东西少?
水桶盛的东西多,水杯盛的东西少。
土豆和红薯哪一个占的空间大呢?想一想,做一做。
大小比较接近,用眼睛难以判断。
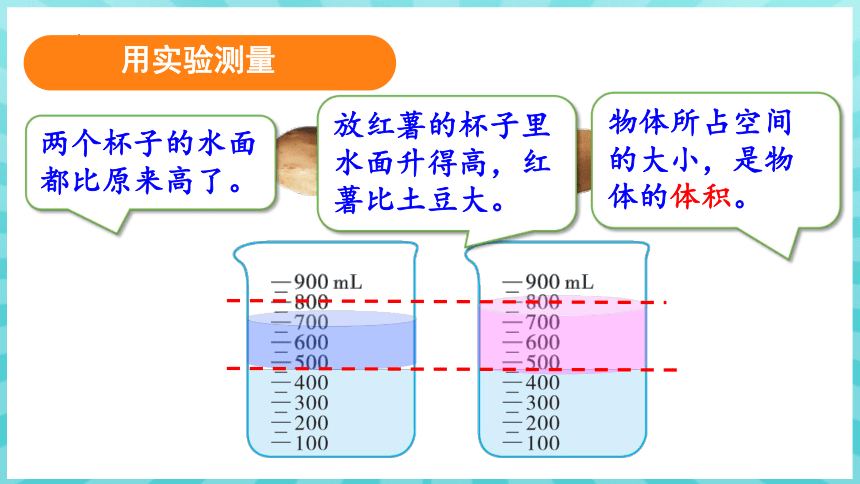
用实验测量
两个杯子的水面都比原来高了。
放红薯的杯子里水面升得高,红薯比土豆大。
物体所占空间的大小,是物体的体积。
两个杯子中哪一个装水多呢?请你设计一个实验解决这个问题。
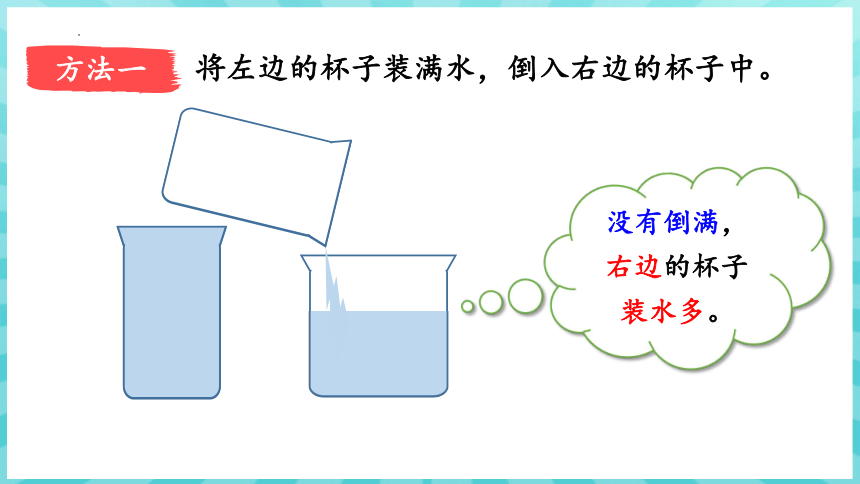
方法一
将左边的杯子装满水,倒入右边的杯子中。
没有倒满,右边的杯子装水多。
方法一
将左边的杯子装满水,倒入右边的杯子中。
正好倒满,两个杯子装水一样多。
方法一
将左边的杯子装满水,倒入右边的杯子中。
还有剩余,左边的杯子装水多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
左边的杯子装水多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
两个杯子装水一样多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
右边的杯子装水多。
认识容积
体积与容积的区别
所有的物体都有体积,不是所有的物体都有容积。
只有容器才有容积。
有体积,没有容积
有体积,有容积
体积与容积的区别
体积是从外部测量的,容积是从内部测量的。
当容器壁较薄,可以忽略不计时,体积等于容积。
一般情况下,同一个物体的体积比容积大。
橡皮泥
一团橡皮泥,淘气第一次把它捏成长方体,第二次把它捏成球。捏成的两个物体哪一个体积大?为什么?
1.
一样大。
无论形状怎么变,都是用同一团橡皮泥做的。
一用相同数量的硬币分别垒成下面的形状,哪一个体积大?为什么?
2.
1元硬币
1角硬币
1元硬币
第一堆和第三堆的体积最大,且一样大。
1元硬币的体积比1角硬币的体积大。
10枚
10枚
10枚
淘气和笑笑各有一瓶同样多的饮料,淘气倒了 3 杯,而笑笑只倒了 2 杯,你认为有可能吗?说一说你的想法。
3.
淘气的杯子
笑笑的杯子
我认为有可能。
如果每个杯子的大小不同,那么淘气的 3 杯就可能等于笑笑的 2 杯。
淘气的杯子小,笑笑的杯子大。
一行有3个
一层有 (3×4) 个小正方体
数一数,想一想,再与同伴说一说,右图中的长方体
盒子能装多少个这样的小正方体?
4.
一层有4行
有3层
一共能装 (3×4×3) 个小正方体
一行有3个
数一数,想一想,再与同伴说一说,右图中的长方体
盒子能装多少个这样的小正方体?
4.
一层有4行
有3层
答:这个长方体盒子能装36个
这样的小正方体。
3×4×3 = 36(个)
谁搭的长方体体积大?
5.
5
2
3
5×2×3 = 30(个)
6
2
2
6×2×2 = 24(个)
答: 笑笑搭的长方体体积大。
6
2
1
3
2
2
用 12 个大小相同的小正方体,分别按下面的要求想一想,搭一搭。
6.
(1)搭出两个物体,使它们的体积相同。
小正方体的个数相同。
2
2
2
2
2
用 12 个大小相同的小正方体,分别按下面的要求想一想,搭一搭。
6.
(2)搭出两个物体,使其中一个物体的体积是另一个的 2 倍。
其中一个小正方体的个数是另一个的2倍。
下面图片都是由同样大小的正方体拼成的,将这些图形按表
面积从大到小排序:( ③>②>⑤>①>④ );按体积
从小到大排序:( ④<①<⑤<②<③ )。
①
②
③
④
⑤
③>②>⑤>①>④
④<①<⑤<②<③
拓展提升
这节课你有什么收获?
物体所占空间的大小,叫做物体的体积。
容器所能容纳物体的体积,是容器的容积。
课堂小结
体积与容积
北师大版五年级数学下册
第四单元 长方体(二)
通过具体的实验活动,了解体积与容积的实际含义,初步理解体积和容积的概念。
在操作交流中,引导学生掌握在不同环境中比较体积大小的多种方法,感受物体体积的大小,发展空间观念。
学习目标
乌鸦是怎样喝到水的?为什么?
通过接下来的学习我们就知道乌鸦喝水的原理啦!
乌鸦喝水
教室里哪些物品占的空间大?哪些物品占的空间小?
课桌占的空间大,粉笔盒占的空间小。
常见的容器中,哪些容器放的东西多?哪些容器放的东西少?
水桶盛的东西多,水杯盛的东西少。
土豆和红薯哪一个占的空间大呢?想一想,做一做。
大小比较接近,用眼睛难以判断。
用实验测量
两个杯子的水面都比原来高了。
放红薯的杯子里水面升得高,红薯比土豆大。
物体所占空间的大小,是物体的体积。
两个杯子中哪一个装水多呢?请你设计一个实验解决这个问题。
方法一
将左边的杯子装满水,倒入右边的杯子中。
没有倒满,右边的杯子装水多。
方法一
将左边的杯子装满水,倒入右边的杯子中。
正好倒满,两个杯子装水一样多。
方法一
将左边的杯子装满水,倒入右边的杯子中。
还有剩余,左边的杯子装水多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
左边的杯子装水多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
两个杯子装水一样多。
方法二
将两个杯子都装满水,分别倒入相同的小杯子中。
右边的杯子装水多。
认识容积
体积与容积的区别
所有的物体都有体积,不是所有的物体都有容积。
只有容器才有容积。
有体积,没有容积
有体积,有容积
体积与容积的区别
体积是从外部测量的,容积是从内部测量的。
当容器壁较薄,可以忽略不计时,体积等于容积。
一般情况下,同一个物体的体积比容积大。
橡皮泥
一团橡皮泥,淘气第一次把它捏成长方体,第二次把它捏成球。捏成的两个物体哪一个体积大?为什么?
1.
一样大。
无论形状怎么变,都是用同一团橡皮泥做的。
一用相同数量的硬币分别垒成下面的形状,哪一个体积大?为什么?
2.
1元硬币
1角硬币
1元硬币
第一堆和第三堆的体积最大,且一样大。
1元硬币的体积比1角硬币的体积大。
10枚
10枚
10枚
淘气和笑笑各有一瓶同样多的饮料,淘气倒了 3 杯,而笑笑只倒了 2 杯,你认为有可能吗?说一说你的想法。
3.
淘气的杯子
笑笑的杯子
我认为有可能。
如果每个杯子的大小不同,那么淘气的 3 杯就可能等于笑笑的 2 杯。
淘气的杯子小,笑笑的杯子大。
一行有3个
一层有 (3×4) 个小正方体
数一数,想一想,再与同伴说一说,右图中的长方体
盒子能装多少个这样的小正方体?
4.
一层有4行
有3层
一共能装 (3×4×3) 个小正方体
一行有3个
数一数,想一想,再与同伴说一说,右图中的长方体
盒子能装多少个这样的小正方体?
4.
一层有4行
有3层
答:这个长方体盒子能装36个
这样的小正方体。
3×4×3 = 36(个)
谁搭的长方体体积大?
5.
5
2
3
5×2×3 = 30(个)
6
2
2
6×2×2 = 24(个)
答: 笑笑搭的长方体体积大。
6
2
1
3
2
2
用 12 个大小相同的小正方体,分别按下面的要求想一想,搭一搭。
6.
(1)搭出两个物体,使它们的体积相同。
小正方体的个数相同。
2
2
2
2
2
用 12 个大小相同的小正方体,分别按下面的要求想一想,搭一搭。
6.
(2)搭出两个物体,使其中一个物体的体积是另一个的 2 倍。
其中一个小正方体的个数是另一个的2倍。
下面图片都是由同样大小的正方体拼成的,将这些图形按表
面积从大到小排序:( ③>②>⑤>①>④ );按体积
从小到大排序:( ④<①<⑤<②<③ )。
①
②
③
④
⑤
③>②>⑤>①>④
④<①<⑤<②<③
拓展提升
这节课你有什么收获?
物体所占空间的大小,叫做物体的体积。
容器所能容纳物体的体积,是容器的容积。
课堂小结
