北师大版小学数学五年级下册8.4 《平均数的再认识》课件(共22张ppt)
文档属性
| 名称 | 北师大版小学数学五年级下册8.4 《平均数的再认识》课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 22:46:45 | ||
图片预览







文档简介
平均数的再认识
北师版数学五年级(下)
八 数据的表示和分析
结合生活实际,在进一步理解平均数的意义的基础上,掌握求平均数的方法。
能运用平均数解决简单的实际问题,体会平均数在实际生活中的应用。。
在探索知识的过程中,增强学好数学的信心,提高自主学习的能力。
你还记得平均数吗?
中国男子篮球队平均身高是200厘米(2米)。
一组数据的总和除以这组数据的个数所得的商,称为这组数据的平均数。
你坐公交车的时候测量过身高吗?
从2022 年9 月1 日起,武汉市把儿童乘坐城市公共交通工具的免票线从 1.2 m 调整到 1.3 m。
(1)用自己的语言说一说,为什么要把免票线调整到1.3 m?
现在生活条件好了,儿童的身高也高了。
被调查的儿童的平均身高可能高了。
从2022 年9 月1 日起,武汉市把儿童乘坐城市公共交通工具的免票线从 1.2 m 调整到 1.3 m。
(2)据调查,武汉市某校 6 岁男童的身高平均值为 126.5 cm,
女童的身高平均值为 124.0 cm。请根据上面信息解释
免票线调整的合理性。
126.5 cm
124.0 cm
这两个平均值都小于并接近 1.3 m,所以免票线从 1.2 m 调整到 1.3 m 是合理的。
平均数不是一个孤立的数据,它是反映数据集中趋势的一项指标,具有代表性。
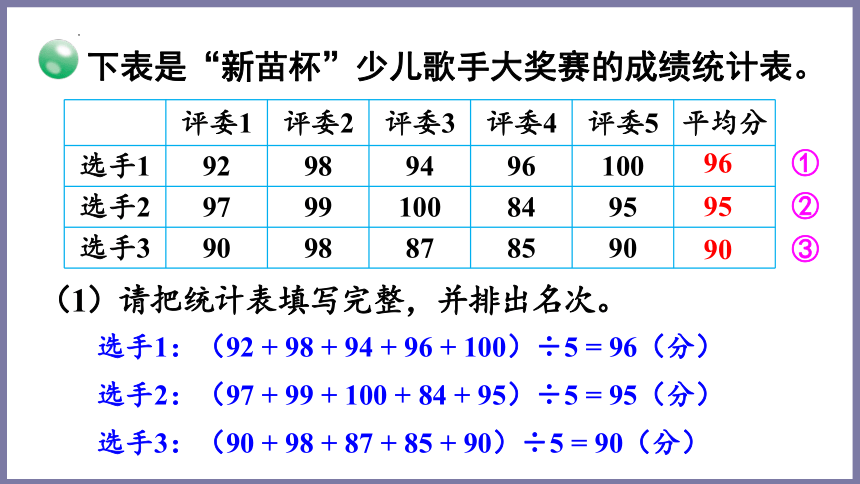
下表是“新苗杯”少儿歌手大奖赛的成绩统计表。
评委1
评委2
评委3
评委4
评委5
平均分
选手1
92
98
94
96
100
选手2
97
99
100
84
95
选手3
90
98
87
85
90
(1)请把统计表填写完整,并排出名次。
选手1:(92 + 98 + 94 + 96 + 100)÷5 = 96(分)
选手2:(97 + 99 + 100 + 84 + 95)÷5 = 95(分)
选手3:(90 + 98 + 87 + 85 + 90)÷5 = 90(分)
96
95
90
①
②
③
(2)在实际比赛中,通常都采取去掉一个最高分和一个
最低分,然后再计算平均分的记分方法,你能说出
其中的道理吗?
有的评委打分太高或太低。
去掉后再求平均就更具代表性了。
评委1
评委2
评委3
评委4
评委5
平均分
选手1
92
98
94
96
100
选手2
97
99
100
84
95
选手3
90
98
87
85
90
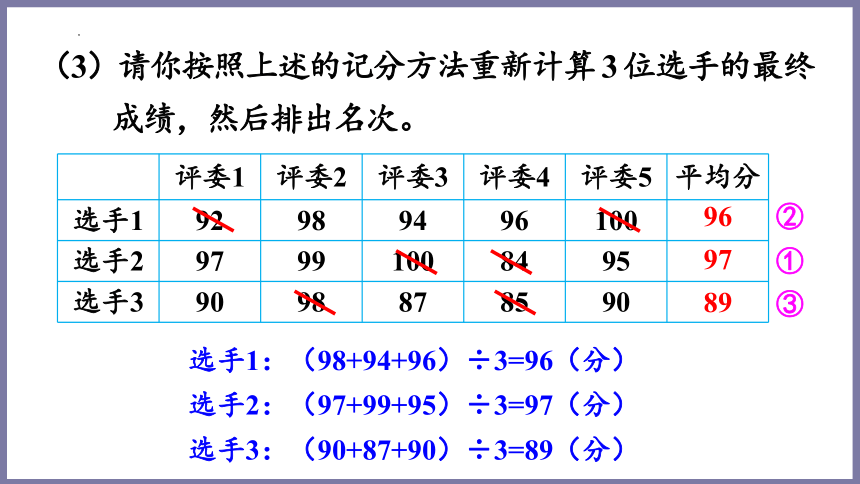
(3)请你按照上述的记分方法重新计算 3 位选手的最终
成绩,然后排出名次。
选手1:(98+94+96)÷3=96(分)
选手2:(97+99+95)÷3=97(分)
选手3:(90+87+90)÷3=89(分)
96
97
89
①
②
③
说一说,你对平均数有了哪些新的认识
平均数具有代表性,能帮助我们解决问题。
任何一个数有变化,平均数都有反应。平均数真的很灵敏。
(1)分别计算这个组对数学和英语喜欢程度的平均分。
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是
他们展开了调查。下面是他们调查时使用的评分标准。
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
学生9
学生10
合计
数学
1
4
5
2
4
3
2
1
5
3
30
英语
2
4
4
2
2
3
1
1
3
2
24
数学:30÷10=3(分) 英语:24÷10=2.4(分)
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是
他们展开了调查。下面是他们调查时使用的评分标准。
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
学生9
学生10
合计
数学
1
4
5
2
4
3
2
1
5
3
30
英语
2
4
4
2
2
3
1
1
3
2
24
数学更受欢迎。
淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
2.
(1)计算这些小朋友的平均年龄。
(7+7+7+8+8+8+9+9)÷8
=63÷8
=7.875(岁)
答:这些小朋友的平均年龄是7.875岁。
淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
2.
(2)这时,老师也加入做游戏的队伍。他的年龄是 45 岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(63+45)÷9=12(岁)
答:此时做游戏的人的平均年龄是12岁。对于这一组数据,45是个极端数据,对平均年龄影响较大。
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
根据上面的结果,将 8 种水果按照喜好程度从高到低排序,并说明排序的理由。
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
苹果得分是6
香蕉得分是9
西瓜得分是12
橘子得分是17
葡萄得分是19
梨得分是25
桃得分是28
菠萝得分是28
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
按喜好程度从高到低排序:
苹果、香蕉、西瓜、橘子、葡萄、梨、桃和菠萝。
理由:得分越低,喜欢程度越高。
下面水池的平均水深是110 cm。
4.
会有危险,虽然平均水深是110cm,但有的地方会深,有的地方会浅一些,深处可能超过140cm!
我身高140cm,下水游泳会不会有危险?
5.随着信息技术的高速发展,电商平台也得到越来越多人的
青睐。下面是在某电商平台上,五位顾客对两家店铺的评分
(一颗星表示一分):
{5940675A-B579-460E-94D1-54222C63F5DA}
顾客1
顾客2
顾客3
顾客4
顾客5
甲店
☆☆
☆☆
☆☆
☆☆
☆☆☆
☆☆
☆☆
☆☆☆
乙店
☆☆
☆☆☆
☆☆☆
☆☆
☆☆☆
☆☆
☆☆
(1)请根据这五位顾客的评分,分别计算出甲店和乙店的平均分。
(2)假如你要去这两家店铺购买商品,你会选择哪一家?请说明理由。
(1)请根据这五位顾客的评分,分别计算出甲店和乙店的平
均分。
甲店:(4+4+3+4+3)÷5=3.6(分)
乙店:(5+3+2+3+4)÷5=3.4(分)
答:甲店的平均分为3.6分,乙店的平均分为3.4分。
(2)假如你要去这两家店铺购买商品,你会选择哪一家?请
说明理由。
(答案不唯一)我会选择甲店,因为甲店的平均分更
高。
有5名裁判给一名运动员进行评分,去掉一个最高分后平均分是9.46分,去掉一个最低分后平均分是9.66分,这个运动员的最高分和最低分相差多少?
9.66×4-9.46×4=0.8(分)
答:这个运动员的最高分和最低分相差0.8分。
拓展提升
这节课你有什么收获?
1.平均数的意义:
一组数据中所有数据之和除以数据的个数。
2.平均数具有代表性:
它能反映一组数据的集中趋势。
3.平均数具有灵敏性:易受极端数据的影响,数据过大或过小都会影响到最终结果。
北师版数学五年级(下)
八 数据的表示和分析
结合生活实际,在进一步理解平均数的意义的基础上,掌握求平均数的方法。
能运用平均数解决简单的实际问题,体会平均数在实际生活中的应用。。
在探索知识的过程中,增强学好数学的信心,提高自主学习的能力。
你还记得平均数吗?
中国男子篮球队平均身高是200厘米(2米)。
一组数据的总和除以这组数据的个数所得的商,称为这组数据的平均数。
你坐公交车的时候测量过身高吗?
从2022 年9 月1 日起,武汉市把儿童乘坐城市公共交通工具的免票线从 1.2 m 调整到 1.3 m。
(1)用自己的语言说一说,为什么要把免票线调整到1.3 m?
现在生活条件好了,儿童的身高也高了。
被调查的儿童的平均身高可能高了。
从2022 年9 月1 日起,武汉市把儿童乘坐城市公共交通工具的免票线从 1.2 m 调整到 1.3 m。
(2)据调查,武汉市某校 6 岁男童的身高平均值为 126.5 cm,
女童的身高平均值为 124.0 cm。请根据上面信息解释
免票线调整的合理性。
126.5 cm
124.0 cm
这两个平均值都小于并接近 1.3 m,所以免票线从 1.2 m 调整到 1.3 m 是合理的。
平均数不是一个孤立的数据,它是反映数据集中趋势的一项指标,具有代表性。
下表是“新苗杯”少儿歌手大奖赛的成绩统计表。
评委1
评委2
评委3
评委4
评委5
平均分
选手1
92
98
94
96
100
选手2
97
99
100
84
95
选手3
90
98
87
85
90
(1)请把统计表填写完整,并排出名次。
选手1:(92 + 98 + 94 + 96 + 100)÷5 = 96(分)
选手2:(97 + 99 + 100 + 84 + 95)÷5 = 95(分)
选手3:(90 + 98 + 87 + 85 + 90)÷5 = 90(分)
96
95
90
①
②
③
(2)在实际比赛中,通常都采取去掉一个最高分和一个
最低分,然后再计算平均分的记分方法,你能说出
其中的道理吗?
有的评委打分太高或太低。
去掉后再求平均就更具代表性了。
评委1
评委2
评委3
评委4
评委5
平均分
选手1
92
98
94
96
100
选手2
97
99
100
84
95
选手3
90
98
87
85
90
(3)请你按照上述的记分方法重新计算 3 位选手的最终
成绩,然后排出名次。
选手1:(98+94+96)÷3=96(分)
选手2:(97+99+95)÷3=97(分)
选手3:(90+87+90)÷3=89(分)
96
97
89
①
②
③
说一说,你对平均数有了哪些新的认识
平均数具有代表性,能帮助我们解决问题。
任何一个数有变化,平均数都有反应。平均数真的很灵敏。
(1)分别计算这个组对数学和英语喜欢程度的平均分。
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是
他们展开了调查。下面是他们调查时使用的评分标准。
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
学生9
学生10
合计
数学
1
4
5
2
4
3
2
1
5
3
30
英语
2
4
4
2
2
3
1
1
3
2
24
数学:30÷10=3(分) 英语:24÷10=2.4(分)
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是
他们展开了调查。下面是他们调查时使用的评分标准。
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
学生9
学生10
合计
数学
1
4
5
2
4
3
2
1
5
3
30
英语
2
4
4
2
2
3
1
1
3
2
24
数学更受欢迎。
淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
2.
(1)计算这些小朋友的平均年龄。
(7+7+7+8+8+8+9+9)÷8
=63÷8
=7.875(岁)
答:这些小朋友的平均年龄是7.875岁。
淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
2.
(2)这时,老师也加入做游戏的队伍。他的年龄是 45 岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(63+45)÷9=12(岁)
答:此时做游戏的人的平均年龄是12岁。对于这一组数据,45是个极端数据,对平均年龄影响较大。
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
根据上面的结果,将 8 种水果按照喜好程度从高到低排序,并说明排序的理由。
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
苹果得分是6
香蕉得分是9
西瓜得分是12
橘子得分是17
葡萄得分是19
梨得分是25
桃得分是28
菠萝得分是28
下面是某班 4 个小组学生对 8 种水果(香蕉、苹果、梨、桃、橘子、西瓜、葡萄、菠萝)喜好程度的排序结果,1 表示喜好程度最高。
3.
按喜好程度从高到低排序:
苹果、香蕉、西瓜、橘子、葡萄、梨、桃和菠萝。
理由:得分越低,喜欢程度越高。
下面水池的平均水深是110 cm。
4.
会有危险,虽然平均水深是110cm,但有的地方会深,有的地方会浅一些,深处可能超过140cm!
我身高140cm,下水游泳会不会有危险?
5.随着信息技术的高速发展,电商平台也得到越来越多人的
青睐。下面是在某电商平台上,五位顾客对两家店铺的评分
(一颗星表示一分):
{5940675A-B579-460E-94D1-54222C63F5DA}
顾客1
顾客2
顾客3
顾客4
顾客5
甲店
☆☆
☆☆
☆☆
☆☆
☆☆☆
☆☆
☆☆
☆☆☆
乙店
☆☆
☆☆☆
☆☆☆
☆☆
☆☆☆
☆☆
☆☆
(1)请根据这五位顾客的评分,分别计算出甲店和乙店的平均分。
(2)假如你要去这两家店铺购买商品,你会选择哪一家?请说明理由。
(1)请根据这五位顾客的评分,分别计算出甲店和乙店的平
均分。
甲店:(4+4+3+4+3)÷5=3.6(分)
乙店:(5+3+2+3+4)÷5=3.4(分)
答:甲店的平均分为3.6分,乙店的平均分为3.4分。
(2)假如你要去这两家店铺购买商品,你会选择哪一家?请
说明理由。
(答案不唯一)我会选择甲店,因为甲店的平均分更
高。
有5名裁判给一名运动员进行评分,去掉一个最高分后平均分是9.46分,去掉一个最低分后平均分是9.66分,这个运动员的最高分和最低分相差多少?
9.66×4-9.46×4=0.8(分)
答:这个运动员的最高分和最低分相差0.8分。
拓展提升
这节课你有什么收获?
1.平均数的意义:
一组数据中所有数据之和除以数据的个数。
2.平均数具有代表性:
它能反映一组数据的集中趋势。
3.平均数具有灵敏性:易受极端数据的影响,数据过大或过小都会影响到最终结果。
