北师大版五年级下册数学4.5 长方体的体积(2)(课件)(共18张PPT)
文档属性
| 名称 | 北师大版五年级下册数学4.5 长方体的体积(2)(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
长方体的体积(2)
北师大版五年级数学下册
第四单元 长方体(二)
经历长方体和正方体统一的体积计算公式的推导过程,进一步认识两种几何体的基本特征及它们之间的关系。
理解底面积的基础上掌握长方体和正方体统一的体积计算公式,会应用长方体和正方体统一的体积计算公式解决一些简单的实际问题。
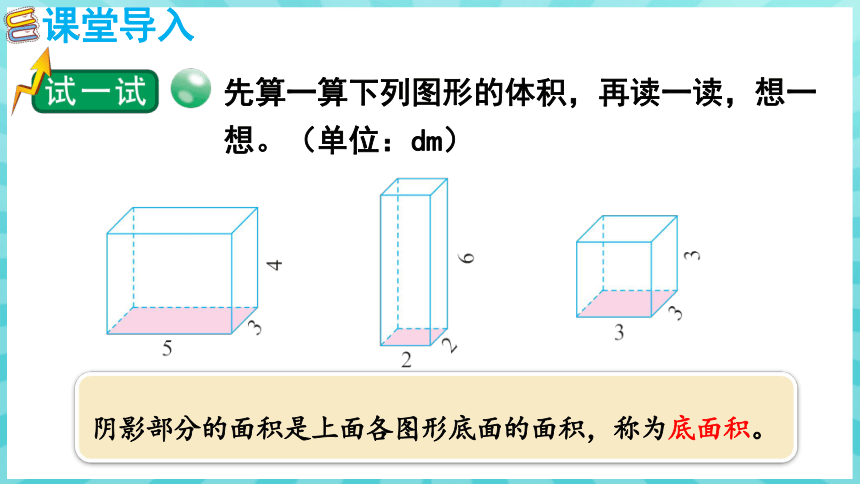
5×3×4
=15×4
=60 (dm3)
2×2×6
=4×6
=24 (dm3)
3×3×3
=9×3
=27 (dm3)
阴影部分的面积是上面各图形底面的面积,称为底面积。
先算一算下列图形的体积,再读一读,想一想。(单位:dm)
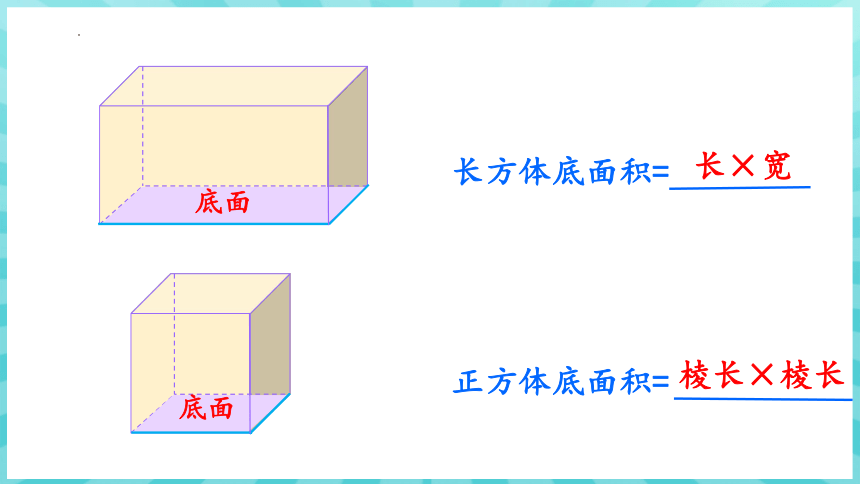
底面
底面
长方体底面积=
长×宽
正方体底面积=
棱长×棱长
底面
底面
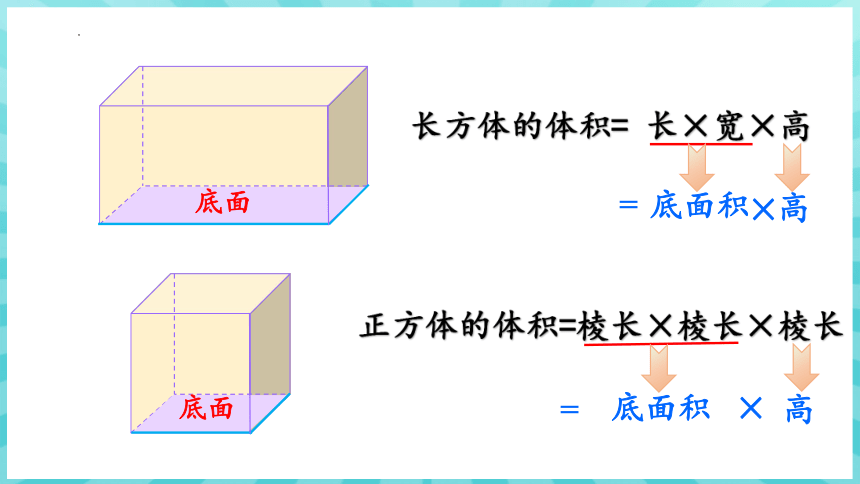
长方体的体积= 长×宽×高
底面积
高
×
正方体的体积=棱长×棱长×棱长
底面积
=
高
×
=
底面
底面
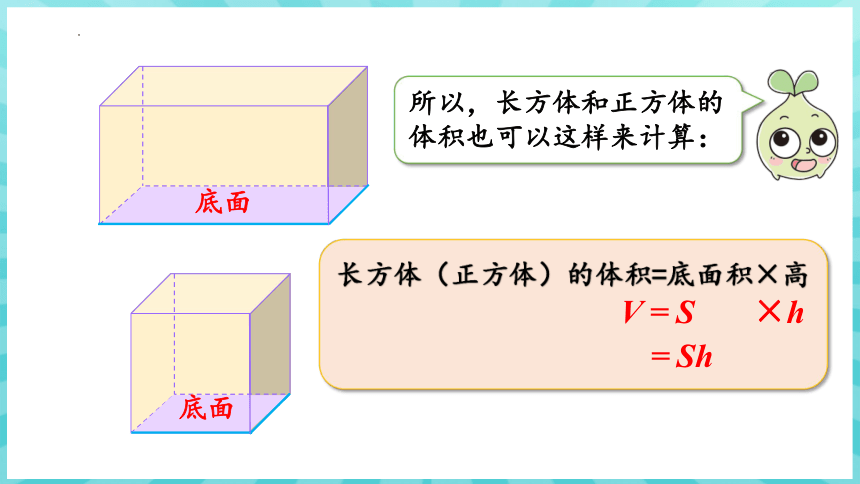
长方体(正方体)的体积=底面积×高
所以,长方体和正方体的体积也可以这样来计算:
V=S ×h
=Sh
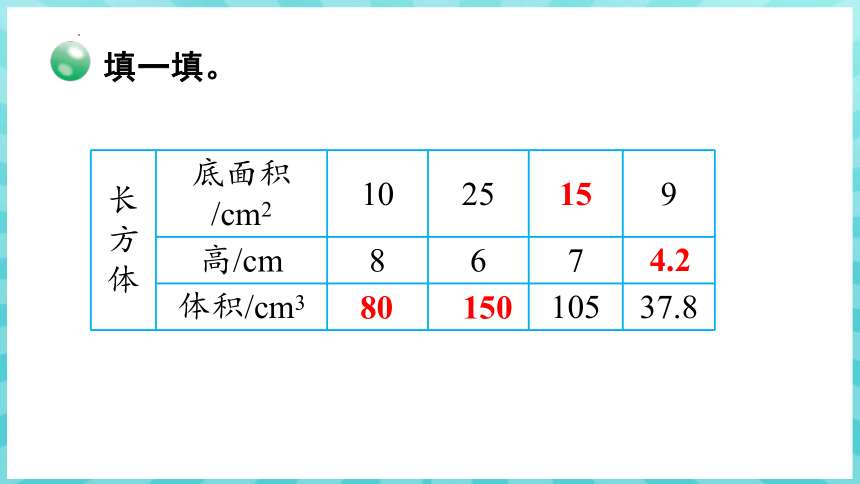
长 方 体 底面积/cm2 10 25 9
高/cm 8 6 7
体积/cm3 105 37.8
80
150
15
4.2
填一填。
64×8=512(立方分米)
答:这块石料的体积是512立方分米。
一块正方体石料,底面面积是64平方分米,棱长是8分米。这块石料的体积是多少立方分米?
1.
V=S×h
一块长方体形状的大理石,体积为30m ,底面是面积为6m 的长方形,这块大理石的高是多少米?
2.
30÷6=5(m)
答:这块大理石的高是5m 。
V=S×h
h=V÷S
96÷(8×8)=1.5(米)
答:这个沙雕底座的高是1.5米。
右图中沙雕作品底座的形状是长方体,它的体积是96立方米,长和宽都是8米。这个沙雕底座的高是多少米?
3.
一个长方体水池,底面长 12 dm,宽 6 dm。如果要向这个池子里注入 2 dm 高的水,需要多少升水?
4.
注的水就是一个长方体,长12dm,宽6dm,宽高2dm 。
12
6
2
12×6×2
=72×2
=144(dm3)
=144(升)
答:需要 144 升水。
一根长1.8米,横截面是25平方厘米的长方体铜条,如果每立方分米重8.9千克,这根铜条共重多少千克?
5.
25平方厘米=0.25平方分米
18×0.25=4.5(dm )
答:这根铜条共重40.05千克。
4.5×8.9=40.05(千克)
1.8米=18分米
正方体铁块的体积: V = a3
= 33
=27(dm3)
长方体铁块的高: 27÷1.5=18(dm)
答:它的高是18dm。
把一块棱长3 dm的正方体铁块,铸造成一个底面积1.5 dm2的长方体铁块,它的高是多少分米?
6.
长方体和正方体铁块的体积相等。
7.下面是一个游泳馆的标示牌:
游泳池规格/m3 50×25×2
建筑总面积/m2 10000
规定游泳池水面低于池口0.6 m,这个游泳池最多盛水多少立
方米?
50×25×(2-0.6)=1750(m3)
答:这个游泳池最多盛水1750 m3。
8.将下面的长方体截成一个体积最大的正方体,这个正方体的体积是多少?结合如图想一想,再算一算。
(单位:cm)
4×4×4=64(cm3)
答:这个正方体的体积是64 cm3。
100÷4=25(dm2)
25×12=300(dm3)
答:原来这根木料的体积是300dm3。
增加了4个面的面积
有一根长12 dm的长方体木料,把它平均锯成3段(如图),表面积增加了100 dm2,原来这根木料的体积是多少?
1.
拓展提升
2.如图,一段长方体木料,长是10 cm,如果锯掉2 cm,它的体积就减少20 cm3。原来这段木料的体积是多少?
20÷2×10=100(cm3)
答:原来这段木料的体积是100 cm3。
体积
1.长方体或正方体底面的面积叫作底面积。
2.长方体(或正方体)的体积=底面积×高
V = Sh
这节课你有哪些收获?
长方体的体积(2)
北师大版五年级数学下册
第四单元 长方体(二)
经历长方体和正方体统一的体积计算公式的推导过程,进一步认识两种几何体的基本特征及它们之间的关系。
理解底面积的基础上掌握长方体和正方体统一的体积计算公式,会应用长方体和正方体统一的体积计算公式解决一些简单的实际问题。
5×3×4
=15×4
=60 (dm3)
2×2×6
=4×6
=24 (dm3)
3×3×3
=9×3
=27 (dm3)
阴影部分的面积是上面各图形底面的面积,称为底面积。
先算一算下列图形的体积,再读一读,想一想。(单位:dm)
底面
底面
长方体底面积=
长×宽
正方体底面积=
棱长×棱长
底面
底面
长方体的体积= 长×宽×高
底面积
高
×
正方体的体积=棱长×棱长×棱长
底面积
=
高
×
=
底面
底面
长方体(正方体)的体积=底面积×高
所以,长方体和正方体的体积也可以这样来计算:
V=S ×h
=Sh
长 方 体 底面积/cm2 10 25 9
高/cm 8 6 7
体积/cm3 105 37.8
80
150
15
4.2
填一填。
64×8=512(立方分米)
答:这块石料的体积是512立方分米。
一块正方体石料,底面面积是64平方分米,棱长是8分米。这块石料的体积是多少立方分米?
1.
V=S×h
一块长方体形状的大理石,体积为30m ,底面是面积为6m 的长方形,这块大理石的高是多少米?
2.
30÷6=5(m)
答:这块大理石的高是5m 。
V=S×h
h=V÷S
96÷(8×8)=1.5(米)
答:这个沙雕底座的高是1.5米。
右图中沙雕作品底座的形状是长方体,它的体积是96立方米,长和宽都是8米。这个沙雕底座的高是多少米?
3.
一个长方体水池,底面长 12 dm,宽 6 dm。如果要向这个池子里注入 2 dm 高的水,需要多少升水?
4.
注的水就是一个长方体,长12dm,宽6dm,宽高2dm 。
12
6
2
12×6×2
=72×2
=144(dm3)
=144(升)
答:需要 144 升水。
一根长1.8米,横截面是25平方厘米的长方体铜条,如果每立方分米重8.9千克,这根铜条共重多少千克?
5.
25平方厘米=0.25平方分米
18×0.25=4.5(dm )
答:这根铜条共重40.05千克。
4.5×8.9=40.05(千克)
1.8米=18分米
正方体铁块的体积: V = a3
= 33
=27(dm3)
长方体铁块的高: 27÷1.5=18(dm)
答:它的高是18dm。
把一块棱长3 dm的正方体铁块,铸造成一个底面积1.5 dm2的长方体铁块,它的高是多少分米?
6.
长方体和正方体铁块的体积相等。
7.下面是一个游泳馆的标示牌:
游泳池规格/m3 50×25×2
建筑总面积/m2 10000
规定游泳池水面低于池口0.6 m,这个游泳池最多盛水多少立
方米?
50×25×(2-0.6)=1750(m3)
答:这个游泳池最多盛水1750 m3。
8.将下面的长方体截成一个体积最大的正方体,这个正方体的体积是多少?结合如图想一想,再算一算。
(单位:cm)
4×4×4=64(cm3)
答:这个正方体的体积是64 cm3。
100÷4=25(dm2)
25×12=300(dm3)
答:原来这根木料的体积是300dm3。
增加了4个面的面积
有一根长12 dm的长方体木料,把它平均锯成3段(如图),表面积增加了100 dm2,原来这根木料的体积是多少?
1.
拓展提升
2.如图,一段长方体木料,长是10 cm,如果锯掉2 cm,它的体积就减少20 cm3。原来这段木料的体积是多少?
20÷2×10=100(cm3)
答:原来这段木料的体积是100 cm3。
体积
1.长方体或正方体底面的面积叫作底面积。
2.长方体(或正方体)的体积=底面积×高
V = Sh
这节课你有哪些收获?
