广东省湛江第一中学2014-2015学年高一下学期期中考试数学试题
文档属性
| 名称 | 广东省湛江第一中学2014-2015学年高一下学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 447.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-18 10:44:53 | ||
图片预览




文档简介
湛江一中2014---2015学年度第二学期期中考试
高一级数学科试卷
考试时间:120分钟 满分:150分
一、选择题:(每小题5分,每题只有一个正确选项,共50分)
1.sin的值是( )
A.- B. C. D.-
2.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是 ( )
A.12,24,15,9 B.9,12,12,7 C.8,15,12,5 D.8,16,10,6
3.已知,且,则的值为( )
A. B. C. D.
4.在区间上随机取一个数,的值介于到1之间的概率是( )
A. B. C. D.
5.已知,则的值为( )
A. B. C. D.
6.从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率为 ( )
A. B. C. D.
7.如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知 ( )
A.甲运动员的最低得分为0分
B.乙运动员得分的中位数是29
C.甲运动员得分的众数为44
D.乙运动员得分的平均值在区间(11,19)内
8.函数的部分图象如图所示,则的值分别是( )
A. B. C. D.
9.某程序框图如右图所示,若输出的,则判断框内为( )
A. B.
C. D.
10.将函数的图象向左平移个单位长度后,所得到的图象关于y轴对称,则的最小值是( )
A. B. C. D
二、填空题:(每小题5分,共20分)
11.化简:= 。
12.某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如下图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生人数是________。
13.若某程序框图如图所示,则该程序运行后输出的的值是________。
14.抛掷两颗骰子出现的点数分别为,则方程有实根的概率为 。
三、解答题:(共80分)
15.(本题12分)某小组共有五位同学,他们的身高(单位:米)及体重指标(单位:千克/米2)如下表所示:
身高 1.69 1.73 1.75 1.79 1.82
体重指标 19.2 25.1 18.5 23.3 20.9
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在
中的概率.
16.(本题12分)一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数 10 15 20 25 30 35 40
件数 4 7 12 15 20 23 27
其中=1,2,3,4,5, 6,7.
(1)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图;
(2)求回归直线方程;(结果四舍五入后保留到小数点后两位)
(3)预测进店人数为80人时,商品销售的件数.(结果保留整数)
(参考公式:)
参考数据:
,
17.(本题14分)已知
(1)求函数的单调递减区间;
(2)若,求的值。
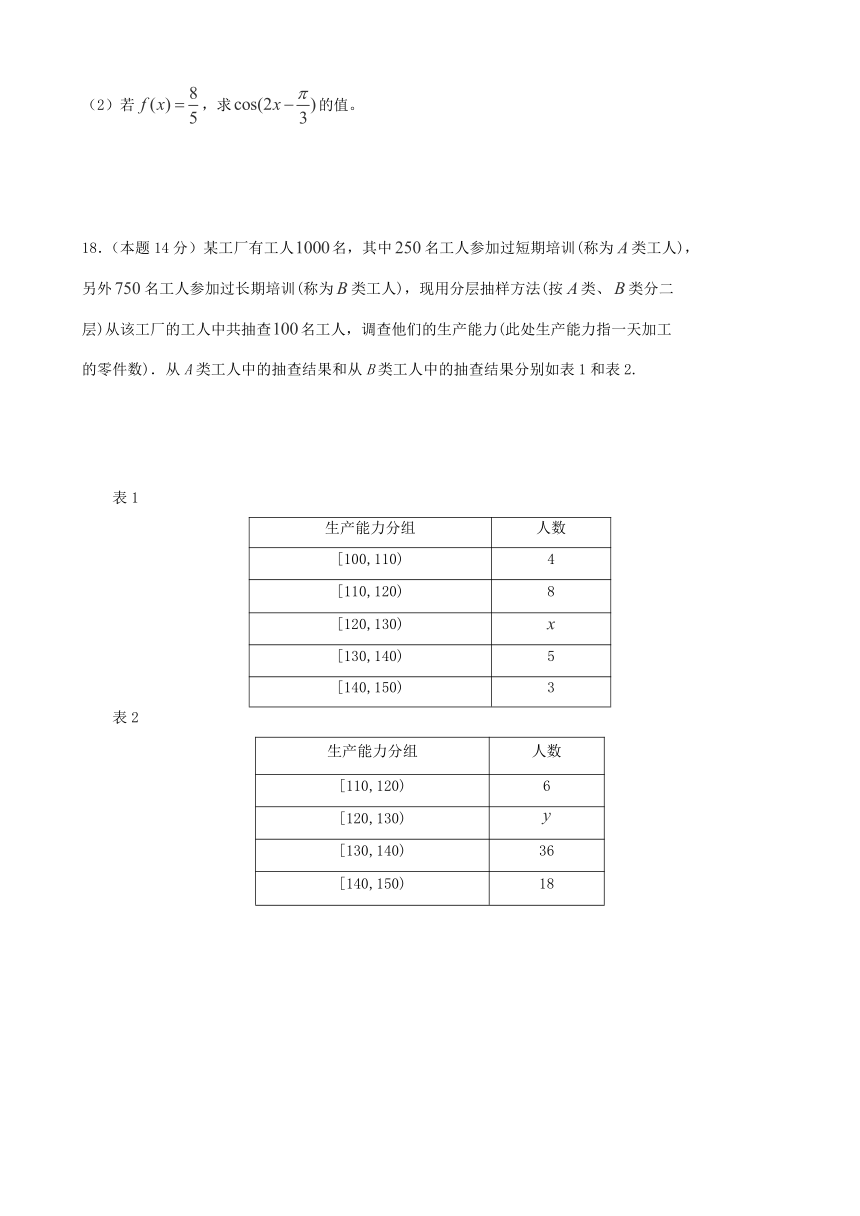
18.(本题14分)某工厂有工人名,其中名工人参加过短期培训(称为类工人),
另外名工人参加过长期培训(称为类工人),现用分层抽样方法(按类、类分二
层)从该工厂的工人中共抽查名工人,调查他们的生产能力(此处生产能力指一天加工
的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1
生产能力分组 人数
[100,110) 4
[110,120) 8
[120,130)
[130,140) 5
[140,150) 3
表2
生产能力分组 人数
[110,120) 6
[120,130)
[130,140) 36
[140,150) 18
(1)先确定,再完成下列频率分布直方图.
(2)估计类工人生产能力的平均数。(同一组中的数据用该组区间的中点值作代表)
19.(本题14分)在如图所示的多面体ABCDE中,BA⊥平面ACD,ED⊥平面ACD,且AC=AD=CD=DE=2,AB=1.
(1)请在线段CE上找到点F的位置,使得恰有 直线BF∥平面ACD,并证明这一事实;
(2)求多面体ABCDE的体积;
(3)求直线EC与平面ABED所成角的正弦值.
20.(本题14分)已知定义在区间上的函数的图像关于直线对称,当时,函数。
(1)求的值;
(2)求的表达式;
(3)若关于的方程有解,那么将方程在取某一确定值时所求得的所有解的和记为,求的所有可能取值及相应的的取值范围。
湛江一中2014---2015学年度第二学期期中考试
高一级数学科试卷答案
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D A C B C A A B
二、填空题:(每小题5分,共20分)
11、-1 12、600 13、5 14、
三、解答题:(共80分)
15.(本题12分)
解:(1)从身高低于的同学中任选人,其一切可能的结果组成的基本事件有: ,共6个.………2分
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的人身高都在以下的事件有,共3个.………4分
因此选到的人身高都在以下的概率为。 …………6分
(2)从该小组同学中任选人,其一切可能的结果组成的基本事件有
,
共10个. ………8分
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人身高都在1.70以上且体重指标都在[18.5,23.9)中的事件有
,共3个. ………10分
因此选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率为
……………12分
16.(本题12分)
解:(1)散点图如图.
……………3分
……………7分
……………9分
∴回归直线方程是……………10分
(3)进店人数为人时,商品销售的件数.…………12分
17.(本题14分)
解:(1)
…………3分
令 ………6分
故的单调递减区间是 …………7分
(2)由(1)得.
…………9分
…………12分
…………14分
18.(本题14分)
解:(1)由题意知,类工人中应抽查25名,B类工人中应抽查75名. …………1分
故4+8++5+3=25,得=5,
,得. ……………3分
频率分布直方图如图:……………11分
(2)A=105+115+125+135+145=123,………11分
类工人生产能力平均数的估计值为123。
………14分
19.(本题14分)
解:如图,(1)由已知BA⊥平面ACD,ED⊥平面ACD,∴AB//ED,
设F为线段CE的中点,……………1分
H是线段CD的中点,连接FH,则,
∴, ……………2分
∴四边形ABFH是平行四边形,∴,
由平面ACD内,平面ACD,
平面ACD;…………4分
(2)取AD中点G,连接CG.. ……………5分
AB平面ACD, ∴CGAB
又CGAD ∴CG平面ABED, 即CG为四棱锥的高, ………6分CG= ……………7分
∴=2=. ……………8分
(3)连接EG,由(2)有CG平面ABED,
∴即为直线CE与平面ABED所成的角, ………10分
设为,则在中,
有. ……………13分
故直线EC与平面ABED所成角的正弦值为。 ……………14分
20.(本题14分)
(1),
。 ………2分
(2)设 ………3分
………5分
………6分
(3)作函数的图像,………7分
显然,若有解,则。 ………9分
①若,有两解,; ………10分
②若,有三解,; ………11分
③若,有四解, ………12分
④若,有两解,。 ………13分
综上所述,当时,有两解,;
当时,有三解,;
当时,有四解,。 ………14分
F
G
C
D
A
B
0 8
0 1 2 4 7
3 2 2 1 9 9
5 4 2 1 3 3 6
4 4 4
1 5 2
乙
甲
E
H
O
x
y
高一级数学科试卷
考试时间:120分钟 满分:150分
一、选择题:(每小题5分,每题只有一个正确选项,共50分)
1.sin的值是( )
A.- B. C. D.-
2.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是 ( )
A.12,24,15,9 B.9,12,12,7 C.8,15,12,5 D.8,16,10,6
3.已知,且,则的值为( )
A. B. C. D.
4.在区间上随机取一个数,的值介于到1之间的概率是( )
A. B. C. D.
5.已知,则的值为( )
A. B. C. D.
6.从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率为 ( )
A. B. C. D.
7.如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知 ( )
A.甲运动员的最低得分为0分
B.乙运动员得分的中位数是29
C.甲运动员得分的众数为44
D.乙运动员得分的平均值在区间(11,19)内
8.函数的部分图象如图所示,则的值分别是( )
A. B. C. D.
9.某程序框图如右图所示,若输出的,则判断框内为( )
A. B.
C. D.
10.将函数的图象向左平移个单位长度后,所得到的图象关于y轴对称,则的最小值是( )
A. B. C. D
二、填空题:(每小题5分,共20分)
11.化简:= 。
12.某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如下图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生人数是________。
13.若某程序框图如图所示,则该程序运行后输出的的值是________。
14.抛掷两颗骰子出现的点数分别为,则方程有实根的概率为 。
三、解答题:(共80分)
15.(本题12分)某小组共有五位同学,他们的身高(单位:米)及体重指标(单位:千克/米2)如下表所示:
身高 1.69 1.73 1.75 1.79 1.82
体重指标 19.2 25.1 18.5 23.3 20.9
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在
中的概率.
16.(本题12分)一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数 10 15 20 25 30 35 40
件数 4 7 12 15 20 23 27
其中=1,2,3,4,5, 6,7.
(1)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图;
(2)求回归直线方程;(结果四舍五入后保留到小数点后两位)
(3)预测进店人数为80人时,商品销售的件数.(结果保留整数)
(参考公式:)
参考数据:
,
17.(本题14分)已知
(1)求函数的单调递减区间;
(2)若,求的值。
18.(本题14分)某工厂有工人名,其中名工人参加过短期培训(称为类工人),
另外名工人参加过长期培训(称为类工人),现用分层抽样方法(按类、类分二
层)从该工厂的工人中共抽查名工人,调查他们的生产能力(此处生产能力指一天加工
的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1
生产能力分组 人数
[100,110) 4
[110,120) 8
[120,130)
[130,140) 5
[140,150) 3
表2
生产能力分组 人数
[110,120) 6
[120,130)
[130,140) 36
[140,150) 18
(1)先确定,再完成下列频率分布直方图.
(2)估计类工人生产能力的平均数。(同一组中的数据用该组区间的中点值作代表)
19.(本题14分)在如图所示的多面体ABCDE中,BA⊥平面ACD,ED⊥平面ACD,且AC=AD=CD=DE=2,AB=1.
(1)请在线段CE上找到点F的位置,使得恰有 直线BF∥平面ACD,并证明这一事实;
(2)求多面体ABCDE的体积;
(3)求直线EC与平面ABED所成角的正弦值.
20.(本题14分)已知定义在区间上的函数的图像关于直线对称,当时,函数。
(1)求的值;
(2)求的表达式;
(3)若关于的方程有解,那么将方程在取某一确定值时所求得的所有解的和记为,求的所有可能取值及相应的的取值范围。
湛江一中2014---2015学年度第二学期期中考试
高一级数学科试卷答案
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D A C B C A A B
二、填空题:(每小题5分,共20分)
11、-1 12、600 13、5 14、
三、解答题:(共80分)
15.(本题12分)
解:(1)从身高低于的同学中任选人,其一切可能的结果组成的基本事件有: ,共6个.………2分
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的人身高都在以下的事件有,共3个.………4分
因此选到的人身高都在以下的概率为。 …………6分
(2)从该小组同学中任选人,其一切可能的结果组成的基本事件有
,
共10个. ………8分
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人身高都在1.70以上且体重指标都在[18.5,23.9)中的事件有
,共3个. ………10分
因此选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率为
……………12分
16.(本题12分)
解:(1)散点图如图.
……………3分
……………7分
……………9分
∴回归直线方程是……………10分
(3)进店人数为人时,商品销售的件数.…………12分
17.(本题14分)
解:(1)
…………3分
令 ………6分
故的单调递减区间是 …………7分
(2)由(1)得.
…………9分
…………12分
…………14分
18.(本题14分)
解:(1)由题意知,类工人中应抽查25名,B类工人中应抽查75名. …………1分
故4+8++5+3=25,得=5,
,得. ……………3分
频率分布直方图如图:……………11分
(2)A=105+115+125+135+145=123,………11分
类工人生产能力平均数的估计值为123。
………14分
19.(本题14分)
解:如图,(1)由已知BA⊥平面ACD,ED⊥平面ACD,∴AB//ED,
设F为线段CE的中点,……………1分
H是线段CD的中点,连接FH,则,
∴, ……………2分
∴四边形ABFH是平行四边形,∴,
由平面ACD内,平面ACD,
平面ACD;…………4分
(2)取AD中点G,连接CG.. ……………5分
AB平面ACD, ∴CGAB
又CGAD ∴CG平面ABED, 即CG为四棱锥的高, ………6分CG= ……………7分
∴=2=. ……………8分
(3)连接EG,由(2)有CG平面ABED,
∴即为直线CE与平面ABED所成的角, ………10分
设为,则在中,
有. ……………13分
故直线EC与平面ABED所成角的正弦值为。 ……………14分
20.(本题14分)
(1),
。 ………2分
(2)设 ………3分
………5分
………6分
(3)作函数的图像,………7分
显然,若有解,则。 ………9分
①若,有两解,; ………10分
②若,有三解,; ………11分
③若,有四解, ………12分
④若,有两解,。 ………13分
综上所述,当时,有两解,;
当时,有三解,;
当时,有四解,。 ………14分
F
G
C
D
A
B
0 8
0 1 2 4 7
3 2 2 1 9 9
5 4 2 1 3 3 6
4 4 4
1 5 2
乙
甲
E
H
O
x
y
同课章节目录
