第二单元《梯形的面积》课件(共17张PPT)五年级上册数学苏教版
文档属性
| 名称 | 第二单元《梯形的面积》课件(共17张PPT)五年级上册数学苏教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 949.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 06:14:54 | ||
图片预览





文档简介
(共17张PPT)
多边形的面积
第二单元
三、求梯形的面积 。
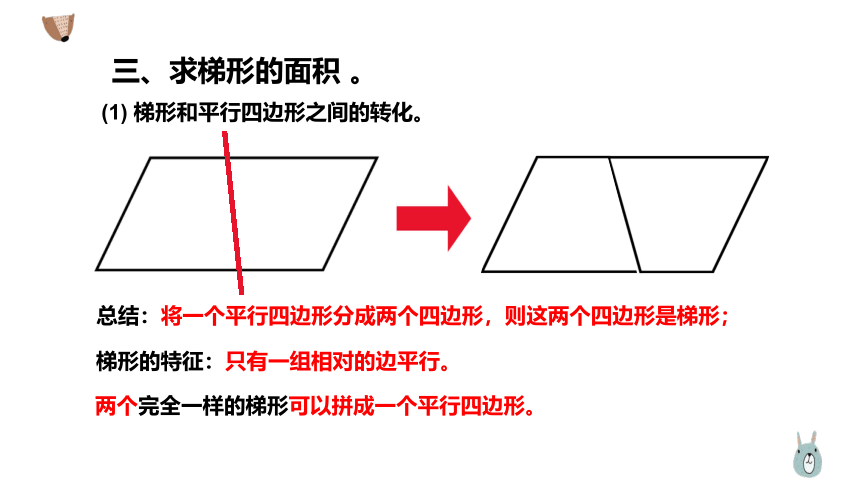
(1) 梯形和平行四边形之间的转化。
总结:将一个平行四边形分成两个四边形,则这两个四边形是梯形;
梯形的特征:只有一组相对的边平行。
两个完全一样的梯形可以拼成一个平行四边形。
三、求梯形的面积 。
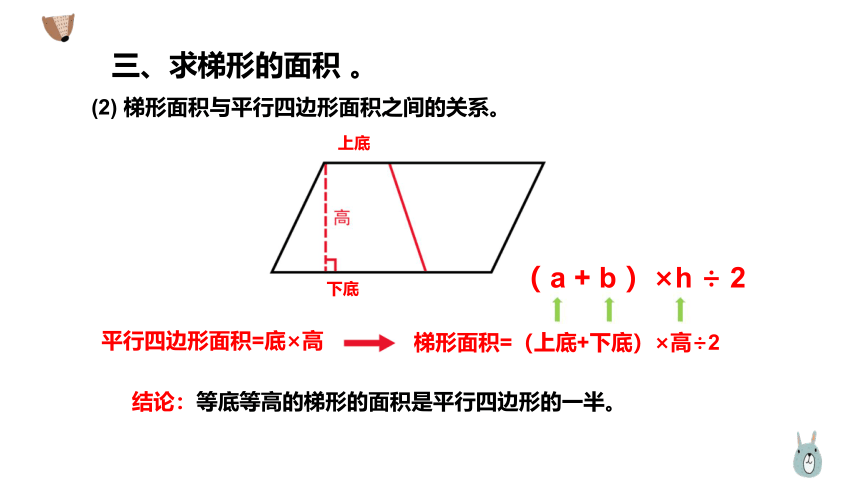
平行四边形面积=底×高
结论:等底等高的梯形的面积是平行四边形的一半。
(2) 梯形面积与平行四边形面积之间的关系。
梯形面积=(上底+下底)×高÷2
上底
下底
( a + b )×h ÷ 2
例题讲解:
例1: 两个完全相同的梯形可以拼成一个( )。这个平行四边形的底等于( ),平行四边形的高等于( )。每个梯形的面积等于拼成的平行四边形的面积的( ),因为平行四边形的面积等于( ),所以梯形的面积等于:
例2: 一个长方形被分割成两个完全一样的梯形。如果长方形的长是10cm,
宽是5cm,那么其中一个梯形的面积是( )。
10×5=50(cm )
平行四边形
梯形的上底+下底
梯形的高
一半
底×高
(上底+下底 )×高÷2
50÷2=25(cm )
25cm
例题演练:
例1: 一个梯形的面积是42平方米,它的上、下底之和与一个平行四
边形的底边相等,高与平行四边形的高相等,这个平行四边形
的面积是( )平方米。
例2:一个梯形的装饰板,上底6分米,下底10分米,高1米,两面都要
涂油漆,涂油漆的面积是( )平方分米
例: 已知梯形的上底是18分米,是下底的2倍,高是6分米,梯形的面积是( )平方分米。
84
160
动脑思考
三、求梯形的面积 。
(3) 梯形的面积的逆公式。
已知:梯形面积=(上底+下底)×高÷2,上底+下底的和为10+8=18cm,
梯形的面积为45cm ,所以梯形的高为:45×2÷18=5 (cm)
例1:一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形
的高是多少厘米
例2:一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形
的高是多少厘米
例题变形:
例3:一个梯形的面积是24平方分米,下底是7分米,高是40厘米,上底是( )分米。
解析、因为梯形面积=(上底+下底)×高÷2,梯形的面积为24平方分米,梯形的高为40厘米即4分米,所以梯形:上底+下底的和为梯形面积×2÷高 = 24×2÷4=12dm,梯形下底是7dm,则上底是5dm。
例: 一个梯形上底是16分米,高是20分米,两个这样的梯形面积
是12平方米,这个梯形的下底长多少分米
5
动脑思考
三、求梯形的面积 。
(4) 梯形底和高的变化与面积变化的关系。
梯形面积 = (上底 + 下底 )×高 ÷ 2
例1:一个梯形原来的面积是180平方厘米,如果它的上底、下底均不变,高扩大到原来的2倍,那么现在的面积是( )平方厘米;如果它的上底和下底都扩大3倍,高不变,那么现在的面积是( )平方厘米。
梯形面积 =(上底+下底 )× 高 ÷ 2
360
540
三、求梯形的面积 。
(5) 梯形面积公式的综合应用。
例1:一个直角梯形,如果上底增加2厘米,就成为一个边长为4厘米的正方形,这个梯形的面积是( )平方厘米。
解析、如果上底增加2厘米后就变成边长为4厘米的正方形,所以直角梯形的高为4厘米,下底也为4厘米,上底为4-2=2厘米,梯形面积=(2+4)×4÷2=12平方厘米。
12
例题演练:
例1: 一个梯形上底和下底的平均数是8厘米,高是4厘米,它的面积
是( )平方厘米。
例2:一个梯形,上底是5厘米,下底是7厘米,如果只把它的下底增加
3厘米,那么面积就增加9平方厘米。求原梯形的面积。
32
9cm
三、求梯形的面积 。
(5) 篱笆问题。
例1:张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,篱笆长50米,
鸡舍的面积是多少平方米
梯形面积 =(上底+下底)×高÷2
动脑思考
: 张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,
篱笆长50米,鸡舍的面积是多少平方米
三、求梯形的面积 。
(6) 运用分析法解决梯形中求面积最大的问题。
例1:在一个上底是11分米,下底是18分米,高是22分米的梯形中,剪下一个
最大的三角形,剩下的面积是多少
解析、在梯形中剪下一个最大的三角形,则以
梯形的下底为三角形的底,梯形的高为三角形的
高,此时三角形的底最大,高最大,所以三角形的面积最大,
11×22÷2=121(dm )
例题演练:
例1: 在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少
例2:已知一个梯形上底是8厘米,下底是15cm,
在这个梯形中剪去一个最大的三角形,剩下的
面积是20平方厘米。原来梯形的面积是多少
(7-5)×4÷2=4(cm )
7-5
三、求梯形的面积 。
(7) 添加辅助线解题。
例1:如图,平行四边形的面积是40平方分米,M是平行四边形底边上的中点,
则图中三角形的面积是( )平方分米,梯形的面积是( )平方分米。
10
30
例2:如图,平行四边形的面积是30cm ,M是平行四边形底边
上的中点,则图中三角形的面积是( )cm ,梯形的面
积是( )cm 。
225
三、求梯形的面积 。
(8) 堆木头问题。
例1: 工地上有一堆木头,横截面是一个梯形,已知最上面一层有2根,
最下面一层有12根,共堆了11层,这堆木头共有多少根?
解析、这堆木头的截面是梯形,最上面一层有2根,看成梯形上底为2;最下面一层有12根,看成下底为12;有11层看成梯形的高为11。则梯形的面积=(2+12)×11÷2 = 77,所以有77根木头。
例题演练:
例1: 一堆钢管,最上面一层有10根,最下面一层有20根,而且下一
层总比上一层多1根。这堆钢管一共有多少根?
解析、这堆钢管的横截面是梯形,上底为10根,下底是20根,要想
求梯形的面积就要知道梯形的高,也就是这堆钢管一共有多少层;钢管的层数=最下层数量-最上层数量+1,也就是20-10+1=11层,所以这堆钢管有:(20+10)×11÷2=165(根)
总结:当下一层比上一层多一根时,层数=最下层数量-最上层数量+1
三、求梯形的面积 。
(9) 转化法求阴影部分的面积。
例1: 右下图是两个完全相同的直角三角形部分重叠在一起,求阴影部分
的面积。(单位:分米)
(8+5)×4÷2=26(平方分米)
4
例2: 如右图两个相同的直角梯形重叠在一起,
求阴影部分的面积。(单位:厘米)
多边形的面积
第二单元
三、求梯形的面积 。
(1) 梯形和平行四边形之间的转化。
总结:将一个平行四边形分成两个四边形,则这两个四边形是梯形;
梯形的特征:只有一组相对的边平行。
两个完全一样的梯形可以拼成一个平行四边形。
三、求梯形的面积 。
平行四边形面积=底×高
结论:等底等高的梯形的面积是平行四边形的一半。
(2) 梯形面积与平行四边形面积之间的关系。
梯形面积=(上底+下底)×高÷2
上底
下底
( a + b )×h ÷ 2
例题讲解:
例1: 两个完全相同的梯形可以拼成一个( )。这个平行四边形的底等于( ),平行四边形的高等于( )。每个梯形的面积等于拼成的平行四边形的面积的( ),因为平行四边形的面积等于( ),所以梯形的面积等于:
例2: 一个长方形被分割成两个完全一样的梯形。如果长方形的长是10cm,
宽是5cm,那么其中一个梯形的面积是( )。
10×5=50(cm )
平行四边形
梯形的上底+下底
梯形的高
一半
底×高
(上底+下底 )×高÷2
50÷2=25(cm )
25cm
例题演练:
例1: 一个梯形的面积是42平方米,它的上、下底之和与一个平行四
边形的底边相等,高与平行四边形的高相等,这个平行四边形
的面积是( )平方米。
例2:一个梯形的装饰板,上底6分米,下底10分米,高1米,两面都要
涂油漆,涂油漆的面积是( )平方分米
例: 已知梯形的上底是18分米,是下底的2倍,高是6分米,梯形的面积是( )平方分米。
84
160
动脑思考
三、求梯形的面积 。
(3) 梯形的面积的逆公式。
已知:梯形面积=(上底+下底)×高÷2,上底+下底的和为10+8=18cm,
梯形的面积为45cm ,所以梯形的高为:45×2÷18=5 (cm)
例1:一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形
的高是多少厘米
例2:一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形
的高是多少厘米
例题变形:
例3:一个梯形的面积是24平方分米,下底是7分米,高是40厘米,上底是( )分米。
解析、因为梯形面积=(上底+下底)×高÷2,梯形的面积为24平方分米,梯形的高为40厘米即4分米,所以梯形:上底+下底的和为梯形面积×2÷高 = 24×2÷4=12dm,梯形下底是7dm,则上底是5dm。
例: 一个梯形上底是16分米,高是20分米,两个这样的梯形面积
是12平方米,这个梯形的下底长多少分米
5
动脑思考
三、求梯形的面积 。
(4) 梯形底和高的变化与面积变化的关系。
梯形面积 = (上底 + 下底 )×高 ÷ 2
例1:一个梯形原来的面积是180平方厘米,如果它的上底、下底均不变,高扩大到原来的2倍,那么现在的面积是( )平方厘米;如果它的上底和下底都扩大3倍,高不变,那么现在的面积是( )平方厘米。
梯形面积 =(上底+下底 )× 高 ÷ 2
360
540
三、求梯形的面积 。
(5) 梯形面积公式的综合应用。
例1:一个直角梯形,如果上底增加2厘米,就成为一个边长为4厘米的正方形,这个梯形的面积是( )平方厘米。
解析、如果上底增加2厘米后就变成边长为4厘米的正方形,所以直角梯形的高为4厘米,下底也为4厘米,上底为4-2=2厘米,梯形面积=(2+4)×4÷2=12平方厘米。
12
例题演练:
例1: 一个梯形上底和下底的平均数是8厘米,高是4厘米,它的面积
是( )平方厘米。
例2:一个梯形,上底是5厘米,下底是7厘米,如果只把它的下底增加
3厘米,那么面积就增加9平方厘米。求原梯形的面积。
32
9cm
三、求梯形的面积 。
(5) 篱笆问题。
例1:张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,篱笆长50米,
鸡舍的面积是多少平方米
梯形面积 =(上底+下底)×高÷2
动脑思考
: 张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,
篱笆长50米,鸡舍的面积是多少平方米
三、求梯形的面积 。
(6) 运用分析法解决梯形中求面积最大的问题。
例1:在一个上底是11分米,下底是18分米,高是22分米的梯形中,剪下一个
最大的三角形,剩下的面积是多少
解析、在梯形中剪下一个最大的三角形,则以
梯形的下底为三角形的底,梯形的高为三角形的
高,此时三角形的底最大,高最大,所以三角形的面积最大,
11×22÷2=121(dm )
例题演练:
例1: 在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少
例2:已知一个梯形上底是8厘米,下底是15cm,
在这个梯形中剪去一个最大的三角形,剩下的
面积是20平方厘米。原来梯形的面积是多少
(7-5)×4÷2=4(cm )
7-5
三、求梯形的面积 。
(7) 添加辅助线解题。
例1:如图,平行四边形的面积是40平方分米,M是平行四边形底边上的中点,
则图中三角形的面积是( )平方分米,梯形的面积是( )平方分米。
10
30
例2:如图,平行四边形的面积是30cm ,M是平行四边形底边
上的中点,则图中三角形的面积是( )cm ,梯形的面
积是( )cm 。
225
三、求梯形的面积 。
(8) 堆木头问题。
例1: 工地上有一堆木头,横截面是一个梯形,已知最上面一层有2根,
最下面一层有12根,共堆了11层,这堆木头共有多少根?
解析、这堆木头的截面是梯形,最上面一层有2根,看成梯形上底为2;最下面一层有12根,看成下底为12;有11层看成梯形的高为11。则梯形的面积=(2+12)×11÷2 = 77,所以有77根木头。
例题演练:
例1: 一堆钢管,最上面一层有10根,最下面一层有20根,而且下一
层总比上一层多1根。这堆钢管一共有多少根?
解析、这堆钢管的横截面是梯形,上底为10根,下底是20根,要想
求梯形的面积就要知道梯形的高,也就是这堆钢管一共有多少层;钢管的层数=最下层数量-最上层数量+1,也就是20-10+1=11层,所以这堆钢管有:(20+10)×11÷2=165(根)
总结:当下一层比上一层多一根时,层数=最下层数量-最上层数量+1
三、求梯形的面积 。
(9) 转化法求阴影部分的面积。
例1: 右下图是两个完全相同的直角三角形部分重叠在一起,求阴影部分
的面积。(单位:分米)
(8+5)×4÷2=26(平方分米)
4
例2: 如右图两个相同的直角梯形重叠在一起,
求阴影部分的面积。(单位:厘米)
