《多边形的面积》课件(共19张PPT)五年级上册数学苏教版
文档属性
| 名称 | 《多边形的面积》课件(共19张PPT)五年级上册数学苏教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 990.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 06:16:31 | ||
图片预览


文档简介
(共19张PPT)
多边形的面积
第二单元
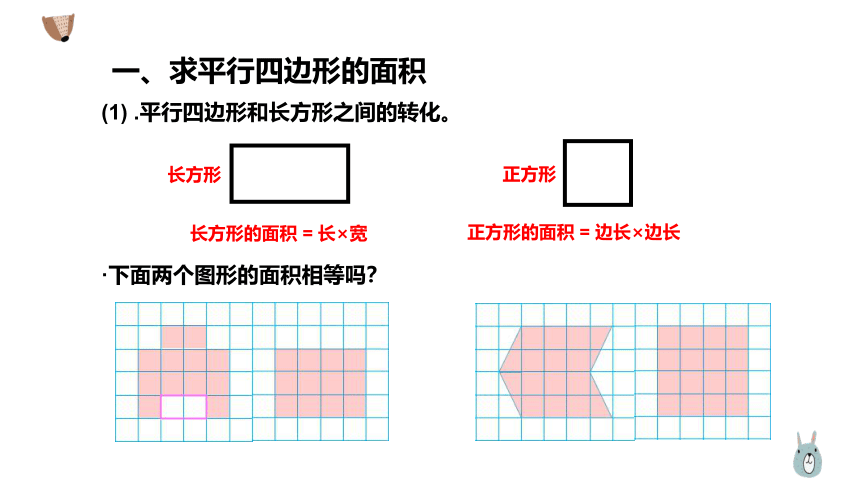
一、求平行四边形的面积
(1) .平行四边形和长方形之间的转化。
·下面两个图形的面积相等吗?
长方形
正方形
长方形的面积 = 长×宽
正方形的面积 = 边长×边长
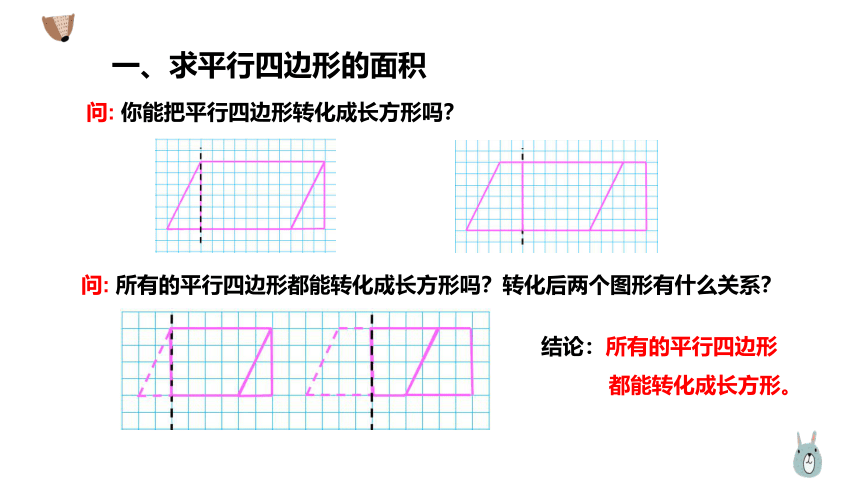
一、求平行四边形的面积
问: 你能把平行四边形转化成长方形吗?
问: 所有的平行四边形都能转化成长方形吗?转化后两个图形有什么关系?
结论:所有的平行四边形
都能转化成长方形。
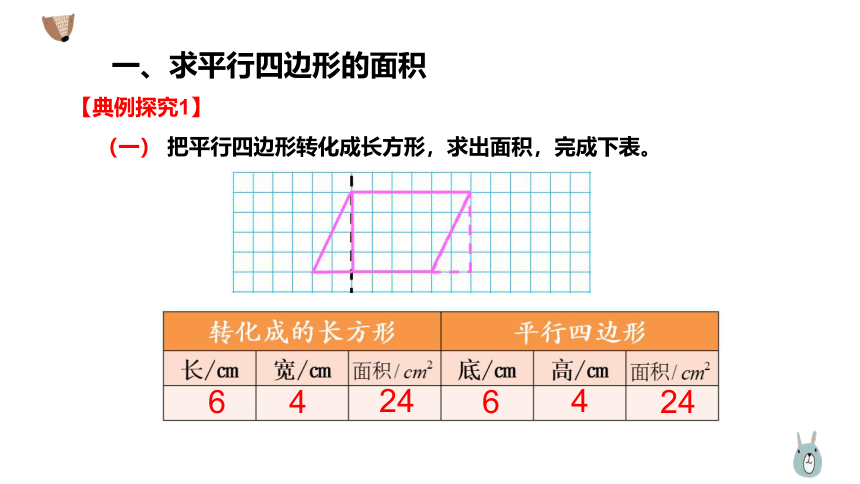
一、求平行四边形的面积
【典例探究1】
(一) 把平行四边形转化成长方形,求出面积,完成下表。
6
4
24
6
4
24
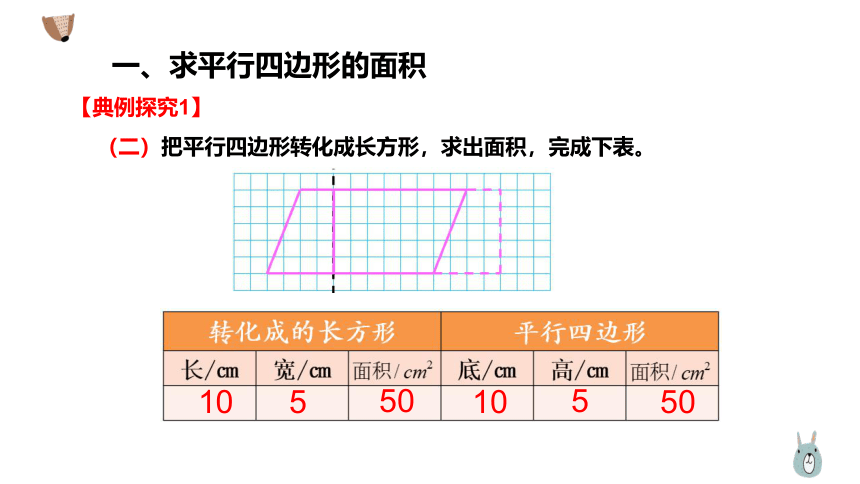
一、求平行四边形的面积
【典例探究1】
(二)把平行四边形转化成长方形,求出面积,完成下表。
10
5
50
10
5
50
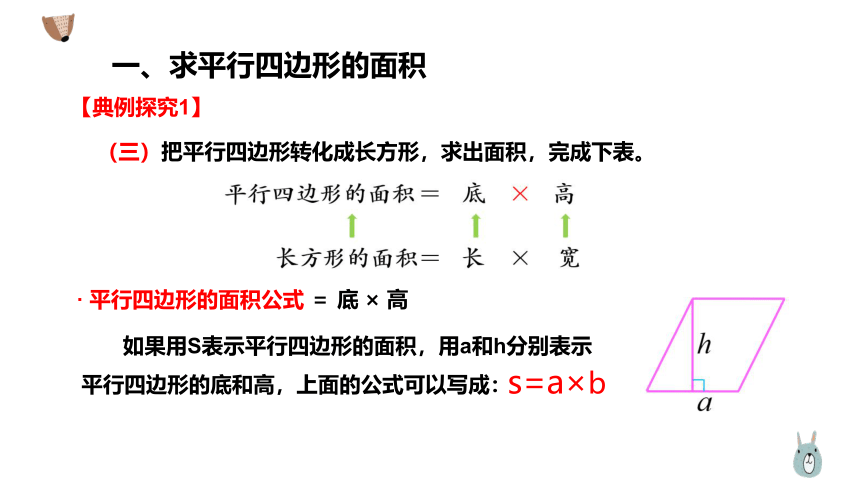
一、求平行四边形的面积
【典例探究1】
(三)把平行四边形转化成长方形,求出面积,完成下表。
· 平行四边形的面积公式
= 底 × 高
如果用S表示平行四边形的面积,用a和h分别表示
平行四边形的底和高,上面的公式可以写成:
s=a×b
例题讲解:
例1: 一个平行四边形,底50厘米,高70厘米,面积是多少平方厘米?
例2: 平行四边形的底是15米,高是8米,它的面积是( )平方米。
s=a×b
s=50×70 = 3500(平方厘米)
答:平行四边形的面积是3500平方厘米。
解析: 根据平行四边形的面积公式=底×高, 得:15×8=120平方米。
120
变式: 一个平行四边形的面积是24平方米,底是8米。它的高是多少米
解析: 根据平行四边形的面积公式=底×高,得:高 = 面积 ÷ 底
高 = 24÷8=3(米)
例题演练:
例1: 填表。
例2:李伯伯家有一个平行四边形的香蕉园,底是160米,底是高的2倍,那么这个香蕉园的面积是多少平方米?
60cm
16dm
12m
解析: 根据题意,底是高的2倍得,底是160米,高为320米,
所以香蕉园的面积为:320×160 = 51200(平方米)
例题演练:
例2:找准对应量解决问题。
1. 一个平行四边形的高是10厘米,相邻的两条边的长度分别是8厘米和12厘米。这个平行四边形的面积是多少平方厘米?
总结:已知平行四边形一组相邻的边长和一条高,高长在两边长度之间时,
要以平行四边形的短边为底。
S=8×10=80(cm )
例题变形:
例3: 一个平行四边形相邻两条边的长分别是16厘米和28厘米,它的一条高是19厘米。这个平行四边形的面积是多少平方厘米
解析、因为相邻的一组边为16和28厘米,一条高19厘米,在16厘米和28厘米之间,所以我们以短边为底,则平行四边形的面积为:
16×19= 304(cm )
例4: 如图,平行四边形的周长是46厘米,则其面积是多少平方厘米
46÷2-10=13(cm)
13×7=91 (cm )
例题变形:
例5: 如右图所示,李大爷要围一块这样的平行四边形菜地,至
少需要铁丝网多少米
20×12=240(m )
解析、求需要钢丝多少米就是求平行四边形菜地
的周长,已知平行四边形的一条边为20,只要求出
另一条边就可以求出周长。
240÷16=15(m)
15m
(20+15)×2=70(m)
答:至少需要铁丝网70米。
一、求平行四边形的面积
【典例探究2】
(四)平行四边形和长方形综合考察。
A
例: 用细木条钉成一个长方形框架,拉成一个平行四边形后,
周长( ),面积( )。
C
例题讲解:
例1: 有一个活动的平行四边形框架,周长是42厘米,底是12厘米,拉伸使它变形到面积最大,最大面积是( )平方厘米。
解析、因为平行四边形的周长是42厘米,所以相邻的两条边长
之和为21厘米,底是12厘米,所以另一条边长21-12=9厘米,当平行四边形变成长方形的时候面积最大,即:12×9=108cm 。
42÷2=21cm
21-12=9 cm
12×9=108 cm
108
例题变形:
例1: 冬冬用木条钉成一个底是16cm、高是8cm的平行四边形,把它拉成一个长方形,面积增加了32cm 。这个长方形的周长是多少
解析、将一个平行四边形拉成一个长方形底16cm不变,面积增加32cm ,则高增加32÷16=2厘米,平行四边形的高是8cm,增加2厘米后是10cm,则长方形的宽为10cm,周长为(16+10)×2=52(cm)
32÷16=2(cm) 8+2=10(cm) (16+10)×2=52(cm)
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)求阴影部分面积。
例1:求下图中阴影部分的面积。(单位:cm)
一、求平行四边形的面积
【典例探究2】
(五)求阴影部分面积。
例1:下图中正方形的周长是32厘米,求平行四边形的面积。
多边形的面积
第二单元
一、求平行四边形的面积
(1) .平行四边形和长方形之间的转化。
·下面两个图形的面积相等吗?
长方形
正方形
长方形的面积 = 长×宽
正方形的面积 = 边长×边长
一、求平行四边形的面积
问: 你能把平行四边形转化成长方形吗?
问: 所有的平行四边形都能转化成长方形吗?转化后两个图形有什么关系?
结论:所有的平行四边形
都能转化成长方形。
一、求平行四边形的面积
【典例探究1】
(一) 把平行四边形转化成长方形,求出面积,完成下表。
6
4
24
6
4
24
一、求平行四边形的面积
【典例探究1】
(二)把平行四边形转化成长方形,求出面积,完成下表。
10
5
50
10
5
50
一、求平行四边形的面积
【典例探究1】
(三)把平行四边形转化成长方形,求出面积,完成下表。
· 平行四边形的面积公式
= 底 × 高
如果用S表示平行四边形的面积,用a和h分别表示
平行四边形的底和高,上面的公式可以写成:
s=a×b
例题讲解:
例1: 一个平行四边形,底50厘米,高70厘米,面积是多少平方厘米?
例2: 平行四边形的底是15米,高是8米,它的面积是( )平方米。
s=a×b
s=50×70 = 3500(平方厘米)
答:平行四边形的面积是3500平方厘米。
解析: 根据平行四边形的面积公式=底×高, 得:15×8=120平方米。
120
变式: 一个平行四边形的面积是24平方米,底是8米。它的高是多少米
解析: 根据平行四边形的面积公式=底×高,得:高 = 面积 ÷ 底
高 = 24÷8=3(米)
例题演练:
例1: 填表。
例2:李伯伯家有一个平行四边形的香蕉园,底是160米,底是高的2倍,那么这个香蕉园的面积是多少平方米?
60cm
16dm
12m
解析: 根据题意,底是高的2倍得,底是160米,高为320米,
所以香蕉园的面积为:320×160 = 51200(平方米)
例题演练:
例2:找准对应量解决问题。
1. 一个平行四边形的高是10厘米,相邻的两条边的长度分别是8厘米和12厘米。这个平行四边形的面积是多少平方厘米?
总结:已知平行四边形一组相邻的边长和一条高,高长在两边长度之间时,
要以平行四边形的短边为底。
S=8×10=80(cm )
例题变形:
例3: 一个平行四边形相邻两条边的长分别是16厘米和28厘米,它的一条高是19厘米。这个平行四边形的面积是多少平方厘米
解析、因为相邻的一组边为16和28厘米,一条高19厘米,在16厘米和28厘米之间,所以我们以短边为底,则平行四边形的面积为:
16×19= 304(cm )
例4: 如图,平行四边形的周长是46厘米,则其面积是多少平方厘米
46÷2-10=13(cm)
13×7=91 (cm )
例题变形:
例5: 如右图所示,李大爷要围一块这样的平行四边形菜地,至
少需要铁丝网多少米
20×12=240(m )
解析、求需要钢丝多少米就是求平行四边形菜地
的周长,已知平行四边形的一条边为20,只要求出
另一条边就可以求出周长。
240÷16=15(m)
15m
(20+15)×2=70(m)
答:至少需要铁丝网70米。
一、求平行四边形的面积
【典例探究2】
(四)平行四边形和长方形综合考察。
A
例: 用细木条钉成一个长方形框架,拉成一个平行四边形后,
周长( ),面积( )。
C
例题讲解:
例1: 有一个活动的平行四边形框架,周长是42厘米,底是12厘米,拉伸使它变形到面积最大,最大面积是( )平方厘米。
解析、因为平行四边形的周长是42厘米,所以相邻的两条边长
之和为21厘米,底是12厘米,所以另一条边长21-12=9厘米,当平行四边形变成长方形的时候面积最大,即:12×9=108cm 。
42÷2=21cm
21-12=9 cm
12×9=108 cm
108
例题变形:
例1: 冬冬用木条钉成一个底是16cm、高是8cm的平行四边形,把它拉成一个长方形,面积增加了32cm 。这个长方形的周长是多少
解析、将一个平行四边形拉成一个长方形底16cm不变,面积增加32cm ,则高增加32÷16=2厘米,平行四边形的高是8cm,增加2厘米后是10cm,则长方形的宽为10cm,周长为(16+10)×2=52(cm)
32÷16=2(cm) 8+2=10(cm) (16+10)×2=52(cm)
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)平行四边形底和高的变化与面积变化的变化.
例1:平行四边形的高扩大到原来的3倍,底不变,面积( )
解析、假设平行四边形的底为a,高为h,高扩大3倍为3h,则原来
平行四边形的面积是ah,扩大后的面积为3ah。所以面积也扩大3倍。
扩大3倍
动脑思考
平行四边形的底扩大3倍,高扩大2倍,则平行四边形的面积( )。
一、求平行四边形的面积
【典例探究2】
(五)求阴影部分面积。
例1:求下图中阴影部分的面积。(单位:cm)
一、求平行四边形的面积
【典例探究2】
(五)求阴影部分面积。
例1:下图中正方形的周长是32厘米,求平行四边形的面积。
