1.2.3 绝对值2023-2024学年 课件 (共15张PPT)湘教版七年级上册数学
文档属性
| 名称 | 1.2.3 绝对值2023-2024学年 课件 (共15张PPT)湘教版七年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第一章 有理数
1.2.3 绝对值
1.理解绝对值的概念及其几何意义.
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点 绝对值的意义
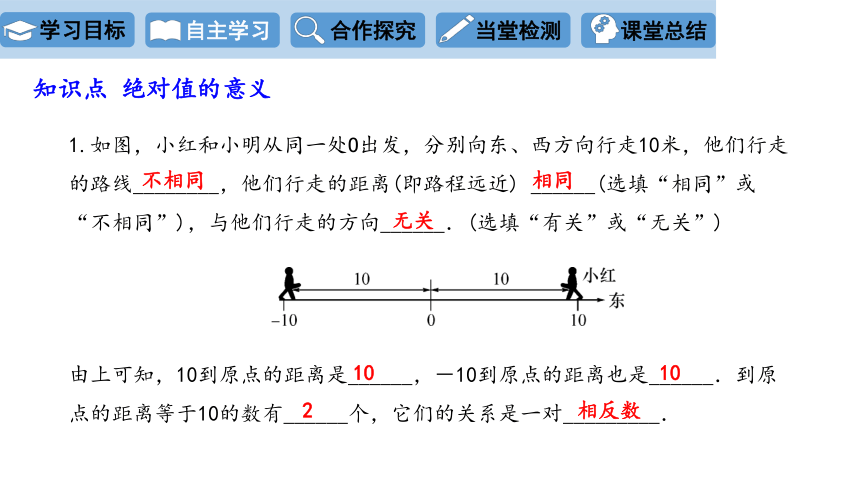
1.如图,小红和小明从同一处O出发,分别向东、西方向行走10米,他们行走的路线________,他们行走的距离(即路程远近) ______(选填“相同”或“不相同”),与他们行走的方向______.(选填“有关”或“无关”)
不相同
相同
无关
由上可知,10到原点的距离是______,-10到原点的距离也是______.到原点的距离等于10的数有______个,它们的关系是一对_________.
10
10
2
相反数
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:
1.绝对值的几何意义:一般地,数轴上表示数a的点与原点的_______叫做数a的绝对值,记作____.比如,在上面的问题中,10的绝对值是____,-10的绝对值也是____.
2.绝对值的代数意义:
(1)正数的绝对值是它____;即:当a>0时,|a|= ____;
(2)0的绝对值是____ ;即:当a=0时,|a|= ____;
(3)负数的绝对值是____________;即:当a<0时,|a|= ____.
距离
|a|
10
10
本身
a
0
0
它的相反数
-a
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 求一个数的绝对值
活动1.求下列各数的绝对值.
12, ,-7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
合作探究
当堂检测
学习目标
课堂总结
自主学习
求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
方法归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
解:
1.写出下列各数的绝对值:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 绝对值的非负性
同桌讨论:如果a表示一个数,则|a|等于多少?
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a=0时, |a|=0
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 绝对值的非负性
活动2.根据前面得出的结论,独自思考解出下面的问题,并与小组伙伴一起讨论解题的方法.
如果|x-1|=2,求x.
解:因为绝对值等于2的有理数有2和-2两个,
所以x-1=2或x-1=-2,
解得x=3或x=-1.
合作探究
当堂检测
学习目标
课堂总结
自主学习
任何一个数a的绝对值总是______的,即|a|_____0.
分情况而言:当a≠0时,|a|_____0;当a=0时,|a|_____.
非负
≥
>
=0
总结归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.(1)若|x+5|=8,那么x+5=______.
±8
练一练
(2)若|a|+|b-1|=0,则a=_____,b=_____.
0
1
【归纳】几个非负数的和为0,则这几个数都为0.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数. ( )
(2)-1.4<0,则│-1.4│<0. ( )
(3) │-32︱的相反数是32. ( )
(4) 如果两个数的绝对值相等,那么这两个数相等. ( )
(5) 互为相反数的两个数的绝对值相等. ( )
×
×
×
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
| b |=______(b<0) ;
2.化简:
-b
a-b
| 0.2 |=_____;
| a – b | =_______(a>b).
0.2
_____;
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.画一条数轴,并标出表示绝对值等于3,2.5的数的点.
-3
-2.5
3
2.5
合作探究
当堂检测
学习目标
课堂总结
自主学习
数轴上表示数a的点与原点的距离,记作|a|
性质
绝对值
概念
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
第一章 有理数
1.2.3 绝对值
1.理解绝对值的概念及其几何意义.
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点 绝对值的意义
1.如图,小红和小明从同一处O出发,分别向东、西方向行走10米,他们行走的路线________,他们行走的距离(即路程远近) ______(选填“相同”或“不相同”),与他们行走的方向______.(选填“有关”或“无关”)
不相同
相同
无关
由上可知,10到原点的距离是______,-10到原点的距离也是______.到原点的距离等于10的数有______个,它们的关系是一对_________.
10
10
2
相反数
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:
1.绝对值的几何意义:一般地,数轴上表示数a的点与原点的_______叫做数a的绝对值,记作____.比如,在上面的问题中,10的绝对值是____,-10的绝对值也是____.
2.绝对值的代数意义:
(1)正数的绝对值是它____;即:当a>0时,|a|= ____;
(2)0的绝对值是____ ;即:当a=0时,|a|= ____;
(3)负数的绝对值是____________;即:当a<0时,|a|= ____.
距离
|a|
10
10
本身
a
0
0
它的相反数
-a
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 求一个数的绝对值
活动1.求下列各数的绝对值.
12, ,-7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
合作探究
当堂检测
学习目标
课堂总结
自主学习
求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
方法归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
解:
1.写出下列各数的绝对值:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 绝对值的非负性
同桌讨论:如果a表示一个数,则|a|等于多少?
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a=0时, |a|=0
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 绝对值的非负性
活动2.根据前面得出的结论,独自思考解出下面的问题,并与小组伙伴一起讨论解题的方法.
如果|x-1|=2,求x.
解:因为绝对值等于2的有理数有2和-2两个,
所以x-1=2或x-1=-2,
解得x=3或x=-1.
合作探究
当堂检测
学习目标
课堂总结
自主学习
任何一个数a的绝对值总是______的,即|a|_____0.
分情况而言:当a≠0时,|a|_____0;当a=0时,|a|_____.
非负
≥
>
=0
总结归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.(1)若|x+5|=8,那么x+5=______.
±8
练一练
(2)若|a|+|b-1|=0,则a=_____,b=_____.
0
1
【归纳】几个非负数的和为0,则这几个数都为0.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数. ( )
(2)-1.4<0,则│-1.4│<0. ( )
(3) │-32︱的相反数是32. ( )
(4) 如果两个数的绝对值相等,那么这两个数相等. ( )
(5) 互为相反数的两个数的绝对值相等. ( )
×
×
×
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
| b |=______(b<0) ;
2.化简:
-b
a-b
| 0.2 |=_____;
| a – b | =_______(a>b).
0.2
_____;
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.画一条数轴,并标出表示绝对值等于3,2.5的数的点.
-3
-2.5
3
2.5
合作探究
当堂检测
学习目标
课堂总结
自主学习
数轴上表示数a的点与原点的距离,记作|a|
性质
绝对值
概念
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
同课章节目录
