第六单元《梯形的面积》课件(共15张PPT)五年级上册数学人教版
文档属性
| 名称 | 第六单元《梯形的面积》课件(共15张PPT)五年级上册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 685.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 07:08:58 | ||
图片预览




文档简介
(共15张PPT)
梯形的面积
人教版五年级上册
3.5cm
9.6cm
6.3cm
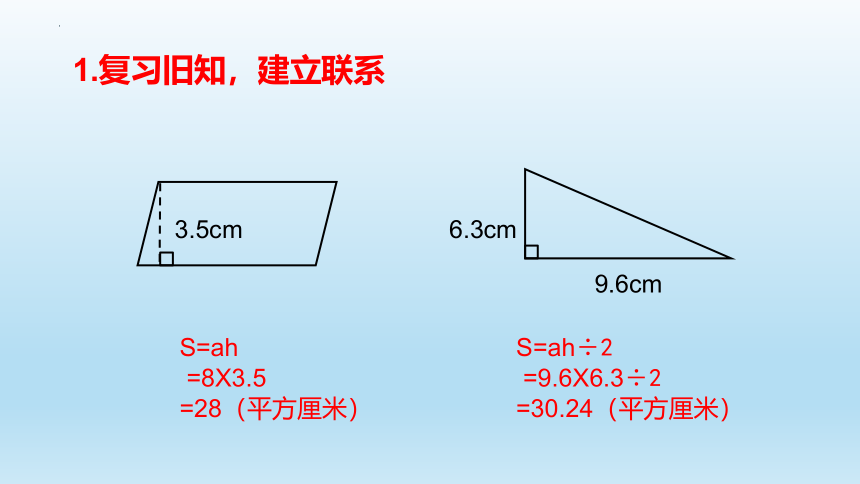
S=ah
=8X3.5
=28(平方厘米)
S=ah÷2
=9.6X6.3÷2
=30.24(平方厘米)
1.复习旧知,建立联系
2.学习新知,激发思考
1.前面我们已经学习了借助剪拼、倍拼等方法将未知图形转化为已知图形,面对梯形,你准备怎样变化,将它转化为已知图形?
2.与同桌合作开展活动,并交流想法。
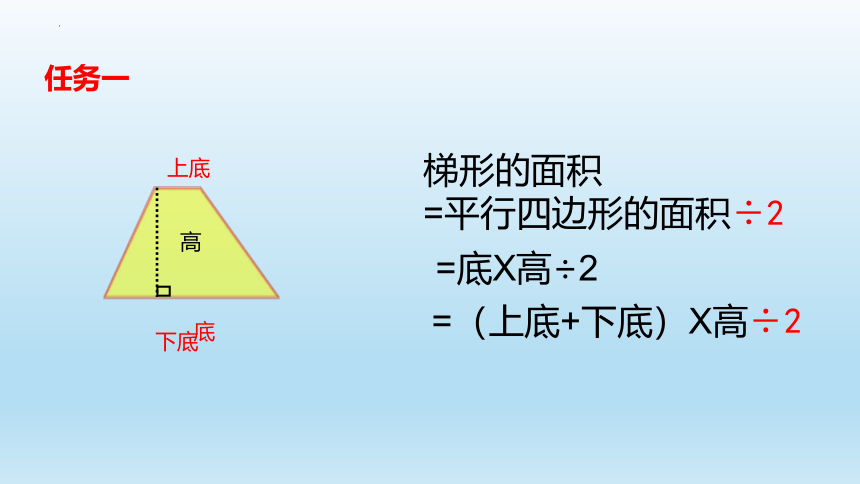
任务一
3.动手操作,合作探究
底
下底
上底
梯形的面积
=平行四边形的面积÷2
高
任务一
=(上底+下底)X高÷2
=底X高÷2
梯形的面积=
三角形面积①+三角形面积②
=下底X高÷2+上底X高÷2
=(上底+下底)X高÷2
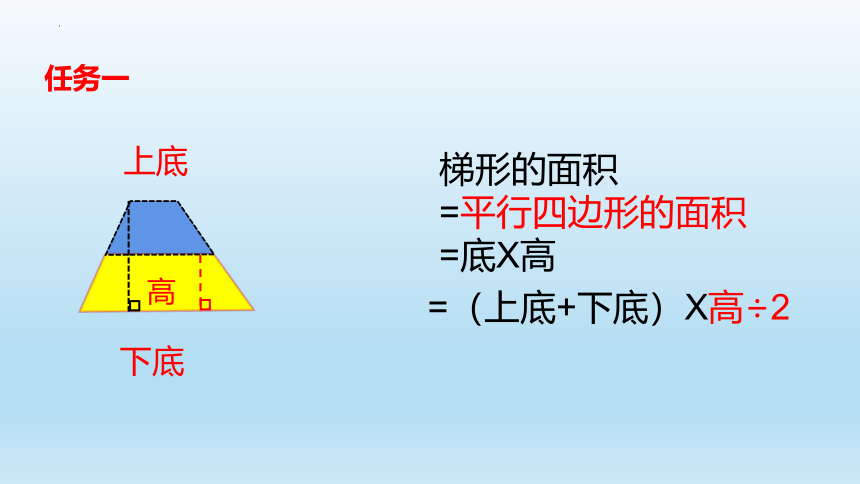
任务一
①
②
梯形的面积
=平行四边形的面积
=底X高
任务一
=(上底+下底)X高÷2
下底
上底
高
上底
高
上底
下底
下底
高
上底
下底
高
上底
下底
倍拼
分割
割补
早在古代,我国数学家刘徽就利用出入相补原理来计算平面图形的面积。出入相补原理就是把一个进行图形分割、移补,而面积保持不变,来计算出它的面积。如下图所示,它们显示了平面图形之间的转化。
上底
下底
高
4.数学文化,融入课堂
5.归纳总结,整理提升
S=(a +b)×h÷2
梯形的面积 =(上底 +下底)×高÷2
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
b
a
h
7.应用梯形面积公式解决导入问题
一块梯形的车窗玻璃,上底是45厘米,下底是75厘米,高是40厘米。
现在你会运用所学的知识来计算车窗玻璃的面积吗?
任务二
8.通过拓展作业,渗透面积之间的联系
有一个图形可以用
(3+6)X5÷2来计算,
请你在方格纸上画一画
(小正方形的边长为1CM)
设计意图:1.深入理解“等底等高”的图形间关系。
2.渗透梯形面积与平行四边形及三角形面积之间的关联。
任务三
5cm
(3+6)X5÷2
6
3
5
3
5
6
3
5
6
任务三
课后作业
基础作业:
数学书P95页T2
长周期作业:
继续补充本单元梯形面积的思维导图
梯形的面积
人教版五年级上册
3.5cm
9.6cm
6.3cm
S=ah
=8X3.5
=28(平方厘米)
S=ah÷2
=9.6X6.3÷2
=30.24(平方厘米)
1.复习旧知,建立联系
2.学习新知,激发思考
1.前面我们已经学习了借助剪拼、倍拼等方法将未知图形转化为已知图形,面对梯形,你准备怎样变化,将它转化为已知图形?
2.与同桌合作开展活动,并交流想法。
任务一
3.动手操作,合作探究
底
下底
上底
梯形的面积
=平行四边形的面积÷2
高
任务一
=(上底+下底)X高÷2
=底X高÷2
梯形的面积=
三角形面积①+三角形面积②
=下底X高÷2+上底X高÷2
=(上底+下底)X高÷2
任务一
①
②
梯形的面积
=平行四边形的面积
=底X高
任务一
=(上底+下底)X高÷2
下底
上底
高
上底
高
上底
下底
下底
高
上底
下底
高
上底
下底
倍拼
分割
割补
早在古代,我国数学家刘徽就利用出入相补原理来计算平面图形的面积。出入相补原理就是把一个进行图形分割、移补,而面积保持不变,来计算出它的面积。如下图所示,它们显示了平面图形之间的转化。
上底
下底
高
4.数学文化,融入课堂
5.归纳总结,整理提升
S=(a +b)×h÷2
梯形的面积 =(上底 +下底)×高÷2
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
b
a
h
7.应用梯形面积公式解决导入问题
一块梯形的车窗玻璃,上底是45厘米,下底是75厘米,高是40厘米。
现在你会运用所学的知识来计算车窗玻璃的面积吗?
任务二
8.通过拓展作业,渗透面积之间的联系
有一个图形可以用
(3+6)X5÷2来计算,
请你在方格纸上画一画
(小正方形的边长为1CM)
设计意图:1.深入理解“等底等高”的图形间关系。
2.渗透梯形面积与平行四边形及三角形面积之间的关联。
任务三
5cm
(3+6)X5÷2
6
3
5
3
5
6
3
5
6
任务三
课后作业
基础作业:
数学书P95页T2
长周期作业:
继续补充本单元梯形面积的思维导图
