人教A版高中数学选修4-4 平面直角坐标系和极坐标系
文档属性
| 名称 | 人教A版高中数学选修4-4 平面直角坐标系和极坐标系 |

|
|
| 格式 | zip | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-18 00:00:00 | ||
图片预览





文档简介
课件26张PPT。人教A版高中数学选修4-4 第一讲 坐标系一、平面直角坐标系
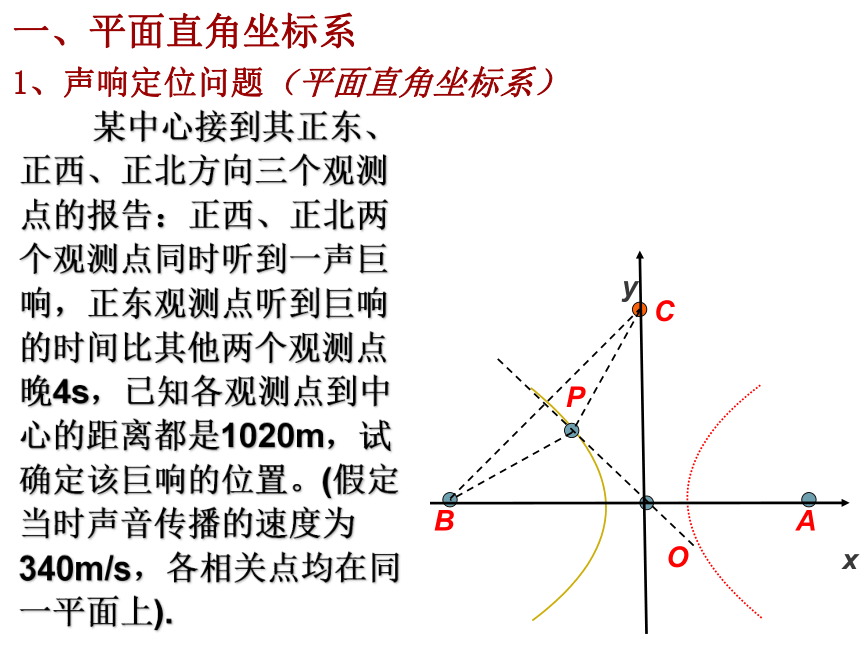
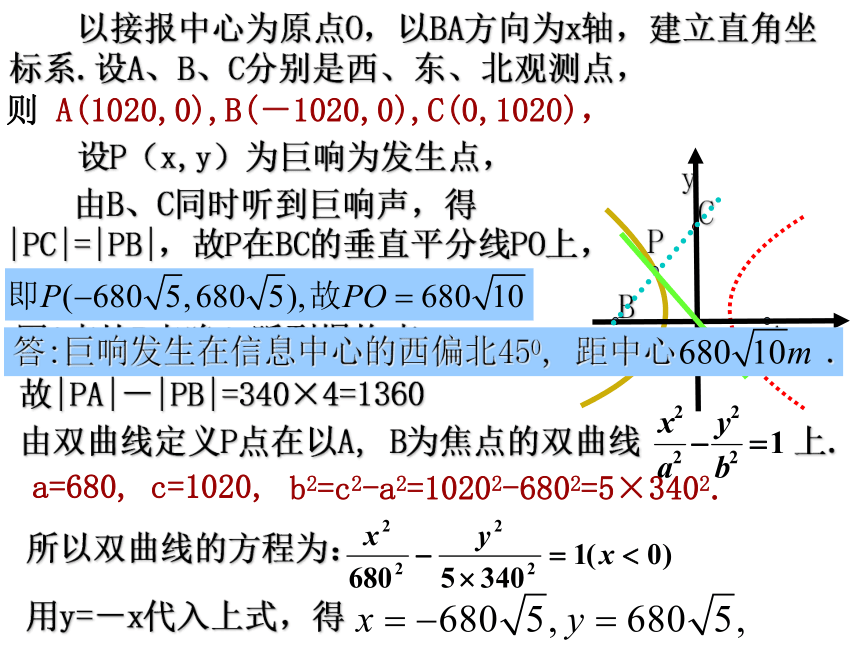
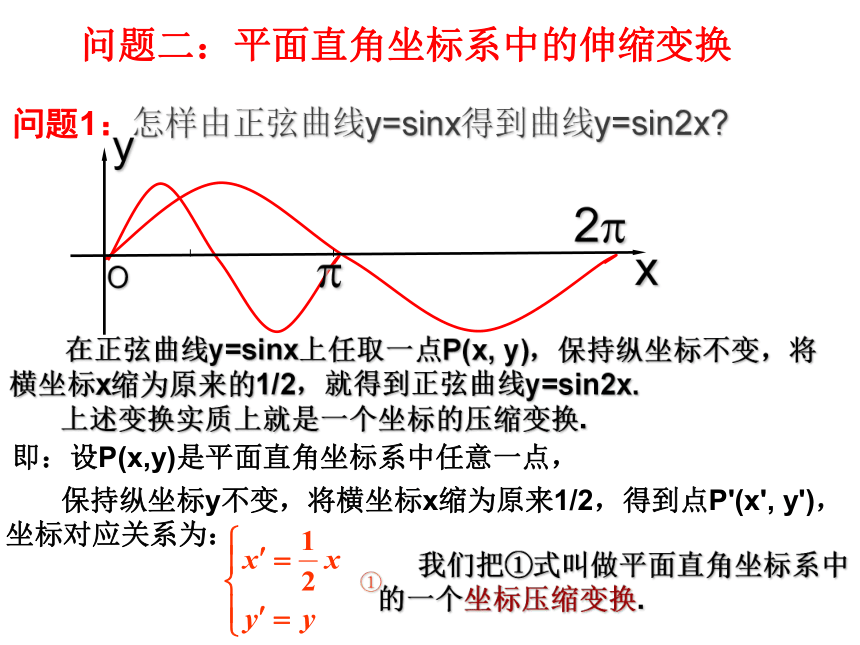
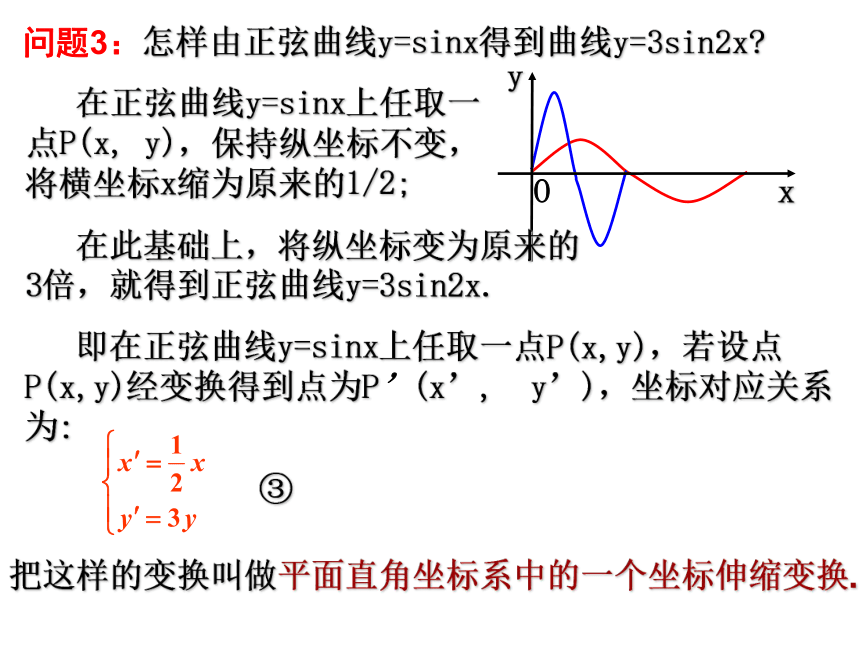
二、极坐标系一、平面直角坐标系 1、声响定位问题(平面直角坐标系) 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。(假定当时声音传播的速度为340m/s,各相关点均在同一平面上). 以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则 A(1020,0),B(-1020,0),C(0,1020), 设P(x,y)为巨响为发生点,因A点比B点晚4s听到爆炸声,故|PA|-|PB|=340×4=1360 由B、C同时听到巨响声,得|PC|=|PB|,故P在BC的垂直平分线PO上,PO的方程为y=-x,由双曲线定义P点在以A, B为焦点的双曲线 上.a=680, c=1020, b2=c2-a2=10202-6802=5×3402. 所以双曲线的方程为:用y=-x代入上式,得 一、平面直角坐标系1、声响定位问题(平面直角坐标系)坐标法(3)使图形上的特殊点尽可能多的在坐标轴上. 建系时,根据几何特点选择适当的直角坐标系,注意以下原则:(1)如果图形有对称中心,可以选对称中心为坐标原点;(2)如果图形有对称轴,可以选择对称轴为坐标轴;例1、已知△ABC的三边a, b, c满足b2+c2=5a2,BE,CF分别为边AC, CF上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系.A(0,0),B(c,0),F(c/2,0).解:以△ABC的顶点A为原点O,边AB所在的直线x轴,建立直角坐标系,由已知,点A、B、F的坐标分别为所以2x2+2y2+2c2-5cx=0.设C点坐标为(x,y),则点E的坐标为(x/2,y/2),由b2+c2=5a2,|AC|2+|AB|2=5|BC|2,即x2+y2+c2=5[(x-c)2+y2],=-(2x2+2y2+2c2-5cx)/4=0 因为=(x/2-c,y/2),所以=(c/2-x,-y),(x/2-c,y/2)·(c/2-x,-y)因此,BE与CF互相垂直.问题二:平面直角坐标系中的伸缩变换问题1:怎样由正弦曲线y=sinx得到曲线y=sin2x? 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标不变,将横坐标x缩为原来的1/2,就得到正弦曲线y=sin2x.①上述变换实质上就是一个坐标的压缩变换.即:设P(x,y)是平面直角坐标系中任意一点, 保持纵坐标y不变,将横坐标x缩为原来1/2,得到点P'(x', y'),坐标对应关系为: 我们把①式叫做平面直角坐标系中的一个坐标压缩变换.问题2:怎样由正弦曲线y=sinx得到曲线y=3sinx? 在正弦曲线上任取一点P(x, y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx.上述变换实质上就是一个坐标的伸长变换.即:设P(x,y)是平面直角坐标系中任意一点, 设P(x, y)是平面直角坐标系中任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点P'(x', y'),坐标对应关系为:②我们把②式叫做平面直角坐标系中的一个坐标伸长变换. 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标不变,将横坐标x缩为原来的1/2;问题3:怎样由正弦曲线y=sinx得到曲线y=3sin2x? 在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
即在正弦曲线y=sinx上任取一点P(x,y),若设点P(x,y)经变换得到点为P’(x’, y’),坐标对应关系为: ③。把这样的变换叫做平面直角坐标系中的一个坐标伸缩变换. 设P(x, y)是平面直角坐标系中任意一点,在变换:的作用下,点P(x, y) 对应P'(x',y').称 为平面直角坐标系中的伸缩变换. 上述①②③都是坐标伸缩变换,在它们的作用下,可以实现平面图形的伸缩. ③在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。 ②把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;①2、平面直角坐标系中的伸缩变换例2、在直角坐标系中,求下列方程所对应的图形经过伸缩变换:后的图形.(1)2x+3y=0;(2)x2+y2=1.,代入2x+3y=0;; 得到经过伸缩变换后的图形的方程是得到经过伸缩变换后的图形的方程是目标检测:3、将点(2,3)变成点(3,2)的伸缩变换是( ) 下图是某校园的平面示意图.假设某
同学在教学楼处,请回答下列问题:
(1)他向东偏北60o方向走120m后
到达什么位置?
该位置惟一确定吗?
(2)如果有人打听
体育馆和办公楼的位
置,他应如何描述?AEBCD60o45o办公楼实验楼图书馆体育馆120m60m教学楼50m二、极坐标系 在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。1、极坐标系的建立在平面内取一个定点O,叫做极点。引一条射线Ox,叫做极轴。 再选定一个长度单位和角度单位及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。O2、极坐标系内一点的极坐标的规定 对于平面上任意一点M,用?表示线段OM的长度, 用?表示从OX到OM 的角度, ?叫做点M的极径,?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。(2)当M在极点时,它的极坐标为(0,θ),?可取任意值.例2、在图中,用点A,B,C,D,E
分别表示教学楼,体育馆,图书馆,
实验楼,办公楼的位置.建立适当的
极坐标系,写出各点的极坐标.AEBCD60o45o120m60m50mA(O)x 极坐标(?,?)与(?,?+2k?)(k∈Z)表示同一个点.特别地,极点O的坐标为(0,?)
(? ∈R).和直角坐标不同,平面内一个
点的极坐标有无数种表示. 如果规定?>0,0≤?<2?,那么除
极点外,平面内的点可用惟一的极坐标
(?,?)表示;同时,极坐标表示的点(?,?)
也是惟一确定的.二、极坐标系3、极坐标和直角坐标的互化思考:平面内的一个点既可以用直角坐标表示,也可以用极坐标表示.那么,这两种坐标之间有什么关系呢? 把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位. 设M是平面内任意一点,它的直角坐标是(x,y)极坐标是(?,?).
从下图可以得出它们之间的关系:NxxyMOy??由①又可得到下面的关系式:3、极坐标和直角坐标的互化设点M的直角坐标是(x,y),极坐标是(ρ,θ)x=ρcosθ, y=ρsinθ极坐标转化为直角坐标:直角坐标转化为极坐标:例3、将点M的极坐标 化成直角坐标.解: 所以, 点M的直角坐标为∵点M的直角坐标为解:设点M的极坐标为(ρ,θ)例4、平面内的一点M的直角坐标为(1, ),则点M如何用极坐标表示?oxP1P2推广:从这向北
2000米。请问:去菜
市场怎么走?请分析上面这句话,他告诉了问路人什么?从这向北走2000米!出发点方向距离 在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。谢谢观赏WPS OfficeMake Presentation much more fun@WPS官方微博
@kingsoftwps
二、极坐标系一、平面直角坐标系 1、声响定位问题(平面直角坐标系) 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。(假定当时声音传播的速度为340m/s,各相关点均在同一平面上). 以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则 A(1020,0),B(-1020,0),C(0,1020), 设P(x,y)为巨响为发生点,因A点比B点晚4s听到爆炸声,故|PA|-|PB|=340×4=1360 由B、C同时听到巨响声,得|PC|=|PB|,故P在BC的垂直平分线PO上,PO的方程为y=-x,由双曲线定义P点在以A, B为焦点的双曲线 上.a=680, c=1020, b2=c2-a2=10202-6802=5×3402. 所以双曲线的方程为:用y=-x代入上式,得 一、平面直角坐标系1、声响定位问题(平面直角坐标系)坐标法(3)使图形上的特殊点尽可能多的在坐标轴上. 建系时,根据几何特点选择适当的直角坐标系,注意以下原则:(1)如果图形有对称中心,可以选对称中心为坐标原点;(2)如果图形有对称轴,可以选择对称轴为坐标轴;例1、已知△ABC的三边a, b, c满足b2+c2=5a2,BE,CF分别为边AC, CF上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系.A(0,0),B(c,0),F(c/2,0).解:以△ABC的顶点A为原点O,边AB所在的直线x轴,建立直角坐标系,由已知,点A、B、F的坐标分别为所以2x2+2y2+2c2-5cx=0.设C点坐标为(x,y),则点E的坐标为(x/2,y/2),由b2+c2=5a2,|AC|2+|AB|2=5|BC|2,即x2+y2+c2=5[(x-c)2+y2],=-(2x2+2y2+2c2-5cx)/4=0 因为=(x/2-c,y/2),所以=(c/2-x,-y),(x/2-c,y/2)·(c/2-x,-y)因此,BE与CF互相垂直.问题二:平面直角坐标系中的伸缩变换问题1:怎样由正弦曲线y=sinx得到曲线y=sin2x? 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标不变,将横坐标x缩为原来的1/2,就得到正弦曲线y=sin2x.①上述变换实质上就是一个坐标的压缩变换.即:设P(x,y)是平面直角坐标系中任意一点, 保持纵坐标y不变,将横坐标x缩为原来1/2,得到点P'(x', y'),坐标对应关系为: 我们把①式叫做平面直角坐标系中的一个坐标压缩变换.问题2:怎样由正弦曲线y=sinx得到曲线y=3sinx? 在正弦曲线上任取一点P(x, y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx.上述变换实质上就是一个坐标的伸长变换.即:设P(x,y)是平面直角坐标系中任意一点, 设P(x, y)是平面直角坐标系中任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点P'(x', y'),坐标对应关系为:②我们把②式叫做平面直角坐标系中的一个坐标伸长变换. 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标不变,将横坐标x缩为原来的1/2;问题3:怎样由正弦曲线y=sinx得到曲线y=3sin2x? 在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
即在正弦曲线y=sinx上任取一点P(x,y),若设点P(x,y)经变换得到点为P’(x’, y’),坐标对应关系为: ③。把这样的变换叫做平面直角坐标系中的一个坐标伸缩变换. 设P(x, y)是平面直角坐标系中任意一点,在变换:的作用下,点P(x, y) 对应P'(x',y').称 为平面直角坐标系中的伸缩变换. 上述①②③都是坐标伸缩变换,在它们的作用下,可以实现平面图形的伸缩. ③在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。 ②把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;①2、平面直角坐标系中的伸缩变换例2、在直角坐标系中,求下列方程所对应的图形经过伸缩变换:后的图形.(1)2x+3y=0;(2)x2+y2=1.,代入2x+3y=0;; 得到经过伸缩变换后的图形的方程是得到经过伸缩变换后的图形的方程是目标检测:3、将点(2,3)变成点(3,2)的伸缩变换是( ) 下图是某校园的平面示意图.假设某
同学在教学楼处,请回答下列问题:
(1)他向东偏北60o方向走120m后
到达什么位置?
该位置惟一确定吗?
(2)如果有人打听
体育馆和办公楼的位
置,他应如何描述?AEBCD60o45o办公楼实验楼图书馆体育馆120m60m教学楼50m二、极坐标系 在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。1、极坐标系的建立在平面内取一个定点O,叫做极点。引一条射线Ox,叫做极轴。 再选定一个长度单位和角度单位及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。O2、极坐标系内一点的极坐标的规定 对于平面上任意一点M,用?表示线段OM的长度, 用?表示从OX到OM 的角度, ?叫做点M的极径,?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。(2)当M在极点时,它的极坐标为(0,θ),?可取任意值.例2、在图中,用点A,B,C,D,E
分别表示教学楼,体育馆,图书馆,
实验楼,办公楼的位置.建立适当的
极坐标系,写出各点的极坐标.AEBCD60o45o120m60m50mA(O)x 极坐标(?,?)与(?,?+2k?)(k∈Z)表示同一个点.特别地,极点O的坐标为(0,?)
(? ∈R).和直角坐标不同,平面内一个
点的极坐标有无数种表示. 如果规定?>0,0≤?<2?,那么除
极点外,平面内的点可用惟一的极坐标
(?,?)表示;同时,极坐标表示的点(?,?)
也是惟一确定的.二、极坐标系3、极坐标和直角坐标的互化思考:平面内的一个点既可以用直角坐标表示,也可以用极坐标表示.那么,这两种坐标之间有什么关系呢? 把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位. 设M是平面内任意一点,它的直角坐标是(x,y)极坐标是(?,?).
从下图可以得出它们之间的关系:NxxyMOy??由①又可得到下面的关系式:3、极坐标和直角坐标的互化设点M的直角坐标是(x,y),极坐标是(ρ,θ)x=ρcosθ, y=ρsinθ极坐标转化为直角坐标:直角坐标转化为极坐标:例3、将点M的极坐标 化成直角坐标.解: 所以, 点M的直角坐标为∵点M的直角坐标为解:设点M的极坐标为(ρ,θ)例4、平面内的一点M的直角坐标为(1, ),则点M如何用极坐标表示?oxP1P2推广:从这向北
2000米。请问:去菜
市场怎么走?请分析上面这句话,他告诉了问路人什么?从这向北走2000米!出发点方向距离 在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。谢谢观赏WPS OfficeMake Presentation much more fun@WPS官方微博
@kingsoftwps
