对数函数(山东省东营市垦利县)
文档属性
| 名称 | 对数函数(山东省东营市垦利县) |

|
|
| 格式 | rar | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-07 00:00:00 | ||
图片预览


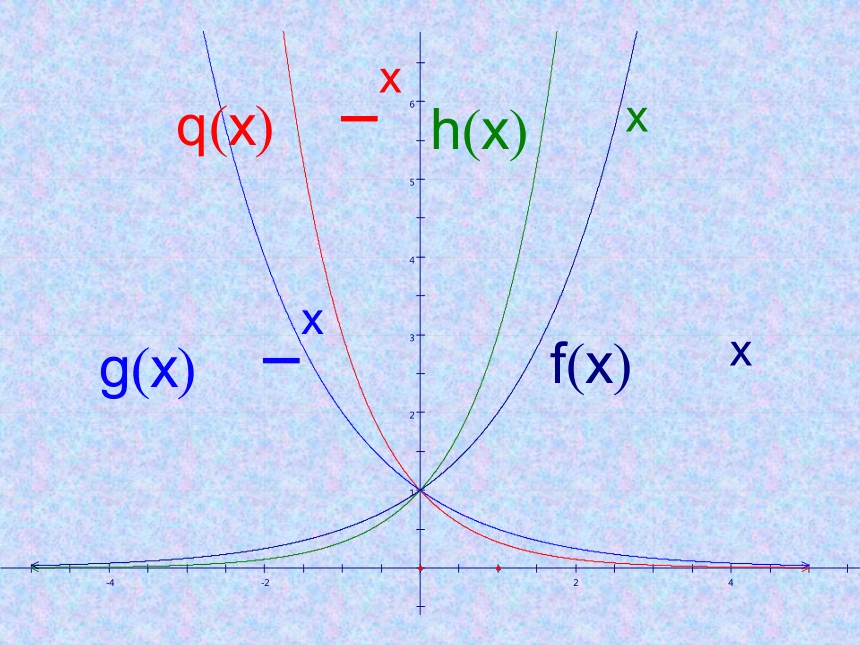




文档简介
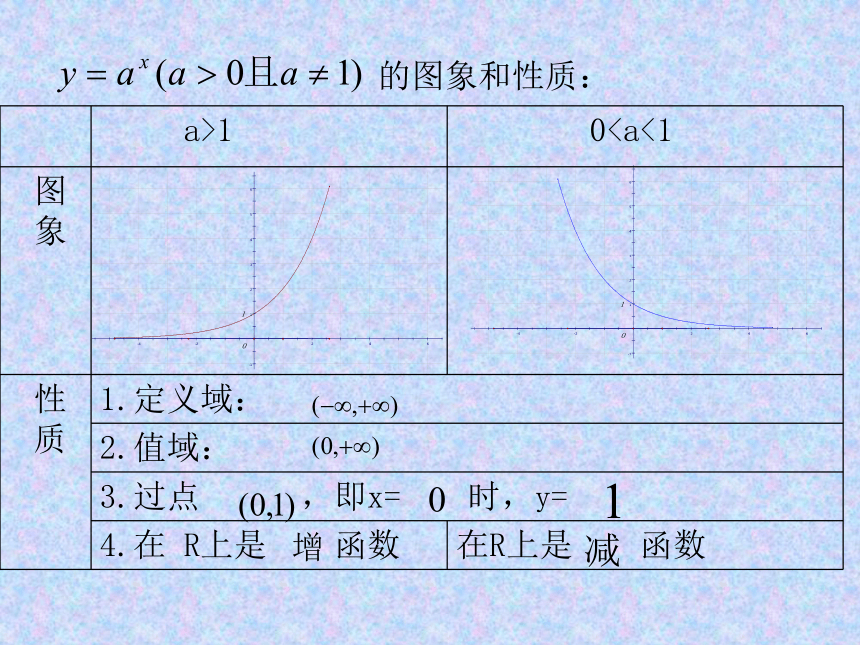
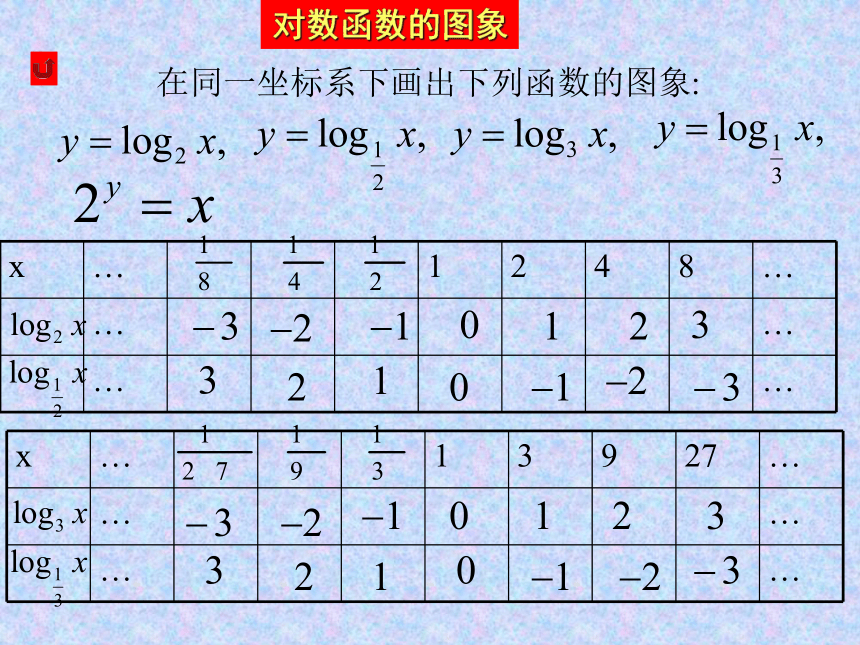
课件22张PPT。课题: 对 数 函 数垦利一中高一数学组复习引入1、问题回顾:指数函数:y=ax (a>0且a≠1)我们是怎样研究指数函数的图象和性质的?它们的图象性质如何?的图象和性质: 复习引入2、提出问题 ⑴问题回顾:某种细胞分裂时,由1个分裂成2个,2个分裂成4,……,一个这样的细胞分裂x次后,得到的细胞个数y与分裂次数x的函数关系式是:y=2x ⑵相反的问题:若一个细胞分裂后的个数为2,4,8 ……y个,分裂次数是多少?得到细胞分裂次数x关于细胞个数y的函数关系式是x=㏒2y习惯上表示为: y=㏒2x 这样的函数称为对数函数。对数函数定义一般地,当a>0且a≠1时形如y=logax 的函数叫做对数函数对数函数的定义域是(0,+∞),值域是R。对数函数的图象在同一坐标系下画出下列函数的图象:图
象解析式对数函数 1、? 定义域是 2、 值域是 3 、 过定点 性
质5、在(0,+∞)上
是 函数 5、在(0,+∞)上
是 函数xy(a>1)xy(0 当0<x<1, 4、当x>1,
当0<x<1, y>0y<0y<0y>0 oo应用举例1.比较大小(1)(2)(3)(4)(5)应用举例2.解下列各式中x的范围(1)(2)(3)(4)变式练习:求下列函数的定义域:
⑴ ⑵
⑶
解:(1)∵x2 > 0∴x≠0 (2)∵4―x>0 ∴x<4
∴函数的定义域是{x∣x<4}( 3 ) ∵9―x2>0
∴―3 ∴函数的定义域是{x∣―3象解析式对数函数 1、? 定义域是 2、 值域是 3 、 过定点 性
质5、在(0,+∞)上
是 函数 5、在(0,+∞)上
是 函数xy(a>1)xy(0 当0<x<1, 4、当x>1,
当0<x<1, y>0y<0y<0y>0 oo
函数定义域的要求
⑴若f(x)是分式,则分母不为0⑵若f(x)是偶次根式,则被开方式≥0 ⑶若f(x)=a0,则a ≠0⑷若f(x)是对数函数,则真数>0⑸若f(x)是由几个部分的数学式子构成的,则函 数的定义域是使各部分都有意义的实数集合2、必须使实际问题有意义小结(二)1、必须使函数式有意义 ∴ 2 < x ≤ 4
∴函数的定义域是{x∣2即 x > 1
x ―1 > 1
x≤4
即 x>1
㏒ 2 ( x ―1) > ㏒ 2 1
解 4-x ≥0
∵ x ―1 > 0
㏒ 2 ( x ―1) > 0
< x ≤4
∴ x > 1
x > 2
< ∴ 1< x <2
∴函数的定义域是{x∣1∴所求函数的定义域是{x∣-10且a 1,比较
应用举例解:
应用举例应用举例
应用举例(1)求定义域,单调区间(2)求f(x)的最大值,并求出取得最大值时的x的值。指数函数的图象和性质: 增减8y=log2xy=lgxy=log1/2x一般地,函数y=logax (a>0且a≠1)的图象怎么样呢?
象解析式对数函数 1、? 定义域是 2、 值域是 3 、 过定点 性
质5、在(0,+∞)上
是 函数 5、在(0,+∞)上
是 函数xy(a>1)xy(0
当0<x<1, y>0y<0y<0y>0 oo应用举例1.比较大小(1)(2)(3)(4)(5)应用举例2.解下列各式中x的范围(1)(2)(3)(4)变式练习:求下列函数的定义域:
⑴ ⑵
⑶
解:(1)∵x2 > 0∴x≠0 (2)∵4―x>0 ∴x<4
∴函数的定义域是{x∣x<4}( 3 ) ∵9―x2>0
∴―3
质5、在(0,+∞)上
是 函数 5、在(0,+∞)上
是 函数xy(a>1)xy(0
当0<x<1, y>0y<0y<0y>0 oo
函数定义域的要求
⑴若f(x)是分式,则分母不为0⑵若f(x)是偶次根式,则被开方式≥0 ⑶若f(x)=a0,则a ≠0⑷若f(x)是对数函数,则真数>0⑸若f(x)是由几个部分的数学式子构成的,则函 数的定义域是使各部分都有意义的实数集合2、必须使实际问题有意义小结(二)1、必须使函数式有意义 ∴ 2 < x ≤ 4
∴函数的定义域是{x∣2
x ―1 > 1
x≤4
即 x>1
㏒ 2 ( x ―1) > ㏒ 2 1
解 4-x ≥0
∵ x ―1 > 0
㏒ 2 ( x ―1) > 0
< x ≤4
∴ x > 1
x > 2
< ∴ 1< x <2
∴函数的定义域是{x∣1
应用举例解:
应用举例应用举例
应用举例(1)求定义域,单调区间(2)求f(x)的最大值,并求出取得最大值时的x的值。指数函数的图象和性质: 增减8y=log2xy=lgxy=log1/2x一般地,函数y=logax (a>0且a≠1)的图象怎么样呢?
