指数函数

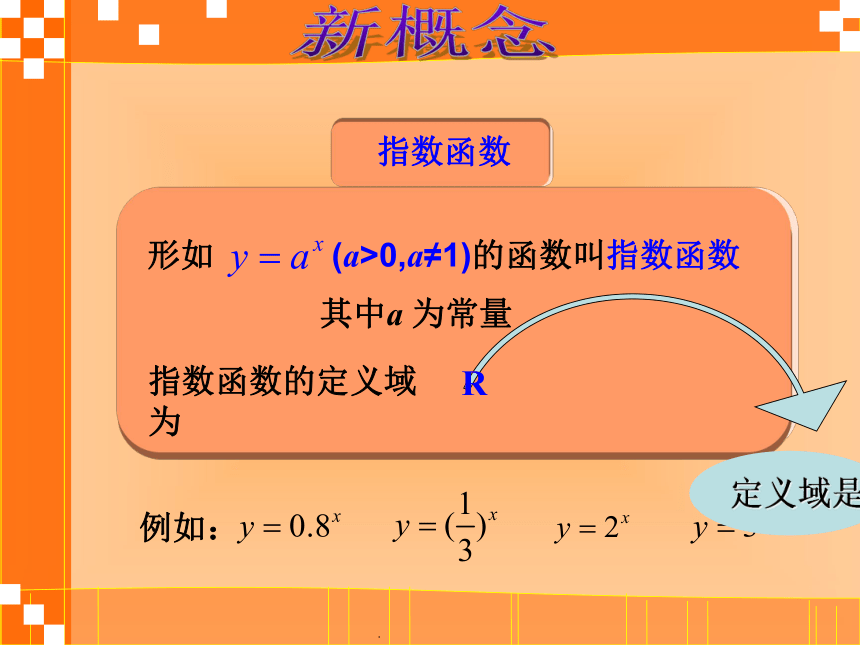
课件22张PPT。指数函数讲故事教材P84页 把一张厚度为1毫米的纸对折42次后，这张纸的厚度将达到多少？ 答案：约439.8万公里。(地球到月球的距离为38.4万公里)那么，假设厚度为1，对折x次后呢？你知道吗？新概念.形如(a>0,a≠1)的函数叫指数函数指数函数指数函数的定义域为其中a 为常量例如：问题1：为什么要规定a>0,且a≠1？如果不这样规定会出现以下情况：
当a=0时 若x﹥0，则ax ≡0；若x﹤意义0，则ax意义。
当a﹤0时 不一定有意义。
当a=1时 y=1x =1是常量。
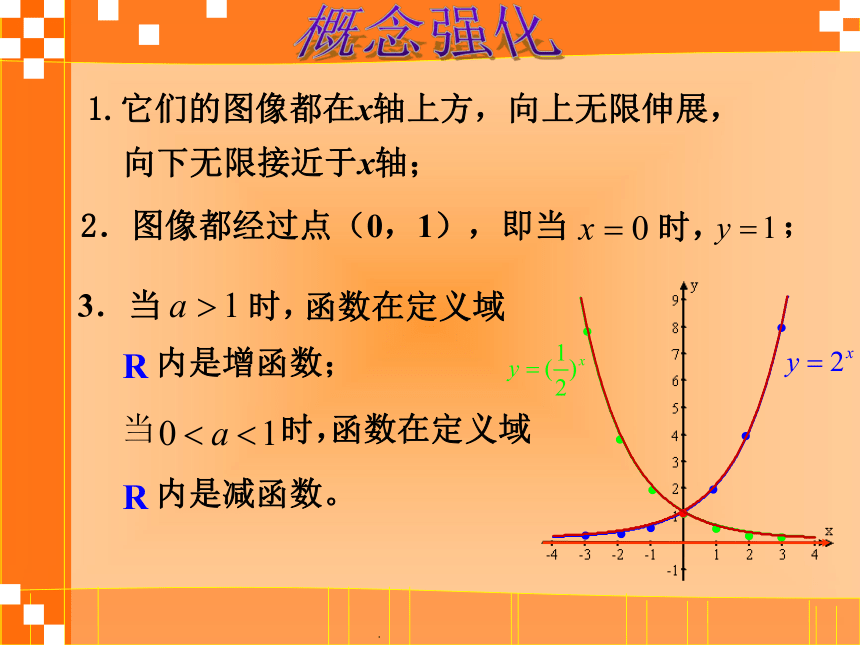
因此为了避免上述的情况，并保证定义域 是全体实数，我们规定a﹥ 0,且a≠1。2.函数 y = ( a2 - 3a + 3) ax 是指数函数，求 a的值.∴ a = 2D01122xy43-1-23-3作出函数图像：1。列表 2。描点 3。连线y=2xy= 2- x 概念强化.1.它们的图像都在x轴上方，向上无限伸展，2．图像都经过点（0，1），即当时，； 3．当内是增函数； 函数在定义域当时，时，内是减函数。 函数在定义域 向下无限接近于x轴； 概念强化.指数函数性质（1）图像都经过点（0，1）（3）当内是增函数, 函数在当内是减函数, 函数在（2）函数的定义域是R,值域是 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010(a>1)yx(0,1)y=10y=ax
(010 时，y > 1.当 x < 时，y > 1；当 x > 时，0＜y < 1 。指数函数:y=ax(a >0且a=1)0000概念强化.例1 判断下列函数在（?∞，+∞）内是增函数，
还是减函数？（1）（2）解:（3）（1）因为4>1，所以函数在（?∞，+∞）内是增函数； （2）因为，所以函数在（?∞，+∞）内是减函数； （3）由于，并且所以函数在(?∞，+∞）内是增函数． 巩固练习.1.判断下列函数在(?∞，+∞）内的单调性？ （1）（2）（3）（4）（1）增函数； （2）减函数；(3）减函数； （4）增函数.01xy试分析上述图像中，哪一条是 的图像
哪一条是 的图像y=2xy=3x例2.23101xy试分析上述图像中，哪一条是 的图像
哪一条是 的图像y= 2-xy=3-x练习 . .③④巩固练习.. 2．利用指数函数的单调性，比较下列各式中的大小.① ② ③ ① ② ③ 话说猪八戒西天取经，获得不菲奖金,创立了高老庄集团。但天有不测风云，八戒的高老庄集团经济资金周转不灵，
这时八戒向悟空求援。悟空答应每天给八戒投资10万元，连续一个月（31天）。但天上不可能掉馅饼，悟空向八戒提出了如下条件：
第一天返还1分
第二天返还2分
……..
后一天返还数为前一天的2倍。
八戒想：第一天出1分入10万元
第二天出2分入10万元
第三天出4分入10万元
感觉很合算。但八戒毕竟在商界摸爬滚打多年，心想得请高手算一算，不能又被悟空算计。请你帮八戒算算这笔帐，八戒是赔了还是赚了。第一次第二次第三次第x次…2个4个8个．．．．．．2x
个细胞个数和分裂次数 的函数 关系： Y=2x
一、观察实例------细胞的分裂过程