3.4 一元一次方程(浙江省台州市仙居县)
文档属性
| 名称 | 3.4 一元一次方程(浙江省台州市仙居县) |  | |
| 格式 | rar | ||
| 文件大小 | 860.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-06 08:28:00 | ||
图片预览






文档简介
课件17张PPT。 3.4 一元一次方程
解决实际问题 学识目标: 1.能用方程解决实际问题
2.明确用方程解决实际问题
的一般思路和步骤
3.建立自己数学模型思想1.解下列方程:
(1)12(x+1)= -(3x-1);
(2) 2(y-3)-3(2+y)=0;
(3) 2-3(m-1)= m+1;
(4)3(2x-3)-3[3(2x-3)+3]=5.
热身练习: 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时.已知水流的速度是3千米/时,求船在静水中的平均速度. 问题1:此题已知什么? 求什么?问题2:此题中的相等关系是______________往返的路程相等问题3:如果设船在静水中的平均速度为x千米/小时,那么船在顺水时的速度为______千米/小时,在逆流的速度为______千米/小时.(x+3)(x-3)顺水的速度=静水中的速度+水流的速度
逆水的速度=静水中的速度–水流的速度 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时.已知水流的速度是3千米/时,求船在静水中的平均速度. 解:设船在静水中的平均速度为x千米/时,则列方程得:
2(x+3)=2.5(x-3).
去括号,得 2x+6=2.5x-7.5
移项,得 2x - 2.5x =-7.5 -6
合并,得 - 0.5x= - 13.5
系数化为1,得 x=27
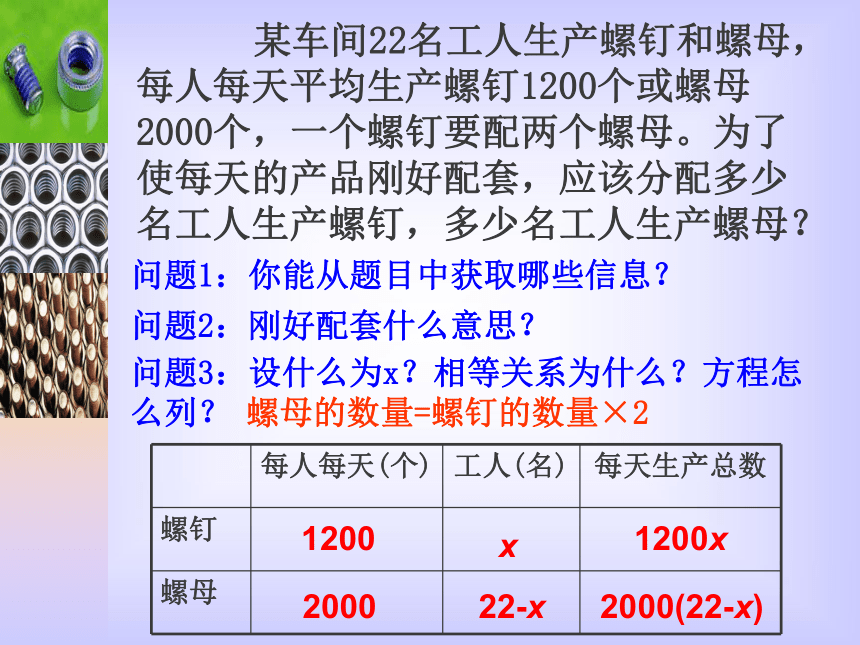
答:船在静水中的平均速度为27千米/时. 某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母。为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?问题1:你能从题目中获取哪些信息?问题2:刚好配套什么意思?问题3:设什么为x?相等关系为什么?方程怎么列?螺母的数量=螺钉的数量×21200x1200x200022-x2000(22-x) 如果设x人生产螺母,怎样列、解方程?解:设生产螺母的人数为x人,则生产螺钉的
人数为 (22-x) 人。列方程得:
2×1200 (22-x)=2000x
即 2400 (22-x)=2000x
去括号,得 52800-2400 x=2000x
移项,得 -2400 x-2000x= - 52800
合并,得 -4400x= - 52800
系数化为1,得 x=12
所以,生产螺钉人数为22- x=22-12=10(名)
答:应分配10名工人生产螺钉,12名工人生产螺母。 某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?挖出的土方数=运走的土方数试一试 用白铁皮做罐头盒,每张铁片可制盒身10个或制盒底30个。一个盒身与两个盒底配成一套罐头盒。现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分利用白铁皮?盒身的个数×2=盒底的个数试一试 小明在静水中划船的速度为每小时12千米,今往返于某河,逆流时用了10小时,顺流时用了6小时.
根据上面的事实,提出问题并尝试解答.考考你: 通过这节课的学习你获得了哪些新的知识?
在学习方法上有什么收获?
在解决配套、分配等问题方面你获得了哪些经验?这些问题中的相等关系有什么特点?课堂回顾:你学到了什么方程的解一般步骤实际问题抽象数学问题分析已知量、未知
量、相等关系列出方程求出验证解的合理性不合理合理解释作业本(一)
每课一练P36(二)
数学作文:
展开你想象的翅膀,运用我们今天所学的知识,根据方程:
2(x+0.5)+3x=95
编写一道应用题,并补全它的解题过程。作业: 用如图1的长方形和正方形纸板作侧面和底面,做成如图2竖式和横式的两种无盖纸盒,现在仓库里有1 000张正方形纸板和2 000张长方形纸板,问两种纸盒各做多少只,恰好使库存的纸板用完?图 1图 2等量关系是什么?5 0 01001某车间每天能生产甲种零件75个,或乙种零件100个。甲、乙两种零件分别取3个、2个才能配成一套,要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数?
思考题:用20张白卡纸做包装盒,每张白卡纸可以做盒身两个,或者做盒底盖3个.如果一个盒身和两个底盖可以做成一个包装盒,那么能否把这白卡纸分成两部分,一部分做盒身,一部分做底盖,使做成的盒身和盒底盖正好配套? 请设计一种分法,既能使盒身和盒底配套,又能充分利用白纸卡. 再见世上无难事,只要肯攀登!
解决实际问题 学识目标: 1.能用方程解决实际问题
2.明确用方程解决实际问题
的一般思路和步骤
3.建立自己数学模型思想1.解下列方程:
(1)12(x+1)= -(3x-1);
(2) 2(y-3)-3(2+y)=0;
(3) 2-3(m-1)= m+1;
(4)3(2x-3)-3[3(2x-3)+3]=5.
热身练习: 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时.已知水流的速度是3千米/时,求船在静水中的平均速度. 问题1:此题已知什么? 求什么?问题2:此题中的相等关系是______________往返的路程相等问题3:如果设船在静水中的平均速度为x千米/小时,那么船在顺水时的速度为______千米/小时,在逆流的速度为______千米/小时.(x+3)(x-3)顺水的速度=静水中的速度+水流的速度
逆水的速度=静水中的速度–水流的速度 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时.已知水流的速度是3千米/时,求船在静水中的平均速度. 解:设船在静水中的平均速度为x千米/时,则列方程得:
2(x+3)=2.5(x-3).
去括号,得 2x+6=2.5x-7.5
移项,得 2x - 2.5x =-7.5 -6
合并,得 - 0.5x= - 13.5
系数化为1,得 x=27
答:船在静水中的平均速度为27千米/时. 某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母。为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?问题1:你能从题目中获取哪些信息?问题2:刚好配套什么意思?问题3:设什么为x?相等关系为什么?方程怎么列?螺母的数量=螺钉的数量×21200x1200x200022-x2000(22-x) 如果设x人生产螺母,怎样列、解方程?解:设生产螺母的人数为x人,则生产螺钉的
人数为 (22-x) 人。列方程得:
2×1200 (22-x)=2000x
即 2400 (22-x)=2000x
去括号,得 52800-2400 x=2000x
移项,得 -2400 x-2000x= - 52800
合并,得 -4400x= - 52800
系数化为1,得 x=12
所以,生产螺钉人数为22- x=22-12=10(名)
答:应分配10名工人生产螺钉,12名工人生产螺母。 某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?挖出的土方数=运走的土方数试一试 用白铁皮做罐头盒,每张铁片可制盒身10个或制盒底30个。一个盒身与两个盒底配成一套罐头盒。现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分利用白铁皮?盒身的个数×2=盒底的个数试一试 小明在静水中划船的速度为每小时12千米,今往返于某河,逆流时用了10小时,顺流时用了6小时.
根据上面的事实,提出问题并尝试解答.考考你: 通过这节课的学习你获得了哪些新的知识?
在学习方法上有什么收获?
在解决配套、分配等问题方面你获得了哪些经验?这些问题中的相等关系有什么特点?课堂回顾:你学到了什么方程的解一般步骤实际问题抽象数学问题分析已知量、未知
量、相等关系列出方程求出验证解的合理性不合理合理解释作业本(一)
每课一练P36(二)
数学作文:
展开你想象的翅膀,运用我们今天所学的知识,根据方程:
2(x+0.5)+3x=95
编写一道应用题,并补全它的解题过程。作业: 用如图1的长方形和正方形纸板作侧面和底面,做成如图2竖式和横式的两种无盖纸盒,现在仓库里有1 000张正方形纸板和2 000张长方形纸板,问两种纸盒各做多少只,恰好使库存的纸板用完?图 1图 2等量关系是什么?5 0 01001某车间每天能生产甲种零件75个,或乙种零件100个。甲、乙两种零件分别取3个、2个才能配成一套,要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数?
思考题:用20张白卡纸做包装盒,每张白卡纸可以做盒身两个,或者做盒底盖3个.如果一个盒身和两个底盖可以做成一个包装盒,那么能否把这白卡纸分成两部分,一部分做盒身,一部分做底盖,使做成的盒身和盒底盖正好配套? 请设计一种分法,既能使盒身和盒底配套,又能充分利用白纸卡. 再见世上无难事,只要肯攀登!
