2023-2024学年苏科版数学九年级下册第6章图形的相似单元测试题(含答案)
文档属性
| 名称 | 2023-2024学年苏科版数学九年级下册第6章图形的相似单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 16:23:10 | ||
图片预览


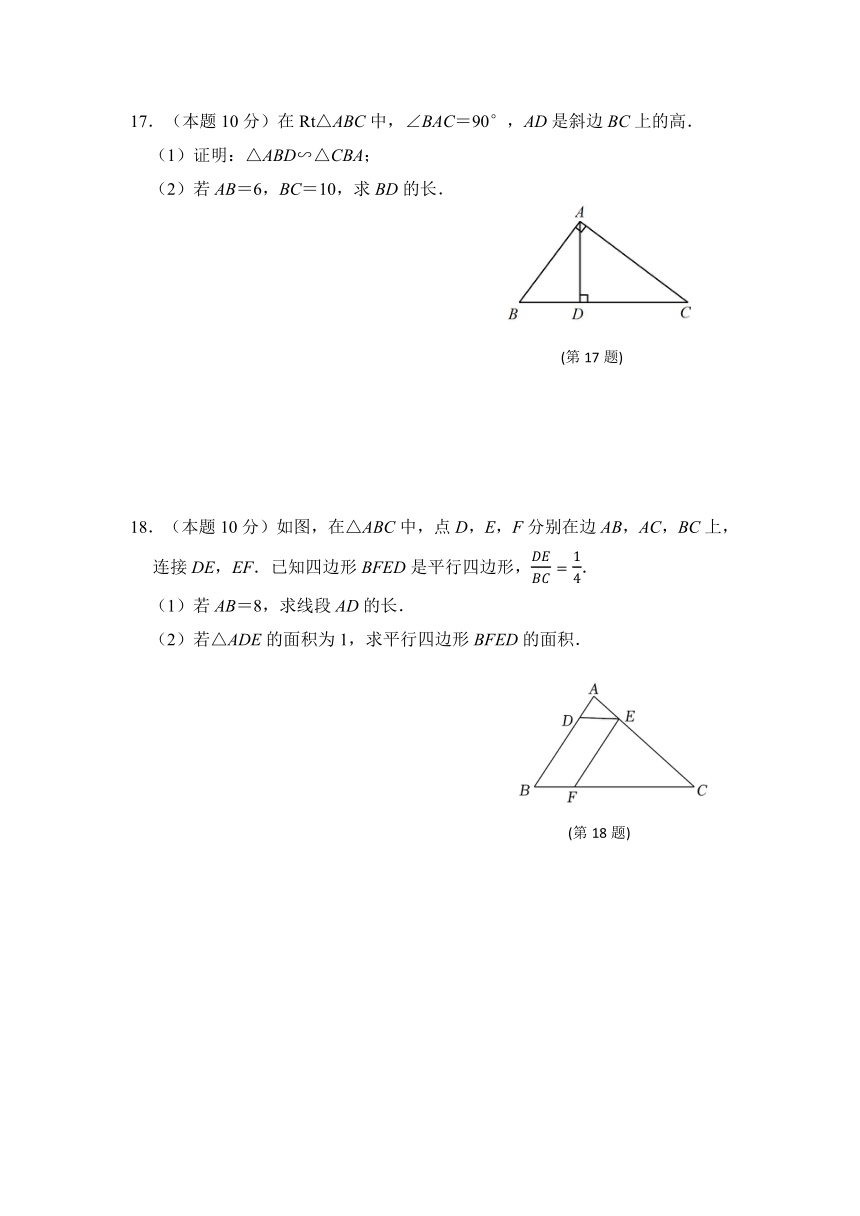
文档简介
图形的相似单元测试题
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.若,则ab=( )
A.6 B. C.1 D.
2.(2023 吉林)如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是( )
A. B. C. D.
3.(2023 重庆)若两个相似三角形周长的比为1:4,则这两个三角形对应边的比是( )
A.1:2 B.1:4 C.1:8 D.1:16
4.(2023 东营)如图,△ABC为等边三角形,点D,E分别在边BC,AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
A.1.8 B.2.4 C.3 D.3.2
5.(2023 绵阳)黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形.若CF=4a,则AB=( )
A.(1)a B.(2)a C.(1)a D.(2)a
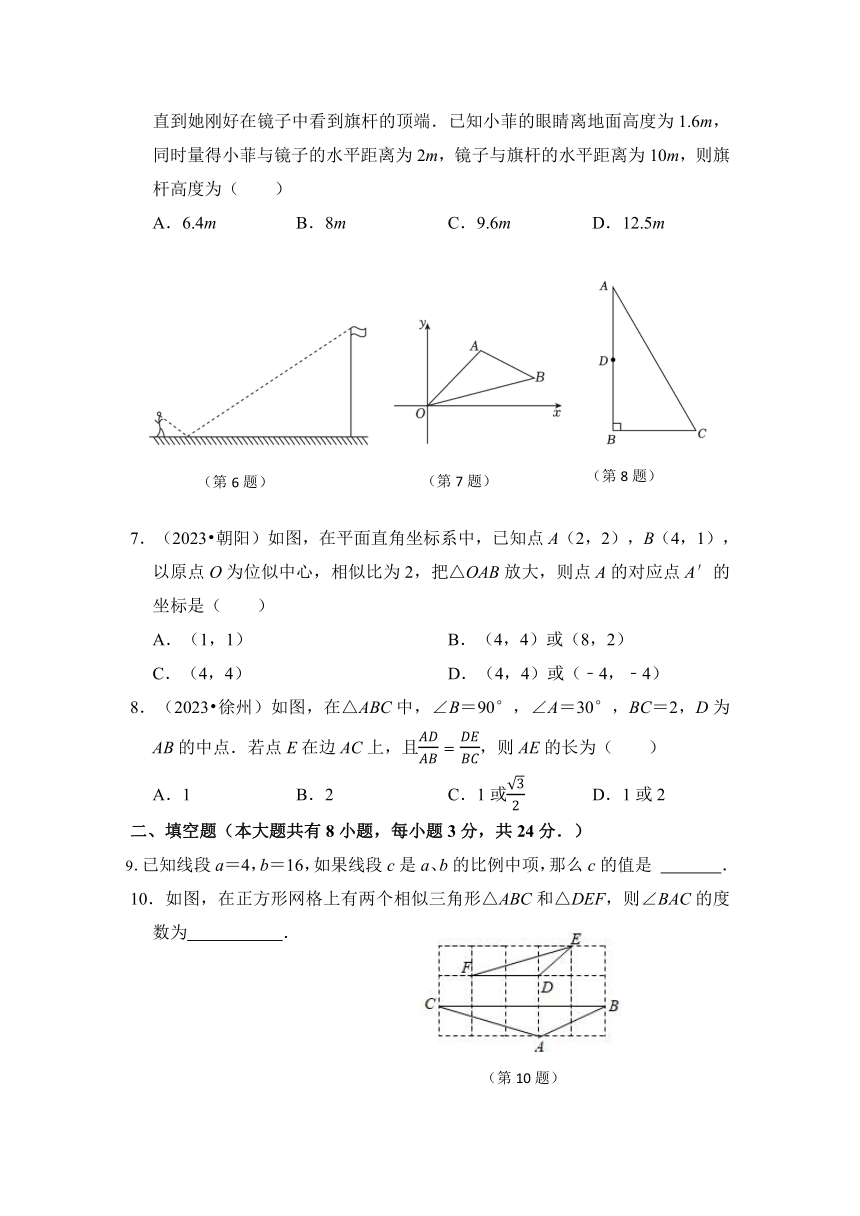
6.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为( )
A.6.4m B.8m C.9.6m D.12.5m
7.(2023 朝阳)如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A′的坐标是( )
A.(1,1) B.(4,4)或(8,2)
C.(4,4) D.(4,4)或(﹣4,﹣4)
8.(2023 徐州)如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边AC上,且,则AE的长为( )
A.1 B.2 C.1或 D.1或2
填空题(本大题共有8小题,每小题3分,共24分.)
9.已知线段a=4,b=16,如果线段c是a、b的比例中项,那么c的值是 .
10.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
11.如图,在△ABC中,点D,E分别在边AB,AC上,添加一个条件使得△ADE∽△ACB,添加的一个条件是 .
12.如图,用一个卡钳(AD=BC,)测量某个零件的内孔直径AB,量得CD长度为6cm,则AB等于 cm.
13.如图,△ABC中,D,E分别是AB,AC的中点,连接DE,则 .
14.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 .
15.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,已知BC=15,AD=10,则这个正方形的面积是 .
16.如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设k,若AD=DF,则 (结果用含k的代数式表示).
三、解答题(本大题共有5小题,共52分.)
17.(本题10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若AB=6,BC=10,求BD的长.
18.(本题10分)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形,.
(1)若AB=8,求线段AD的长.
(2)若△ADE的面积为1,求平行四边形BFED的面积.
19.(本题10分)如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为2:1,并写出点B2的坐标.
20.(本题10分)某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理,来测量东塔的高度.东塔的高度为AB,选取与塔底B在同一水平地面上的E、G两点,分别垂直地面竖立两根高为1.5m的标杆EF和GH,两标杆间隔EG为46m,并且东塔AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2m到D处(即ED=2m),从D处观察A点,A、F、D在一直线上;从标杆GH后退4m到C处(即CG=4m),从C处观察A点,A、H、C三点也在一直线上,且B、E、D、G、C在同一直线上,请你根据以上测量数据,帮助兴趣小组求出东塔AB的高度.
21.(本题12分)【问题呈现】
如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
【类比探究】
如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.
【拓展提升】
如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且.连接BD,CE,求的值;
1-8 AABCDBDD
9. 8 ,10.∠AED=∠B(答案不唯一) , 11.135° ,12.18 ,
13. ,14.(,2)或(,﹣2) , 15. 36 , 16..
17.(1)证明:∵AD是斜边BC上的高,
∴∠BDA=90°,
∵∠BAC=90°,
∴∠BDA=∠BAC,
又∵∠B为公共角,
∴△ABD∽△CBA;
(2)解:由(1)知△ABD∽△CBA,
∴,
∴,
∴BD=3.6.
18.解:(1)∵四边形BFED是平行四边形,
∴DE∥BF,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
∵AB=8,
∴AD=2;
(2)∵△ADE∽△ABC,
∴()2=()2,
∵△ADE的面积为1,
∴△ABC的面积是16,
∵四边形BFED是平行四边形,
∴EF∥AB,
∴△EFC∽△ABC,
∴()2,
∴△EFC的面积=9,
∴平行四边形BFED的面积=16﹣9﹣1=6.
19.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,点B2的坐标为(﹣4,﹣6).
20.解:设BD=x m,则BC=BD+DG+CG=x+46﹣2+4=(x+48)m,
∵AB⊥BC,EF⊥BC,
∴AB∥EF,
∴△ABD∽△FED,
∴,即,
同理可证△ABC∽△HGC,
∴,即,
∴,
解得x=48,
经检验,x=48是原方程的解,
∴,
∴AB=36m,
∴该古建筑AB的高度为36m.
21.证明:∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE;
【类比探究】解:∵△ABC和△ADE都是等腰直角三角形,
∴,∠DAE=∠BAC=45°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴;
【拓展提升】解:(1)∵,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,,
∴∠CAE=∠BAD,
∴△CAE∽△BAD,
∴.
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.若,则ab=( )
A.6 B. C.1 D.
2.(2023 吉林)如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是( )
A. B. C. D.
3.(2023 重庆)若两个相似三角形周长的比为1:4,则这两个三角形对应边的比是( )
A.1:2 B.1:4 C.1:8 D.1:16
4.(2023 东营)如图,△ABC为等边三角形,点D,E分别在边BC,AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
A.1.8 B.2.4 C.3 D.3.2
5.(2023 绵阳)黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形.若CF=4a,则AB=( )
A.(1)a B.(2)a C.(1)a D.(2)a
6.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为( )
A.6.4m B.8m C.9.6m D.12.5m
7.(2023 朝阳)如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A′的坐标是( )
A.(1,1) B.(4,4)或(8,2)
C.(4,4) D.(4,4)或(﹣4,﹣4)
8.(2023 徐州)如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边AC上,且,则AE的长为( )
A.1 B.2 C.1或 D.1或2
填空题(本大题共有8小题,每小题3分,共24分.)
9.已知线段a=4,b=16,如果线段c是a、b的比例中项,那么c的值是 .
10.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
11.如图,在△ABC中,点D,E分别在边AB,AC上,添加一个条件使得△ADE∽△ACB,添加的一个条件是 .
12.如图,用一个卡钳(AD=BC,)测量某个零件的内孔直径AB,量得CD长度为6cm,则AB等于 cm.
13.如图,△ABC中,D,E分别是AB,AC的中点,连接DE,则 .
14.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 .
15.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,已知BC=15,AD=10,则这个正方形的面积是 .
16.如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设k,若AD=DF,则 (结果用含k的代数式表示).
三、解答题(本大题共有5小题,共52分.)
17.(本题10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若AB=6,BC=10,求BD的长.
18.(本题10分)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形,.
(1)若AB=8,求线段AD的长.
(2)若△ADE的面积为1,求平行四边形BFED的面积.
19.(本题10分)如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为2:1,并写出点B2的坐标.
20.(本题10分)某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理,来测量东塔的高度.东塔的高度为AB,选取与塔底B在同一水平地面上的E、G两点,分别垂直地面竖立两根高为1.5m的标杆EF和GH,两标杆间隔EG为46m,并且东塔AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2m到D处(即ED=2m),从D处观察A点,A、F、D在一直线上;从标杆GH后退4m到C处(即CG=4m),从C处观察A点,A、H、C三点也在一直线上,且B、E、D、G、C在同一直线上,请你根据以上测量数据,帮助兴趣小组求出东塔AB的高度.
21.(本题12分)【问题呈现】
如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
【类比探究】
如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.
【拓展提升】
如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且.连接BD,CE,求的值;
1-8 AABCDBDD
9. 8 ,10.∠AED=∠B(答案不唯一) , 11.135° ,12.18 ,
13. ,14.(,2)或(,﹣2) , 15. 36 , 16..
17.(1)证明:∵AD是斜边BC上的高,
∴∠BDA=90°,
∵∠BAC=90°,
∴∠BDA=∠BAC,
又∵∠B为公共角,
∴△ABD∽△CBA;
(2)解:由(1)知△ABD∽△CBA,
∴,
∴,
∴BD=3.6.
18.解:(1)∵四边形BFED是平行四边形,
∴DE∥BF,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
∵AB=8,
∴AD=2;
(2)∵△ADE∽△ABC,
∴()2=()2,
∵△ADE的面积为1,
∴△ABC的面积是16,
∵四边形BFED是平行四边形,
∴EF∥AB,
∴△EFC∽△ABC,
∴()2,
∴△EFC的面积=9,
∴平行四边形BFED的面积=16﹣9﹣1=6.
19.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,点B2的坐标为(﹣4,﹣6).
20.解:设BD=x m,则BC=BD+DG+CG=x+46﹣2+4=(x+48)m,
∵AB⊥BC,EF⊥BC,
∴AB∥EF,
∴△ABD∽△FED,
∴,即,
同理可证△ABC∽△HGC,
∴,即,
∴,
解得x=48,
经检验,x=48是原方程的解,
∴,
∴AB=36m,
∴该古建筑AB的高度为36m.
21.证明:∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE;
【类比探究】解:∵△ABC和△ADE都是等腰直角三角形,
∴,∠DAE=∠BAC=45°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴;
【拓展提升】解:(1)∵,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,,
∴∠CAE=∠BAD,
∴△CAE∽△BAD,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
