4.1平方根(2)课件(共18张PPT) 苏科版八年级数学上册
文档属性
| 名称 | 4.1平方根(2)课件(共18张PPT) 苏科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 422.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
八年级(上册)
初中数学
4.1 平方根(2)
1.说出下列各数的平方根.
25, 0, , 21, -64.
2.一个数的平方等于它本身,这个数是______;
一个数的平方根等于它本身,这个数是______;
3.若3a+1有平方根,那么a的取值范围_______;
4.若4a+1的平方根是±5,则a=________;
复习回顾
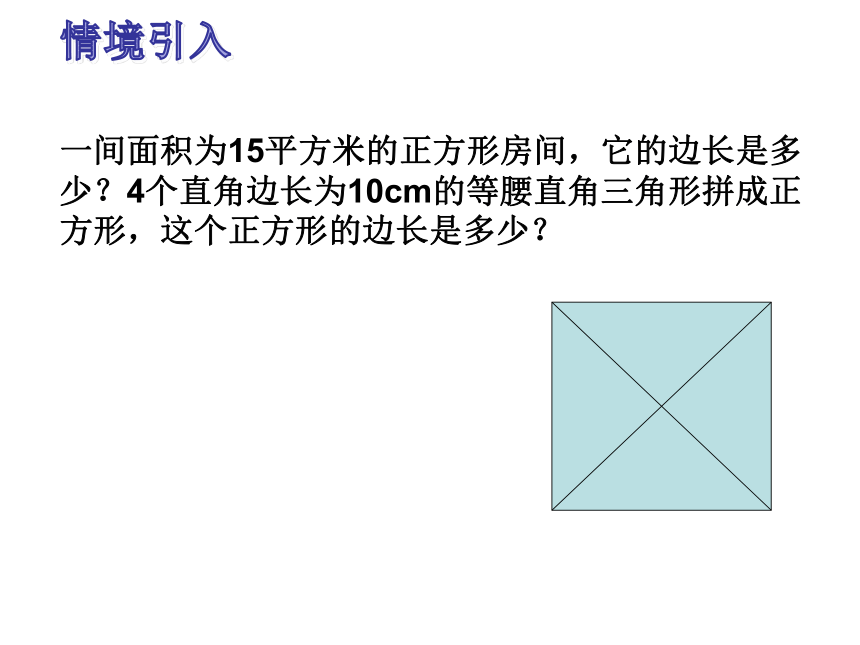
一间面积为15平方米的正方形房间,它的边长是多少?4个直角边长为10cm的等腰直角三角形拼成正方形,这个正方形的边长是多少?
情境引入
正数a有两个平方根± ,其中正数a的正的平方根 ,叫做a的算术平方根.
如:(1)4的平方根是______, 其中____是4的算术平方根,记作__________;
(2)7的平方根是______, 其中____是7的算术平方根;
(3)0算术平方根是_____,记作_________;
(4) 读作_______,表示________________,结果是______.
新课讲授
±2
2
根号9
0
9的算术平方根
3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
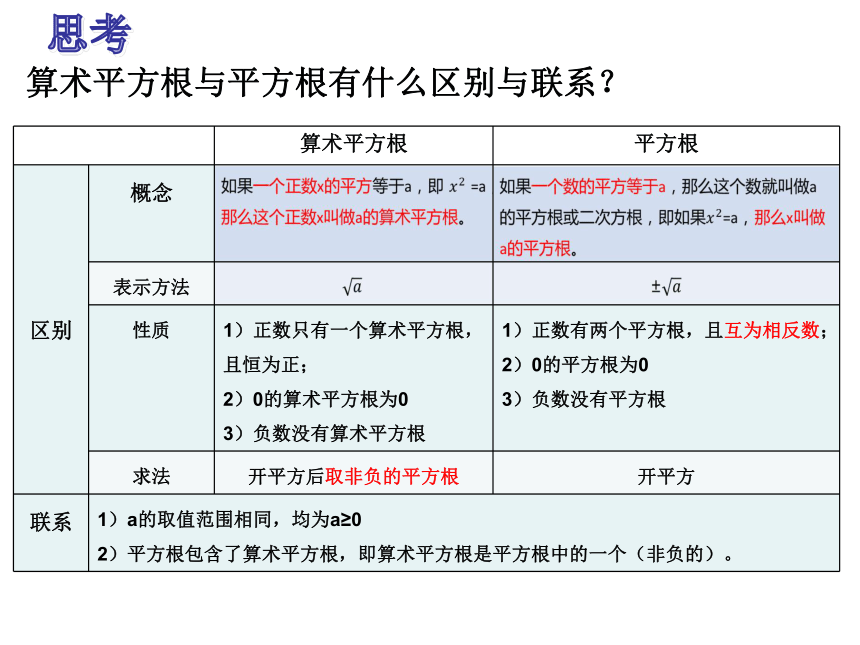
算术平方根
平方根
区别
概念
表示方法
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
思考
算术平方根与平方根有什么区别与联系?
例1 求下列各数的算术平方根:
(1)625;(2)0.0081;(3)7;(4)0.
例题讲解
一个数的算术平方根等于它本身,这个数是_______。
( )2、( )2 、
有意义吗?如果有,求它的值.
例题讲解
例2
(1)( )2= (2) =
(3)( )2= (4) =
(5)( )2= (6) =
(7)( )2= (8) =
例3 完成下列习题,做题后思考讨论交流.
例题讲解
a
│a│
(a≥0)
想一想:
两个式子分别表示什么意义?有什么区别?
总结归纳
( )2=a( a ≥0)
a2=|a|=
a(a≥0)
-a(a<0)
例4 “欲穷千里目,更上一层楼”说的是登得高看得远.如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 ,其中R是地球半径,约等于6400km.
小丽站在海边一块岩石上,眼睛离地面的高度h为20m,她观测到远处一艘船刚露出海平面,求此时d的值.
例题讲解
(1) =________.
(2) 的算术平方根是________.
(3) 的平方根是________.
课堂练习
1.填空
2.若x<2,则 _________
3. = __________
课堂练习
课堂练习
4.式子
有意义,则x的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≤3
5.若a是(﹣4)2的平方根,b的一个平方根是2,则代数式a+b的值为( )A.8 B.0 C.8或0 D.4或﹣4
课堂练习
6.下列语句正确的是( )A.10的平方根是100
B.100的平方根是10C.-2是-4的平方根
D. 的平方根是±
49
?
23
?
课堂练习
7.一个数的算术平方根为2m-6,它的平方根为±(m-1),求m的值.
1.若 ,则 的平方根是_____;
2.已知△ABC的三边分别是a、b、c,且 ,则c的取值范围为_________
拓展提高
3.已知y= + +3,求xy的算术平方根。
4.在△ABC中,∠C=90°.
(1)如果AC=5,BC=12,求AB;
(2)如果AC=2,BC=1,求AB;
(3)如果AB=25,BC=24,求AC;
(4)如果AC=5,AB=12,求BC;
拓展提高
1.你能说出一些数的平方根与算术平方根吗?
2.算术平方根与平方根有什么区别与联系?
课堂小结
八年级(上册)
初中数学
4.1 平方根(2)
1.说出下列各数的平方根.
25, 0, , 21, -64.
2.一个数的平方等于它本身,这个数是______;
一个数的平方根等于它本身,这个数是______;
3.若3a+1有平方根,那么a的取值范围_______;
4.若4a+1的平方根是±5,则a=________;
复习回顾
一间面积为15平方米的正方形房间,它的边长是多少?4个直角边长为10cm的等腰直角三角形拼成正方形,这个正方形的边长是多少?
情境引入
正数a有两个平方根± ,其中正数a的正的平方根 ,叫做a的算术平方根.
如:(1)4的平方根是______, 其中____是4的算术平方根,记作__________;
(2)7的平方根是______, 其中____是7的算术平方根;
(3)0算术平方根是_____,记作_________;
(4) 读作_______,表示________________,结果是______.
新课讲授
±2
2
根号9
0
9的算术平方根
3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
算术平方根
平方根
区别
概念
表示方法
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
思考
算术平方根与平方根有什么区别与联系?
例1 求下列各数的算术平方根:
(1)625;(2)0.0081;(3)7;(4)0.
例题讲解
一个数的算术平方根等于它本身,这个数是_______。
( )2、( )2 、
有意义吗?如果有,求它的值.
例题讲解
例2
(1)( )2= (2) =
(3)( )2= (4) =
(5)( )2= (6) =
(7)( )2= (8) =
例3 完成下列习题,做题后思考讨论交流.
例题讲解
a
│a│
(a≥0)
想一想:
两个式子分别表示什么意义?有什么区别?
总结归纳
( )2=a( a ≥0)
a2=|a|=
a(a≥0)
-a(a<0)
例4 “欲穷千里目,更上一层楼”说的是登得高看得远.如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 ,其中R是地球半径,约等于6400km.
小丽站在海边一块岩石上,眼睛离地面的高度h为20m,她观测到远处一艘船刚露出海平面,求此时d的值.
例题讲解
(1) =________.
(2) 的算术平方根是________.
(3) 的平方根是________.
课堂练习
1.填空
2.若x<2,则 _________
3. = __________
课堂练习
课堂练习
4.式子
有意义,则x的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≤3
5.若a是(﹣4)2的平方根,b的一个平方根是2,则代数式a+b的值为( )A.8 B.0 C.8或0 D.4或﹣4
课堂练习
6.下列语句正确的是( )A.10的平方根是100
B.100的平方根是10C.-2是-4的平方根
D. 的平方根是±
49
?
23
?
课堂练习
7.一个数的算术平方根为2m-6,它的平方根为±(m-1),求m的值.
1.若 ,则 的平方根是_____;
2.已知△ABC的三边分别是a、b、c,且 ,则c的取值范围为_________
拓展提高
3.已知y= + +3,求xy的算术平方根。
4.在△ABC中,∠C=90°.
(1)如果AC=5,BC=12,求AB;
(2)如果AC=2,BC=1,求AB;
(3)如果AB=25,BC=24,求AC;
(4)如果AC=5,AB=12,求BC;
拓展提高
1.你能说出一些数的平方根与算术平方根吗?
2.算术平方根与平方根有什么区别与联系?
课堂小结
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
