第1章勾股定理的证明及应用课件(共25张PPT)2023--2024学年北师大版八年级数学上册
文档属性
| 名称 | 第1章勾股定理的证明及应用课件(共25张PPT)2023--2024学年北师大版八年级数学上册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 466.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
美丽的勾股树
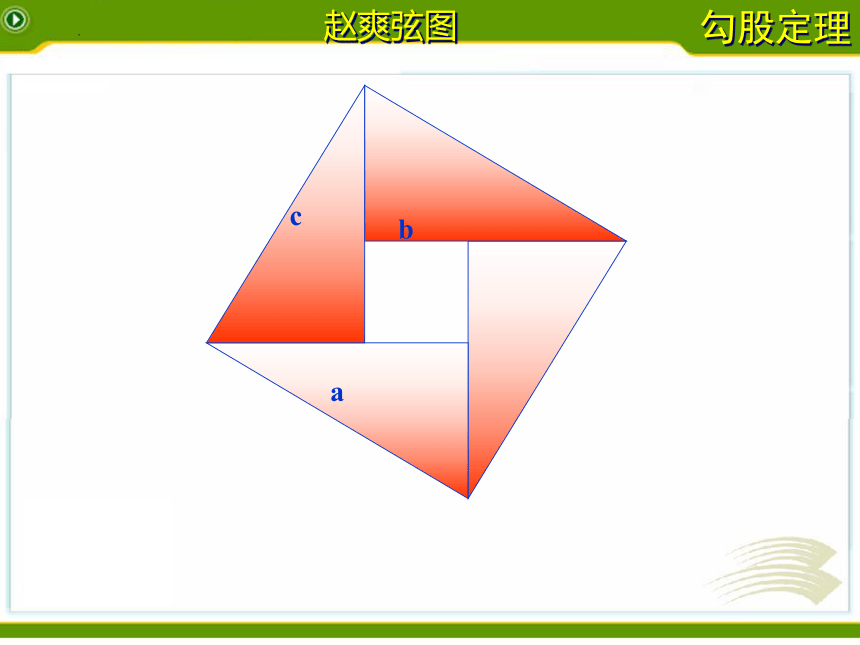
拼图游戏
a
b
c
赵爽弦图
a
印度婆什迦罗的证明
c
c2 = b2 + a2
b
a2 + b2 = c2
a2
b2
a2
c2
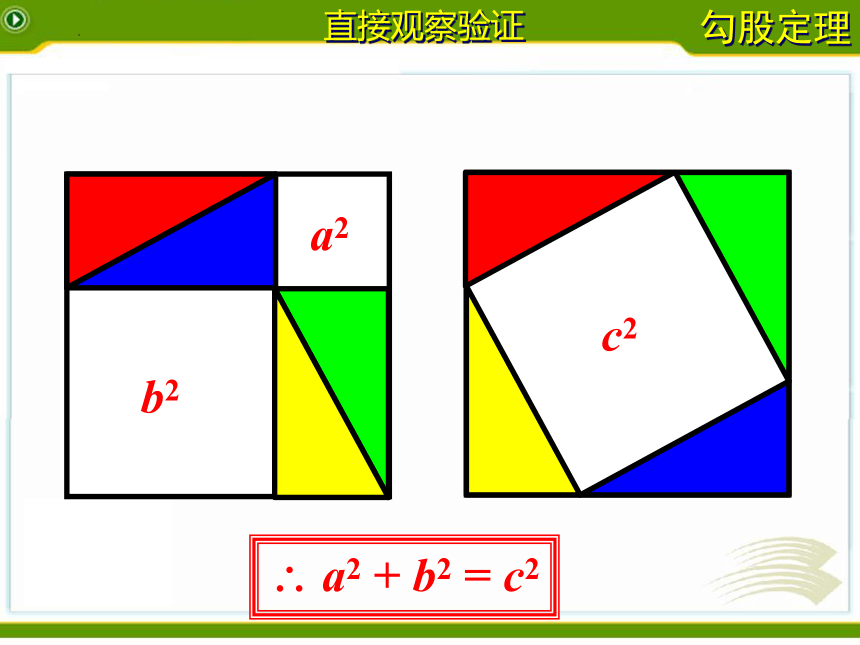
直接观察验证
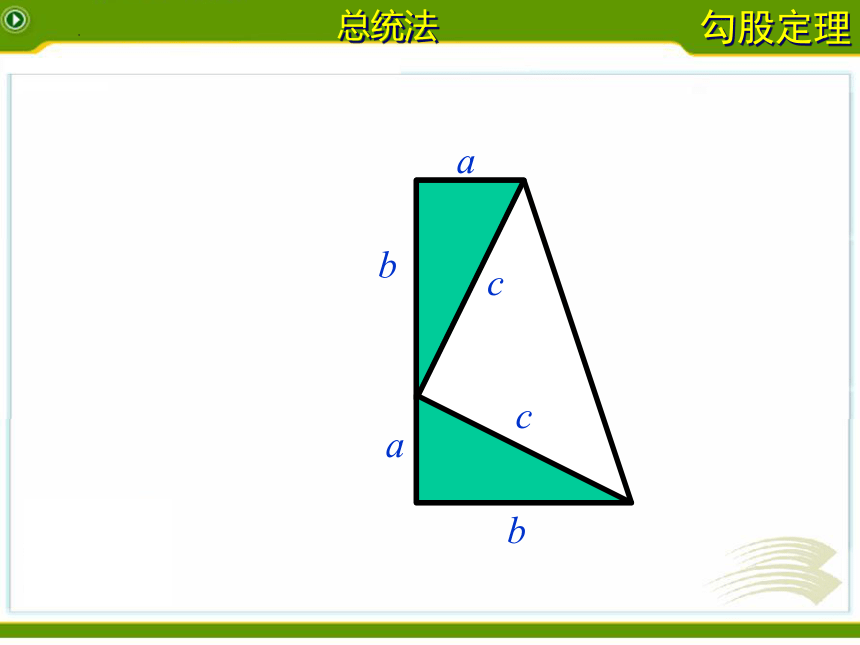
总统法
a
a
b
b
c
c
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
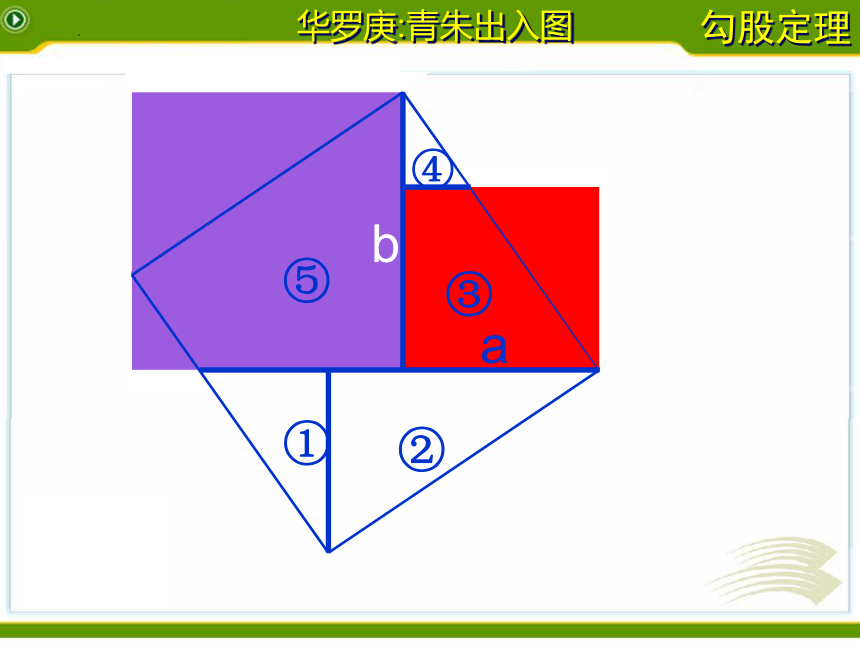
华罗庚:青朱出入图
a
b
c
①
②
③
④
⑤
华罗庚:青朱出入图
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
勾股定理逆定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形
作用:计算长度与判断是否是直角三角形
概念复习
1
1
5
12
13
7
24
25
9
40
41
1
2
3
4
5
常见的直角三角形
3 ,4 ,5
5, 12 ,13
7, 24 ,25
9 ,40 ,41
11, 60 ,61
13, 84, 85
15, 112 ,113
8,15,17
9, 12, 15
12,35,37
20,21,29
20,99,101
48,55,73
60,91,109
常见勾股数
比一比看看谁算得快!
求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
基本方法
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
基本方法
3.已知一个Rt△的两边长分别为3和4,
则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5
④若a∶b=3∶4,c=10,
则Rt△ABC的面积为________。
②若a=15,c=25,则b=___________;
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
③若c=61,b=60,则a=__________;
13
20
11
24
A
D
基础练习
1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形; B.直角三角形;
C.等腰三角形或直角三角形; D.等腰直角三角形。
2.若△ABC的三边a、b、c,满足a:b:c=1:1: ,试判断△ABC的形状
基础练习
郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解三角形:设未知数求长度
印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”,
请用学过的数学知识回答这个问题。
2
X+0.5
X
C
B
A
荷花问题
如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
折叠问题
等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
A
B
C
D
13
13
10
H
面积法求三角形的高
如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
A
B
C
D
30°
8
求三角形的边长
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
平面展开问题
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
平面展开问题
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
A
B
我怎么走
会最近呢
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
平面展开问题
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
152
美丽的勾股树
拼图游戏
a
b
c
赵爽弦图
a
印度婆什迦罗的证明
c
c2 = b2 + a2
b
a2 + b2 = c2
a2
b2
a2
c2
直接观察验证
总统法
a
a
b
b
c
c
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
华罗庚:青朱出入图
a
b
c
①
②
③
④
⑤
华罗庚:青朱出入图
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
勾股定理逆定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形
作用:计算长度与判断是否是直角三角形
概念复习
1
1
5
12
13
7
24
25
9
40
41
1
2
3
4
5
常见的直角三角形
3 ,4 ,5
5, 12 ,13
7, 24 ,25
9 ,40 ,41
11, 60 ,61
13, 84, 85
15, 112 ,113
8,15,17
9, 12, 15
12,35,37
20,21,29
20,99,101
48,55,73
60,91,109
常见勾股数
比一比看看谁算得快!
求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
基本方法
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
基本方法
3.已知一个Rt△的两边长分别为3和4,
则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5
④若a∶b=3∶4,c=10,
则Rt△ABC的面积为________。
②若a=15,c=25,则b=___________;
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
③若c=61,b=60,则a=__________;
13
20
11
24
A
D
基础练习
1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形; B.直角三角形;
C.等腰三角形或直角三角形; D.等腰直角三角形。
2.若△ABC的三边a、b、c,满足a:b:c=1:1: ,试判断△ABC的形状
基础练习
郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解三角形:设未知数求长度
印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”,
请用学过的数学知识回答这个问题。
2
X+0.5
X
C
B
A
荷花问题
如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
折叠问题
等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
A
B
C
D
13
13
10
H
面积法求三角形的高
如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
A
B
C
D
30°
8
求三角形的边长
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
平面展开问题
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
平面展开问题
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
A
B
我怎么走
会最近呢
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
平面展开问题
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
152
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
