1.2.3相反数课件(共23张PPT)2023—2024学年人教版数学七年级上册
文档属性
| 名称 | 1.2.3相反数课件(共23张PPT)2023—2024学年人教版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 505.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 15:11:45 | ||
图片预览





文档简介
(共23张PPT)
课前问题(0.5分钟)
1、什么是数轴?
2、数轴的三要素是什么
答:1.数轴是规定了原点、正方向、单位长度的一条直线。
2.原点、正方向、单位长度
观察数轴标上的数有特点?
0
1
2
3
-1
-2
-3
4
5
学习目标 (0.5分钟)
1.借助于数轴,理解相反数的概念。
2.掌握相反数的意义,会求一个数的相反数。
1.2 有理数(第3课时)
1.2.3 相反数
导入新课
情境引入
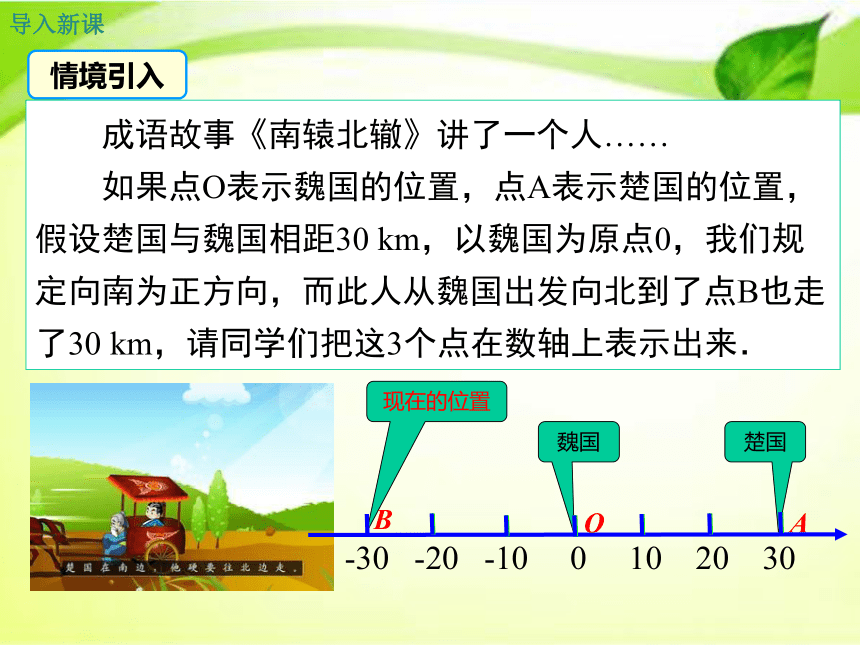
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,假设楚国与魏国相距30 km,以魏国为原点0,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
B
A
-30 -20 -10 0 10 20 30
讲授新课
相反数
一
合作探究
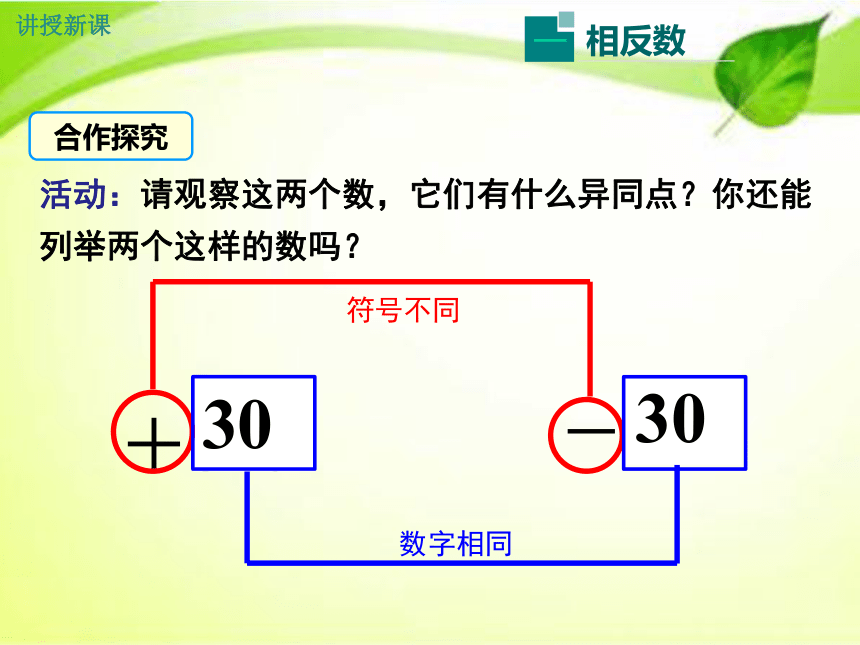
活动:请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
30
30
数字相同
符号不同
+
-
数字相同
符号不同
+
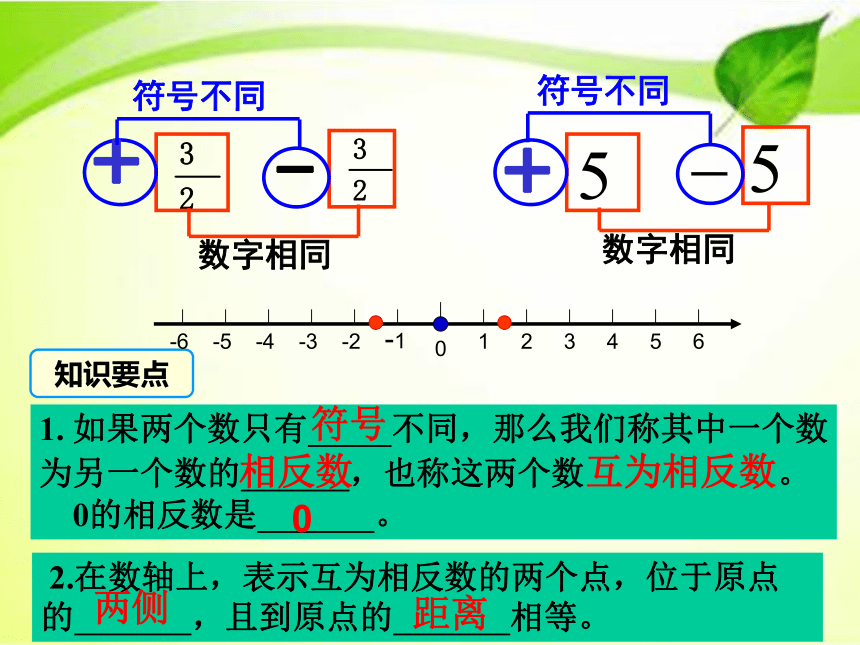
知识要点
1. 如果两个数只有 不同,那么我们称其中一个数
为另一个数的 ,也称这两个数互为相反数。
0的相反数是 。
符号
相反数
0
2.在数轴上,表示互为相反数的两个点,位于原点的 ,且到原点的 相等。
两侧
距离
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
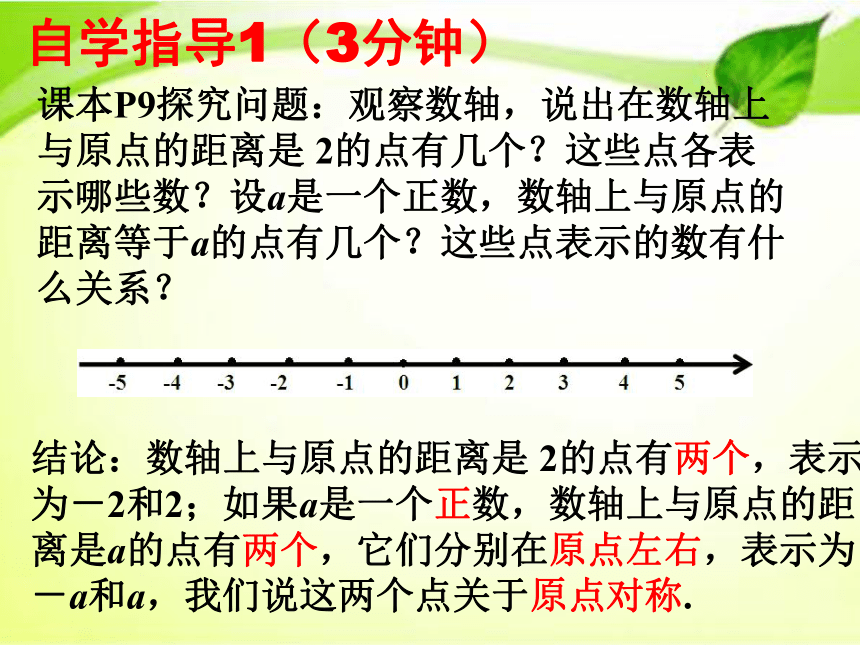
课本P9探究问题:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
结论:数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
自学指导1(3分钟)
请回答: 如果两个数只有 不同,那么我们称其中一个数为另一个的 ,也称这两个数互为相反数。0的相反数是 。
符号
相反数
0
例.(2018 长沙模拟)下列各组数中,互为相反数的是( )
A.-2 与2 B.2与2 C.3与1/3 D.3与3
A
变式1.如果a与 互为相反数,则a等于 .
-
变式2.如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是 .
点D
结论:在数轴上,互为相反数的两个数所表示的点分居在原点的两侧,且到原点的距离相等.
判断题:
(1)-5是5的相反数( );
(2)-5是相反数( );
(3) 与 互为相反数( );
(4)-5和5互为相反数( );
(5) 相反数等于它本身的数只有0 ﹙ ﹚;
(6) 符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
自学检测1(4分钟)
小游戏:一个学生说出一个数,然后指定另一名学生回答它的相反数,两人再交换出题,比一比,看哪组回答的又快又准.
思考:a的相反数是什么?
a 的相反数是-a , a可表示任意有理数.
求任意一个数的相反数,就可以在这个数前加一个“-”号.
自学指导2(3分钟)多重符号的化简
-(+1.1)表示什么?-(-7)呢?
-(-9.8)呢?它们的结果应是多少?
问题:若把 a分别换成+5,-7,0时,这些数的相反数怎样表示?
a = +5, - a = -(+5)
a = -7, - a = -(-7)
a = 0, - a = 0
例1
(1) 是____的相反数,
(2) 是______的相反数, =______ .
(3) 是_______的相反数, .
(4) 是_______的相反数, .
+4
-4
典例精析
问题:在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
在一个数前面加上“+”仍表示这个数,“+”号可省略.
问题:如何进行符号化简呢?你能自己总结出简化符号的规律吗?
例3:化简:
(1) -(+1)=_________; (2)-(-2)=_________; (3)+(+3)=_________; (4)+(-4)=_________; (5)-[+(-5)]=______.
-1
2
3
-4
5
总结:1、在任意一个数前面填上“+”号,表示这个数 _______;
在任意一个数前面填 上“-”号表示这个数的_______.
本身
相反数
练习3:化简:
(1) +(+1)=________; (2)+(-2)=________;(3)+(-3)=________;
(4) -(+4)=________; (5)-[-(-5)]=________.
1
-2
-3
-4
-5
2、括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.
由内向外依次去括号
1.求下列各数的相反数。
(1)5 (2)-0.2 (3)0
(4)a (5)-(-2)
解:(1)5的相反数是-5;
(2)-0.2的相反数是0.2
(3)0的相反数是0
(4)a的相反数是-a;
(5) -(-2)的相反数是-2.
任何数的相反数就是在这个数的前面添上一个负号
自学检测2(4分钟)
2、化简下列各数
(1)-(+10) (2)+(-0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
解:
(1)-(+10)=-10
(2)+(-0.15)=-0.15
(3)+(+3)=3
(4)-(-12)=12
(5)+[-(-1.1)]=+(+1.1)=1.1
(6)-[+(-7)]=-(-7)=7
由内向外依次去括号
1.-1.6是____的相反数,____的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与
C. 与
3.5的相反数是____;a的相反数是___;
1.6
-a
-5
C
-0.3
当堂训练
变式1. 如果a与-2互为相反数,那么a等于( )
A.-2 B.2 C.- D.
4. -2的相反数是( )
A.-2 B.- C.2 D.
变式2. 如图,数轴上的点A表示的数为a,则a的相反数等于( )
A.-2 B.2 C. D.
C
B
B
变式3. 如图,数轴上的单位长度为1,有三个点A、B、C,若点A、B表示的数互为相反数,则图中点C对应的数是( )
A.-2 B.0 C.1 D.4
C
5.若a=-13,则-a=____;若-a=-6,则a=___ .
6.若a是负数,则-a是_____数;若-a是负数,则
a是_____数.
7. 的相反数是_____,-3x的相反数是___.
13
6
正
3x
正
8、化简下列各数:
(1)-(+0.75)=____ __; (2)-(-68)=______;
(3)+(-0.5)=______; (4)+(+3.8)=______.
9、已知2n-3与-9互为相反数,求n的值.
-0.75
68
-0.5
3.8
解:∵-9的相反数是9
∴2n-3 = 9
∴n = 6
课堂小结
1.相反数的概念:只有符号不同的两个数叫做互为相反数;特别地,0的相反数是0.
2. 表示求 的相反数.
课前问题(0.5分钟)
1、什么是数轴?
2、数轴的三要素是什么
答:1.数轴是规定了原点、正方向、单位长度的一条直线。
2.原点、正方向、单位长度
观察数轴标上的数有特点?
0
1
2
3
-1
-2
-3
4
5
学习目标 (0.5分钟)
1.借助于数轴,理解相反数的概念。
2.掌握相反数的意义,会求一个数的相反数。
1.2 有理数(第3课时)
1.2.3 相反数
导入新课
情境引入
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,假设楚国与魏国相距30 km,以魏国为原点0,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
B
A
-30 -20 -10 0 10 20 30
讲授新课
相反数
一
合作探究
活动:请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
30
30
数字相同
符号不同
+
-
数字相同
符号不同
+
知识要点
1. 如果两个数只有 不同,那么我们称其中一个数
为另一个数的 ,也称这两个数互为相反数。
0的相反数是 。
符号
相反数
0
2.在数轴上,表示互为相反数的两个点,位于原点的 ,且到原点的 相等。
两侧
距离
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
课本P9探究问题:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
结论:数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
自学指导1(3分钟)
请回答: 如果两个数只有 不同,那么我们称其中一个数为另一个的 ,也称这两个数互为相反数。0的相反数是 。
符号
相反数
0
例.(2018 长沙模拟)下列各组数中,互为相反数的是( )
A.-2 与2 B.2与2 C.3与1/3 D.3与3
A
变式1.如果a与 互为相反数,则a等于 .
-
变式2.如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是 .
点D
结论:在数轴上,互为相反数的两个数所表示的点分居在原点的两侧,且到原点的距离相等.
判断题:
(1)-5是5的相反数( );
(2)-5是相反数( );
(3) 与 互为相反数( );
(4)-5和5互为相反数( );
(5) 相反数等于它本身的数只有0 ﹙ ﹚;
(6) 符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
自学检测1(4分钟)
小游戏:一个学生说出一个数,然后指定另一名学生回答它的相反数,两人再交换出题,比一比,看哪组回答的又快又准.
思考:a的相反数是什么?
a 的相反数是-a , a可表示任意有理数.
求任意一个数的相反数,就可以在这个数前加一个“-”号.
自学指导2(3分钟)多重符号的化简
-(+1.1)表示什么?-(-7)呢?
-(-9.8)呢?它们的结果应是多少?
问题:若把 a分别换成+5,-7,0时,这些数的相反数怎样表示?
a = +5, - a = -(+5)
a = -7, - a = -(-7)
a = 0, - a = 0
例1
(1) 是____的相反数,
(2) 是______的相反数, =______ .
(3) 是_______的相反数, .
(4) 是_______的相反数, .
+4
-4
典例精析
问题:在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
在一个数前面加上“+”仍表示这个数,“+”号可省略.
问题:如何进行符号化简呢?你能自己总结出简化符号的规律吗?
例3:化简:
(1) -(+1)=_________; (2)-(-2)=_________; (3)+(+3)=_________; (4)+(-4)=_________; (5)-[+(-5)]=______.
-1
2
3
-4
5
总结:1、在任意一个数前面填上“+”号,表示这个数 _______;
在任意一个数前面填 上“-”号表示这个数的_______.
本身
相反数
练习3:化简:
(1) +(+1)=________; (2)+(-2)=________;(3)+(-3)=________;
(4) -(+4)=________; (5)-[-(-5)]=________.
1
-2
-3
-4
-5
2、括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.
由内向外依次去括号
1.求下列各数的相反数。
(1)5 (2)-0.2 (3)0
(4)a (5)-(-2)
解:(1)5的相反数是-5;
(2)-0.2的相反数是0.2
(3)0的相反数是0
(4)a的相反数是-a;
(5) -(-2)的相反数是-2.
任何数的相反数就是在这个数的前面添上一个负号
自学检测2(4分钟)
2、化简下列各数
(1)-(+10) (2)+(-0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
解:
(1)-(+10)=-10
(2)+(-0.15)=-0.15
(3)+(+3)=3
(4)-(-12)=12
(5)+[-(-1.1)]=+(+1.1)=1.1
(6)-[+(-7)]=-(-7)=7
由内向外依次去括号
1.-1.6是____的相反数,____的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与
C. 与
3.5的相反数是____;a的相反数是___;
1.6
-a
-5
C
-0.3
当堂训练
变式1. 如果a与-2互为相反数,那么a等于( )
A.-2 B.2 C.- D.
4. -2的相反数是( )
A.-2 B.- C.2 D.
变式2. 如图,数轴上的点A表示的数为a,则a的相反数等于( )
A.-2 B.2 C. D.
C
B
B
变式3. 如图,数轴上的单位长度为1,有三个点A、B、C,若点A、B表示的数互为相反数,则图中点C对应的数是( )
A.-2 B.0 C.1 D.4
C
5.若a=-13,则-a=____;若-a=-6,则a=___ .
6.若a是负数,则-a是_____数;若-a是负数,则
a是_____数.
7. 的相反数是_____,-3x的相反数是___.
13
6
正
3x
正
8、化简下列各数:
(1)-(+0.75)=____ __; (2)-(-68)=______;
(3)+(-0.5)=______; (4)+(+3.8)=______.
9、已知2n-3与-9互为相反数,求n的值.
-0.75
68
-0.5
3.8
解:∵-9的相反数是9
∴2n-3 = 9
∴n = 6
课堂小结
1.相反数的概念:只有符号不同的两个数叫做互为相反数;特别地,0的相反数是0.
2. 表示求 的相反数.
