2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题(含解析)
文档属性
| 名称 | 2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 18:52:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题
一、选择题(本大题共6小题,每小题2分,共12分.)
1. 二次函数y=3(x+1)2-2的图像的顶点坐标是( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
2. 已知一元二次方程x2-8x+c=0有一个根为2,则另一个根为( )
A.10 B.6 C.8 D.-2
某校开展创建“书香校园”的活动,活动期间对某班位学生所阅读书籍数量的情况进行了统计,
并得到如下所示的统计表,则这组数据的中位数和众数分别是( )
阅读书籍数量 本 本 本 本以上
人数(单位:人)
A., B., C., D.,
4 . 抛物线y=x2向左平移1个单位,再向上平移2个单位后,
所得抛物线的表达式是( )
A.y=(x+1)2﹣2 B.y=(x﹣1)2+2
C.y=(x﹣1)2﹣2 D.y=(x+1)2+2
5 .如图,A,B,C,D为上的点,且直线与夹角为.
若,,的长分别为,和,则的半径是( )
A. 4 B. C. 5 D.
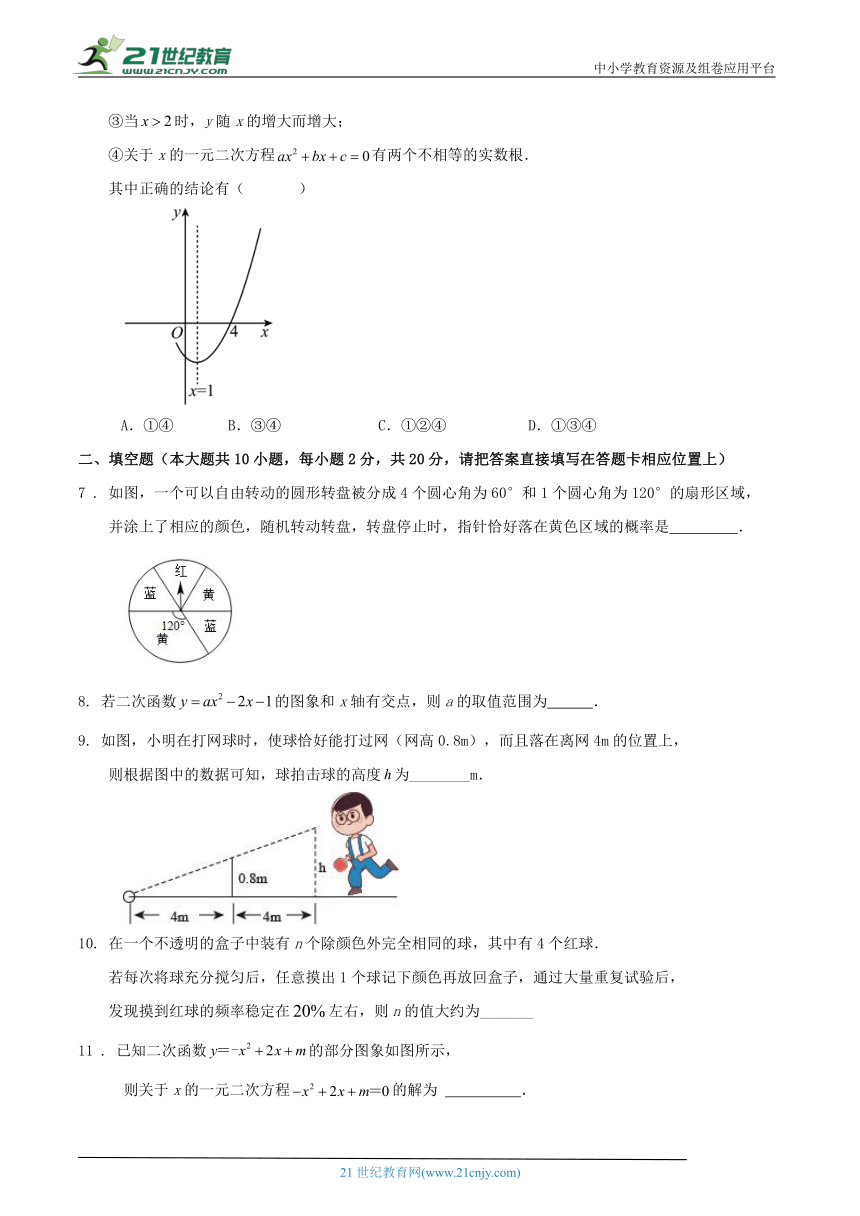
6 . 如图,抛物线与x轴交于点(4,0),其对称轴为直线,
结合图像,下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有两个不相等的实数根.
其中正确的结论有( )
A.①④ B.③④ C.①②④ D.①③④
二、填空题(本大题共10小题,每小题2分,共20分,请把答案直接填写在答题卡相应位置上)
7 . 如图,一个可以自由转动的圆形转盘被分成4个圆心角为60°和1个圆心角为120°的扇形区域,
并涂上了相应的颜色,随机转动转盘,转盘停止时,指针恰好落在黄色区域的概率是 .
8. 若二次函数的图象和x轴有交点,则a的取值范围为 .
如图,小明在打网球时,使球恰好能打过网(网高0.8m),而且落在离网4m的位置上,
则根据图中的数据可知,球拍击球的高度为________m.
在一个不透明的盒子中装有n个除颜色外完全相同的球,其中有4个红球.
若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,
发现摸到红球的频率稳定在左右,则n的值大约为_______
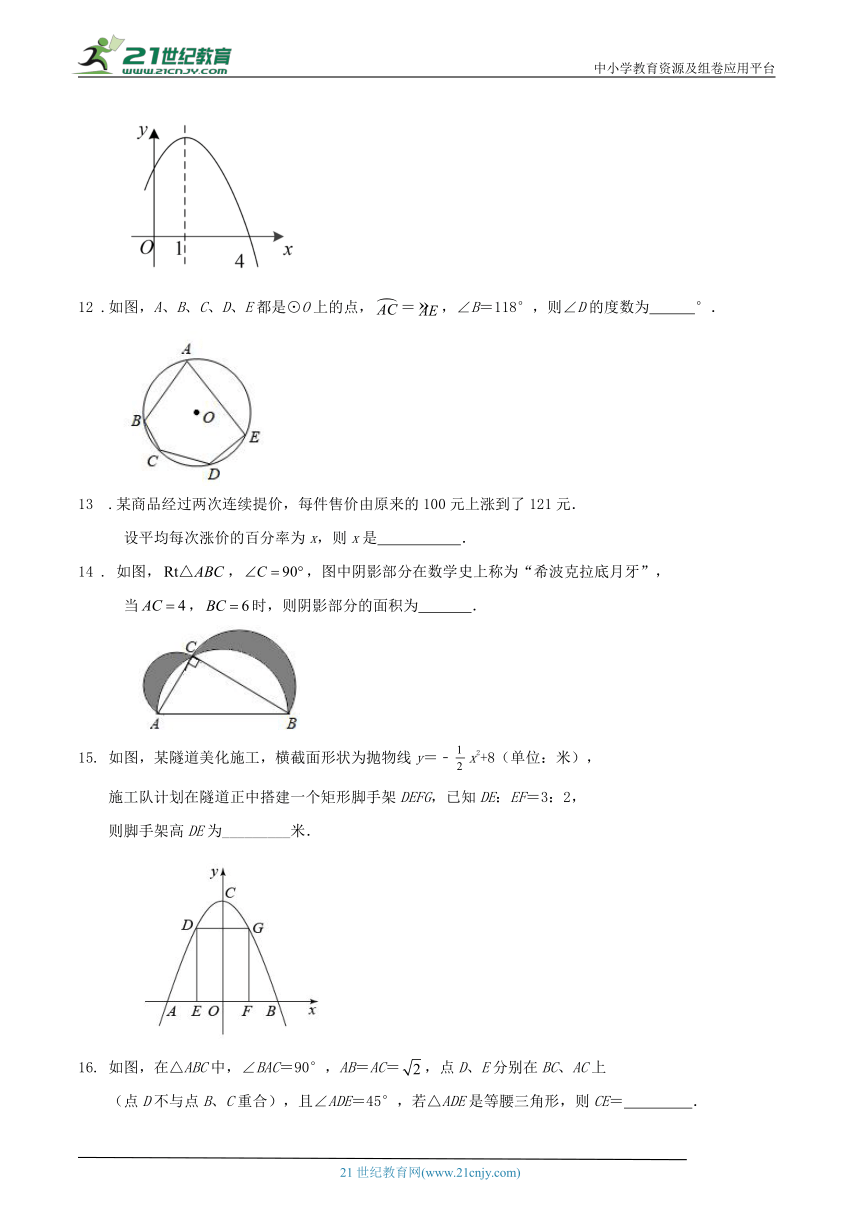
11 . 已知二次函数的部分图象如图所示,
则关于x的一元二次方程的解为 .
12 .如图,A、B、C、D、E都是⊙O上的点,=,∠B=118°,则∠D的度数为 °.
13 .某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
14 . 如图,,,图中阴影部分在数学史上称为“希波克拉底月牙”,
当,时,则阴影部分的面积为 .
如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),
施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,
则脚手架高DE为_________米.
如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上
(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
三、解答题(本大题共11小题,共88分.解答时应写出文字说明、证明过程或演算步骤)
17. 解方程:
(1).
(2).
18 .劳动教育已纳入人才培养全过程,某学校加大投入,建设校园农场,
该农场一种作物的产量两年内从300千克增加到363千克.若平均每年的增产率相同,
求平均每年的增产率.
为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.
竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)小云抽中B组试题的概率是 ;
(2)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
王老师为了选拔一名学生参加数学比赛,
对两名备赛选手进行了10次测验,成绩如下(单位:分):
甲:5,6,6,6,6,6,7,9,9,10
乙:5,6,6,6,7,7,7,7,9,10
选手 平均数 中位数 众数 方差
甲 7 a 6
乙 b 7 c d
(1)以上成绩统计分析表中_______,________,______;
(2)d______(填“>”、<或“=”):
(3)根据以上信息,你认为王老师应该选哪位同学参加比赛,请说明理由.
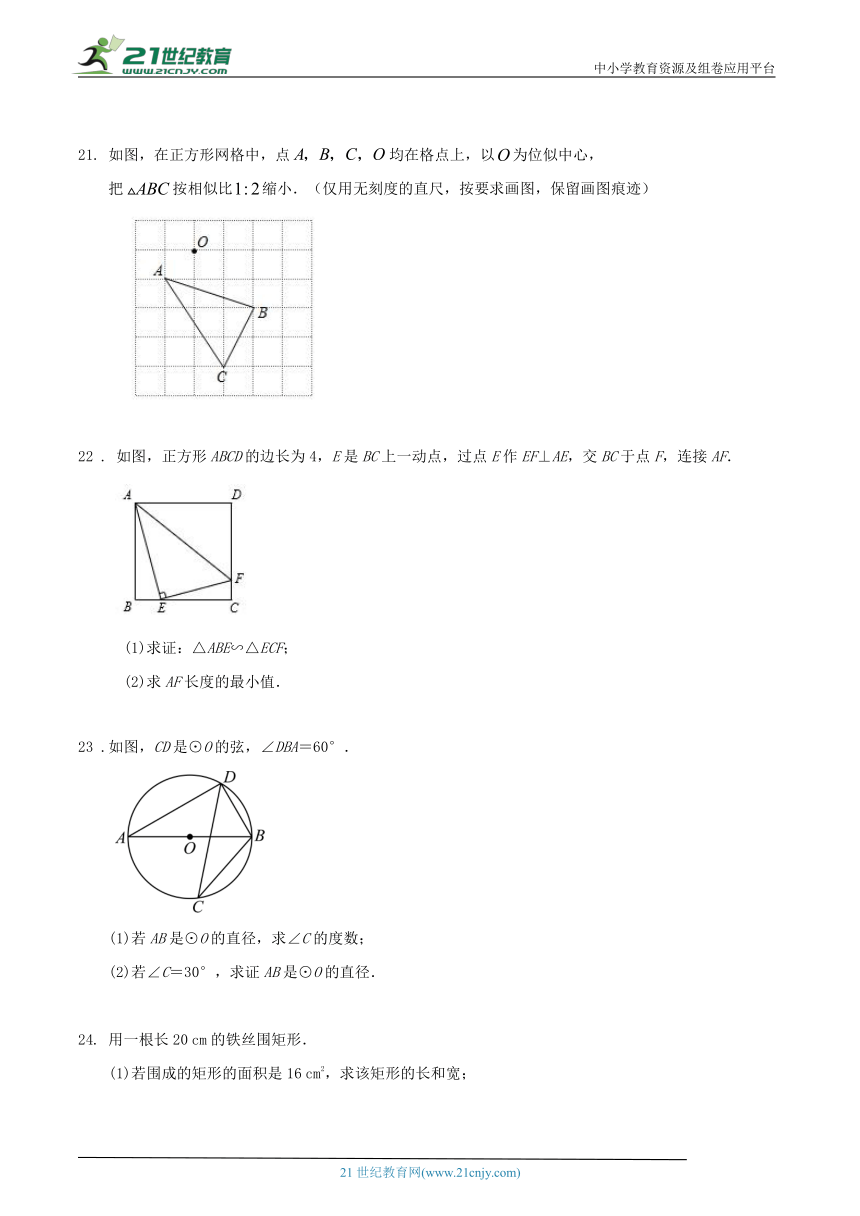
如图,在正方形网格中,点均在格点上,以为位似中心,
把按相似比缩小.(仅用无刻度的直尺,按要求画图,保留画图痕迹)
22 . 如图,正方形ABCD的边长为4,E是BC上一动点,过点E作EF⊥AE,交BC于点F,连接AF.
(1)求证:△ABE∽△ECF;
(2)求AF长度的最小值.
23 .如图,CD是⊙O的弦,∠DBA=60°.
(1)若AB是⊙O的直径,求∠C的度数;
(2)若∠C=30°,求证AB是⊙O的直径.
24. 用一根长20 cm的铁丝围矩形.
(1)若围成的矩形的面积是16 cm2,求该矩形的长和宽;
(2)当长和宽分别为多少时,该矩形的面积最大?最大面积是多少?
25 .(1)如图1,和均为等边三角形,直线和直线交于点F.填空:
①线段,之间的数量关系为________;②的度数为______.
(2)如图2所示,和均为等腰直角三角形,,
直线和直线交于点F,请判断的度数及线段,之间的数量关系,并说明理由.
(3)如图3所示,和均为直角三角形,,,当点B在线段的延长线上时,求线段和的长度.
如图,已知直线与轴交于点,与轴交于点,
抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,
求四边形面积的最大值及此时点的坐标;
若点在抛物线对称轴上,点为任意一点,是否存在点、,
使以点,,,为顶点的四边形是以为对角线的菱形?
若存在,请直接写出,两点的坐标,若不存在,请说明理由.
2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题 解析
一、选择题(本大题共6小题,每小题2分,共12分.)
1.二次函数y=3(x+1)2-2的图像的顶点坐标是( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
【答案】A
【分析】根据二次函数顶点式,顶点为:(h,k),可知题中函数的顶点为(-1,-2)
【详解】解:由题意得,二次函数y=3(x+1)2-2的图像的顶点坐标为(-1,-2).
故选:A.
2. 已知一元二次方程x2-8x+c=0有一个根为2,则另一个根为( )
A.10 B.6 C.8 D.-2
【答案】B
【分析】设方程的另一个根为t,利用两根之和为8得到2+t=8,然后解关于t的方程即可.
【详解】解:设方程的另一个根为t,
根据题意得2+t=8,
解得t=6,
即方程的另一个根为6.
故选:B.
3 .某校开展创建“书香校园”的活动,活动期间对某班位学生所阅读书籍数量的情况进行了统计,
并得到如下所示的统计表,则这组数据的中位数和众数分别是( )
阅读书籍数量 本 本 本 本以上
人数(单位:人)
A., B., C., D.,
【答案】C
【分析】根据众数和中位数的定义,结合表格和选项选出正确答案即可.
【详解】解:一共个数据,这组数据按照从小到大的顺序排列处在第,位的都是,
则中位数为:,
出现的次数最多,则众数为:.
故选:C.
4 .抛物线y=x2向左平移1个单位,再向上平移2个单位后,
所得抛物线的表达式是( )
A.y=(x+1)2﹣2 B.y=(x﹣1)2+2
C.y=(x﹣1)2﹣2 D.y=(x+1)2+2
【答案】D
【分析】根据二次函数图象的平移规律(左加右减,上加下减)进行解答即可.
【详解】抛物线y=x2向左平移1个单位,再向上平移2个单位得y=(x+1)2+2.
故选:D.
如图,A,B,C,D为上的点,且直线与夹角为.
若,,的长分别为,和,则的半径是( )
A. 4 B. C. 5 D.
【答案】A
【解析】
【分析】延长,与直线交于E,连接,设弧长为所对的圆周角为,
根据题意得出,,利用三角形内角和定理求得,
即可求得弧长为所对的圆心角为,代入弧长公式即可求得的半径.
【详解】解:延长,与直线交于E,连接,
,,的长分别为,和,
的长为,的长为,
设弧长为所对的圆周角为,则,,
,,
,
,
弧长为所对的圆心角为,
,
,
故选:A.
6 .如图,抛物线与x轴交于点(4,0),其对称轴为直线,
结合图像,下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有两个不相等的实数根.
其中正确的结论有( )
A.①④ B.③④ C.①②④ D.①③④
【答案】D
【分析】根据函数图象开口方向和与y轴交点位置判断a和c的正负,
令,得的值,根据开口方向和对称轴判断函数图象的增减性,
根据函数图象与x轴交点的个数判断一元二次方程解的情况.
【详解】解:∵函数图象开口向上,
∴,
∵函数图象与y轴交于负半轴,
∴,
∴,故①正确,
∵对称轴是直线,且与x轴交于点(4,0),
∴与x轴的另一个交点坐标是,
∴当时,,故②错误,
∵对称轴是直线,且开口向上,
∴当时,y随x的增大而增大,故③正确,
∵函数图象与x轴有两个交点坐标,
∴关于x的一元二次方程有两个不相等的实数根,故④正确.
故选:D.
二、填空题(本大题共10小题,每小题2分,共20分,请把答案直接填写在答题卡相应位置上)
7 .如图,一个可以自由转动的圆形转盘被分成4个圆心角为60°和1个圆心角为120°的扇形区域,
并涂上了相应的颜色,随机转动转盘,转盘停止时,指针恰好落在黄色区域的概率是 .
【答案】
【分析】根据黄色所占的面积与圆的面积的比,计算概率即可;
【详解】解:∵黄色所占的总圆心角为120°+60°=180°,
∴黄色所占的面积为半圆的面积,
∴指针恰好落在黄色区域的概率是,
故答案为:;
8. 若二次函数的图象和x轴有交点,则a的取值范围为 .
【答案】且
【分析】利用根的判别式进行计算,“图象和轴有交点”说明.
【详解】解:二次函数的图象和轴有交点,
且,
且.
故答案为:且.
9 .如图,小明在打网球时,使球恰好能打过网(网高0.8m),而且落在离网4m的位置上,
则根据图中的数据可知,球拍击球的高度为________m.
【答案】
【解析】
【分析】根据球网和击球时球拍的垂直线段平行即可知,
根据其相似比即可求解.
【详解】解:,
,
,
,
(米,
故答案为:1.6.
10.在一个不透明的盒子中装有n个除颜色外完全相同的球,其中有4个红球.
若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,
发现摸到红球的频率稳定在左右,则n的值大约为_______
【答案】20
【解析】
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,
可以从比例关系入手,列出方程求解.
【详解】解:由题意可得,,
解得:,
经检验是原方程的根,
11 . 已知二次函数的部分图象如图所示,
则关于x的一元二次方程的解为 .
【答案】
【分析】根据图象可知,二次函数的部分图象经过点(4,0),对称轴为,
根据抛物性的对称性即可求出抛物线与x轴的另一个交点坐标,
抛物线与x轴交点坐标的横坐标即为一元二次方程的根.
【详解】解:根据图象可知,二次函数的部分图象经过点(4,0),
对称轴为,
由抛物线的对称性可知:二次函数与x轴的另一个交点坐标为:
抛物线与x轴交点坐标的横坐标即为一元二次方程的根,
即:;
故答案为:.
12.如图,A、B、C、D、E都是⊙O上的点,=,∠B=118°,则∠D的度数为 °.
【答案】124
【分析】连接 AD ,根据圆心角、弧、弦之间的关系定理得到∠ADC = ∠ADE ,
根据圆内接四边形的性质求出∠ADC ,进而得到答案.
【详解】解:连接 AD ,
∵ ,
∴∠ADC = ∠ADE ,
∵四边形 ABCD 为 O 内接四边形, ∠B =118°,
∴∠ADC =180°- ∠B =180°-118°=62°,
∴∠CDE =2×62°=124°,
故答案为:124
13 .某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
【答案】10%
【分析】设平均每次涨价的百分率为x,根据题意列一元二次方程,解方程求解即可.
【详解】设平均每次涨价的百分率为x,根据题意得,
解得(舍)
平均每次涨价的百分率为
故答案为:
14 . 如图,,,图中阴影部分在数学史上称为“希波克拉底月牙”,
当,时,则阴影部分的面积为 .
【答案】
【分析】本题考查勾股定理和三角形的面积、圆的面积.根据勾股定理求出,
分别求出三个半圆的面积和的面积,即可得出答案.
能把不规则图形的面积转化成规则图形的面积是解题的关键.
【详解】解:在中,,,,
∴,
∴阴影部分的面积为:,
∴阴影部分的面积为.
故答案为:.
15 .如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),
施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,
则脚手架高DE为_________米.
【答案】6
【解析】
【分析】根据DE:EF=3:2,可以先设DE=3a,EF=2a,
然后即可表示出点D的坐标,再根据点D在抛物线y=﹣x2+8上,
即可求得a的值,从而可以得到DE的值.
【详解】解:设DE=3a,EF=2a,
则点D的坐标为(﹣a,3a),
∵点D在抛物线y=﹣x2+8上,
∴3a=﹣a2+8,
解得:a1=2,a2=﹣8(舍去),
∴DE=3a=6(米),
故答案为:6.
16 .如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上
(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
【答案】2﹣或.
【分析】当△ABD∽△DCE时,可能是DA=DE,也可能是ED=EA,
所以要分两种情况求出CE长.
【详解】解:∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADE=45°,
∴∠B=∠C=∠ADE.
∵∠ADB=∠C+∠DAC,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC.
∵∠ADC+∠B+∠BAD=180,∠DEC+∠C+∠CDE=180°,
∴∠ADC+∠B+∠BAD=∠DEC+∠C+∠CDE,
∴∠EDC=∠BAD,
∴△ABD∽△DCE
∵∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
∴△ABD≌△DCE.
∴CD=AB=.
∴BD=2﹣= CE,
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°,
∴此时有∠DEA=90°.
即△ADE为等腰直角三角形.
∴AE=DE=AC=.
∴CE=AC=
当AD=EA时,点D与点B重合,不合题意,所以舍去,
因此CE的长为2﹣或.
故答案为2﹣或.
三、解答题(本大题共11小题,共88分.解答时应写出文字说明、证明过程或演算步骤)
17. 解方程:
(1).
(2).
【答案】(1),
(2),
【分析】(1)先移项,再配方,然后开方得出答案;
(2)先移项,再因式分解,可得答案.
【详解】(1)解:,
,
配方,得,
即.
∴,.
(2)解:
移项,得,
因式分解,得,
即,
∴,.
18 .劳动教育已纳入人才培养全过程,某学校加大投入,建设校园农场,
该农场一种作物的产量两年内从300千克增加到363千克.若平均每年的增产率相同,
求平均每年的增产率.
【答案】平均每年的增产率为10%
【解析】
【分析】根据年均增长率的计算公式,列式计算即可.
【详解】解:设平均每年的增产率为x.
根据题意得:
解得 (不合题意,舍去)
答:平均每年的增产率为10%
19 .为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.
竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)小云抽中B组试题的概率是 ;
(2)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
【答案】(1)
(2)
【分析】(1)直接利用概率公式进行计算即可;
(2)先画树状图求解所有的等可能的结果数有9种,同时可得小云和小敏抽到的是同一组试题的机会有3种,再利用概率公式可得答案.
【详解】(1)解:小云抽中B组试题的概率是
故答案为:
(2)解:画树状图如下:
共有9种等可能的结果,符合条件的有3种,
所以小云和小敏抽到的是同一组试题的概率为
20 .王老师为了选拔一名学生参加数学比赛,
对两名备赛选手进行了10次测验,成绩如下(单位:分):
甲:5,6,6,6,6,6,7,9,9,10
乙:5,6,6,6,7,7,7,7,9,10
选手 平均数 中位数 众数 方差
甲 7 a 6
乙 b 7 c d
(1)以上成绩统计分析表中_______,________,______;
(2)d______(填“>”、<或“=”):
(3)根据以上信息,你认为王老师应该选哪位同学参加比赛,请说明理由.
【答案】(1)6,7,7
(2)
(3)乙同学,理由见解析
【解析】
【分析】(1)根据平均数、众数、中位数的定义即可求出结果;
(2)根据平均数和方差的计算结果求出答案;
(3)比较出甲、乙两位同学的中位数、众数和方差即可.
【小问1详解】
解:甲数据从小到大排列,第5、6位都6,故中位数为;
乙的平均数,
乙的数据中7最多有4个,所以众数,
故答案为:6,7,7;
【小问2详解】
,
,
故答案为:;
【小问3详解】
选择乙同学,理由:
乙同学的中位数和众数都比甲的大,并且乙的方差比甲小,成绩比较稳定.
21 .如图,在正方形网格中,点均在格点上,以为位似中心,
把按相似比缩小.(仅用无刻度的直尺,按要求画图,保留画图痕迹)
【答案】见解析
【解析】
【分析】分别连接、、,再结合网格找出、、的中点,顺次连接即可求解.
【详解】解:如图所示,即为所求;
22 . 如图,正方形ABCD的边长为4,E是BC上一动点,过点E作EF⊥AE,交BC于点F,连接AF.
(1)求证:△ABE∽△ECF;
(2)求AF长度的最小值.
【答案】(1)见解析
(2)5
【分析】(1)先利用等角的余角相等,证得∠BAE=∠CEF,再结合∠B=∠C=90°,即可证得△ABE∽△ECF.
(2) 由勾股定理得,在Rt△ADF中,∠D=90°,.
要求AF长度的最小值,即求DF长度的最小值,也就是求CF长度的最大值即可求解.
【详解】(1)证明:∵ 四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°.
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠CEF=90°,
∴∠BAE=∠CEF.
又∵∠B=∠C=90°,
∴△ABE∽△ECF.
(2)∵△ABE∽△ECF,
∴=,
即CF=.
设CE=x,则BE=4-x.
∴CF==-(x-2)2+1,
当x=2时,CF取最大值1;
此时,DF取最小值3.
当DF=3时,AF取最小值,.
∴AF长度的最小值为5.
23.如图,CD是⊙O的弦,∠DBA=60°.
(1)若AB是⊙O的直径,求∠C的度数;
(2)若∠C=30°,求证AB是⊙O的直径.
【答案】(1)30°;
(2)证明见详解.
【分析】(1)根据圆周角定理得出∠ADB=90°,根据三角形的内角和定理求出∠DAB=30°,
根据圆周角定理得出∠C=∠DAB即可;
(2)根据圆周角定理得出∠A=∠C=30°,再根据∠A+∠DBA=90°,得出结论.
【详解】(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠DBA=90°.
∵∠DBA=60°,
∴∠A=30°.
∴∠C=∠A=30°.
(2)∵∠C=30°,
∴∠A=∠C=30°.
∵∠DBA=60°,
∴∠A+∠DBA=90°.
∴∠ADB=90°.
∴AB是⊙O的直径.
24. 用一根长20 cm的铁丝围矩形.
(1)若围成的矩形的面积是16 cm2,求该矩形的长和宽;
(2)当长和宽分别为多少时,该矩形的面积最大?最大面积是多少?
【答案】(1)长为8 cm,宽为2 cm
(2)当长和宽都是5 cm时,该矩形的面积最大,最大面积是25 cm2
【分析】(1)首先表示矩形的另一边长,进而利用矩形面积求法得出答案;
(2)利用二次函数最值求法得出答案.
【详解】(1)解:设该矩形的一组邻边的长为x cm和cm.
根据题意,得
x=16.
解这个方程,得x1=2,x2=8.
当x=2时,-x=8;
当x=8时,-x=2.
答:该矩形的长为8 cm,宽为2 cm.
(2)解:设该矩形的一组邻边的长为x cm和cm,面积为y cm.
根据题意,得
y=x,
即y=-x2+10x,
配方,得y=-(x-5)2+25,
因为-1<0,
所以当x=5时,y有最大值25.
则-x=10-5=5.
答:当长和宽都是5 cm时,该矩形的面积最大,最大面积是25 cm2
25 .(1)如图1,和均为等边三角形,直线和直线交于点F.填空:
①线段,之间的数量关系为________;②的度数为______.
(2)如图2所示,和均为等腰直角三角形,,
直线和直线交于点F,请判断的度数及线段,之间的数量关系,并说明理由.
(3)如图3所示,和均为直角三角形,,,当点B在线段的延长线上时,求线段和的长度.
【答案】(1)①;②;(2);;
(3);
【分析】(1)①根据证明,即可得出;
②根据全等三角形的性质得出,设交于点O,根据,
结合三角形内角和定理,得出即可得出结果;
(2)证明,可得,,根据三角形的外角得出,,即可得结论;
(3)根据勾股定理求出,根据三角函数求出,
求出,证明,
求出,得出.
【详解】解:(1)①∵和均为等边三角形,
∴,,,
∴,
即,
∴,
∴;
故答案为:;
②∵,
∴,
设交于点O,
∵,
∴,
即.
故答案为:.
(2)结论:, .理由如下:
∵,
∴,
又∵,
∴,
∴,,
∴,
∵,
∴.
(3)在中,,
在中,,
∴,
∵,
∴,
∵,
∴ ,
∴,
∴,
∴.
26 .如图,已知直线与轴交于点,与轴交于点,
抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,
求四边形面积的最大值及此时点的坐标;
若点在抛物线对称轴上,点为任意一点,是否存在点、,
使以点,,,为顶点的四边形是以为对角线的菱形?
若存在,请直接写出,两点的坐标,若不存在,请说明理由.
【答案】(1)
(2)的最大值为,
(3)存在;,
【分析】(1)先求得,,三点的坐标,将抛物线设为交点式,进一步求得结果;
作于,交于,根据点和点坐标可表示出的长,
进而表示出三角形的面积,进而表示出的函数关系式,进一步求得结果;
(3)根据菱形性质可得,进而求得点的坐标,根据菱形性质,进一步求得点坐标.
【详解】(1)解:当时,,
,
当时,,
,
,
对称轴为直线,
,
设抛物线的表达式:,
,
,
抛物线的表达式为:;
(2)解:如图1,
作于,交于,
,,
,
,
,
,
当时,,
当时,,
;
(3)解:设,
以,,,为顶点的四边形是以为对角线的菱形,
,
即:,
,
,
,
,,
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题
一、选择题(本大题共6小题,每小题2分,共12分.)
1. 二次函数y=3(x+1)2-2的图像的顶点坐标是( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
2. 已知一元二次方程x2-8x+c=0有一个根为2,则另一个根为( )
A.10 B.6 C.8 D.-2
某校开展创建“书香校园”的活动,活动期间对某班位学生所阅读书籍数量的情况进行了统计,
并得到如下所示的统计表,则这组数据的中位数和众数分别是( )
阅读书籍数量 本 本 本 本以上
人数(单位:人)
A., B., C., D.,
4 . 抛物线y=x2向左平移1个单位,再向上平移2个单位后,
所得抛物线的表达式是( )
A.y=(x+1)2﹣2 B.y=(x﹣1)2+2
C.y=(x﹣1)2﹣2 D.y=(x+1)2+2
5 .如图,A,B,C,D为上的点,且直线与夹角为.
若,,的长分别为,和,则的半径是( )
A. 4 B. C. 5 D.
6 . 如图,抛物线与x轴交于点(4,0),其对称轴为直线,
结合图像,下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有两个不相等的实数根.
其中正确的结论有( )
A.①④ B.③④ C.①②④ D.①③④
二、填空题(本大题共10小题,每小题2分,共20分,请把答案直接填写在答题卡相应位置上)
7 . 如图,一个可以自由转动的圆形转盘被分成4个圆心角为60°和1个圆心角为120°的扇形区域,
并涂上了相应的颜色,随机转动转盘,转盘停止时,指针恰好落在黄色区域的概率是 .
8. 若二次函数的图象和x轴有交点,则a的取值范围为 .
如图,小明在打网球时,使球恰好能打过网(网高0.8m),而且落在离网4m的位置上,
则根据图中的数据可知,球拍击球的高度为________m.
在一个不透明的盒子中装有n个除颜色外完全相同的球,其中有4个红球.
若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,
发现摸到红球的频率稳定在左右,则n的值大约为_______
11 . 已知二次函数的部分图象如图所示,
则关于x的一元二次方程的解为 .
12 .如图,A、B、C、D、E都是⊙O上的点,=,∠B=118°,则∠D的度数为 °.
13 .某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
14 . 如图,,,图中阴影部分在数学史上称为“希波克拉底月牙”,
当,时,则阴影部分的面积为 .
如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),
施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,
则脚手架高DE为_________米.
如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上
(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
三、解答题(本大题共11小题,共88分.解答时应写出文字说明、证明过程或演算步骤)
17. 解方程:
(1).
(2).
18 .劳动教育已纳入人才培养全过程,某学校加大投入,建设校园农场,
该农场一种作物的产量两年内从300千克增加到363千克.若平均每年的增产率相同,
求平均每年的增产率.
为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.
竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)小云抽中B组试题的概率是 ;
(2)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
王老师为了选拔一名学生参加数学比赛,
对两名备赛选手进行了10次测验,成绩如下(单位:分):
甲:5,6,6,6,6,6,7,9,9,10
乙:5,6,6,6,7,7,7,7,9,10
选手 平均数 中位数 众数 方差
甲 7 a 6
乙 b 7 c d
(1)以上成绩统计分析表中_______,________,______;
(2)d______(填“>”、<或“=”):
(3)根据以上信息,你认为王老师应该选哪位同学参加比赛,请说明理由.
如图,在正方形网格中,点均在格点上,以为位似中心,
把按相似比缩小.(仅用无刻度的直尺,按要求画图,保留画图痕迹)
22 . 如图,正方形ABCD的边长为4,E是BC上一动点,过点E作EF⊥AE,交BC于点F,连接AF.
(1)求证:△ABE∽△ECF;
(2)求AF长度的最小值.
23 .如图,CD是⊙O的弦,∠DBA=60°.
(1)若AB是⊙O的直径,求∠C的度数;
(2)若∠C=30°,求证AB是⊙O的直径.
24. 用一根长20 cm的铁丝围矩形.
(1)若围成的矩形的面积是16 cm2,求该矩形的长和宽;
(2)当长和宽分别为多少时,该矩形的面积最大?最大面积是多少?
25 .(1)如图1,和均为等边三角形,直线和直线交于点F.填空:
①线段,之间的数量关系为________;②的度数为______.
(2)如图2所示,和均为等腰直角三角形,,
直线和直线交于点F,请判断的度数及线段,之间的数量关系,并说明理由.
(3)如图3所示,和均为直角三角形,,,当点B在线段的延长线上时,求线段和的长度.
如图,已知直线与轴交于点,与轴交于点,
抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,
求四边形面积的最大值及此时点的坐标;
若点在抛物线对称轴上,点为任意一点,是否存在点、,
使以点,,,为顶点的四边形是以为对角线的菱形?
若存在,请直接写出,两点的坐标,若不存在,请说明理由.
2023-2024学年九年级第一学期江苏省南京市建邺区期末数学试题 解析
一、选择题(本大题共6小题,每小题2分,共12分.)
1.二次函数y=3(x+1)2-2的图像的顶点坐标是( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
【答案】A
【分析】根据二次函数顶点式,顶点为:(h,k),可知题中函数的顶点为(-1,-2)
【详解】解:由题意得,二次函数y=3(x+1)2-2的图像的顶点坐标为(-1,-2).
故选:A.
2. 已知一元二次方程x2-8x+c=0有一个根为2,则另一个根为( )
A.10 B.6 C.8 D.-2
【答案】B
【分析】设方程的另一个根为t,利用两根之和为8得到2+t=8,然后解关于t的方程即可.
【详解】解:设方程的另一个根为t,
根据题意得2+t=8,
解得t=6,
即方程的另一个根为6.
故选:B.
3 .某校开展创建“书香校园”的活动,活动期间对某班位学生所阅读书籍数量的情况进行了统计,
并得到如下所示的统计表,则这组数据的中位数和众数分别是( )
阅读书籍数量 本 本 本 本以上
人数(单位:人)
A., B., C., D.,
【答案】C
【分析】根据众数和中位数的定义,结合表格和选项选出正确答案即可.
【详解】解:一共个数据,这组数据按照从小到大的顺序排列处在第,位的都是,
则中位数为:,
出现的次数最多,则众数为:.
故选:C.
4 .抛物线y=x2向左平移1个单位,再向上平移2个单位后,
所得抛物线的表达式是( )
A.y=(x+1)2﹣2 B.y=(x﹣1)2+2
C.y=(x﹣1)2﹣2 D.y=(x+1)2+2
【答案】D
【分析】根据二次函数图象的平移规律(左加右减,上加下减)进行解答即可.
【详解】抛物线y=x2向左平移1个单位,再向上平移2个单位得y=(x+1)2+2.
故选:D.
如图,A,B,C,D为上的点,且直线与夹角为.
若,,的长分别为,和,则的半径是( )
A. 4 B. C. 5 D.
【答案】A
【解析】
【分析】延长,与直线交于E,连接,设弧长为所对的圆周角为,
根据题意得出,,利用三角形内角和定理求得,
即可求得弧长为所对的圆心角为,代入弧长公式即可求得的半径.
【详解】解:延长,与直线交于E,连接,
,,的长分别为,和,
的长为,的长为,
设弧长为所对的圆周角为,则,,
,,
,
,
弧长为所对的圆心角为,
,
,
故选:A.
6 .如图,抛物线与x轴交于点(4,0),其对称轴为直线,
结合图像,下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有两个不相等的实数根.
其中正确的结论有( )
A.①④ B.③④ C.①②④ D.①③④
【答案】D
【分析】根据函数图象开口方向和与y轴交点位置判断a和c的正负,
令,得的值,根据开口方向和对称轴判断函数图象的增减性,
根据函数图象与x轴交点的个数判断一元二次方程解的情况.
【详解】解:∵函数图象开口向上,
∴,
∵函数图象与y轴交于负半轴,
∴,
∴,故①正确,
∵对称轴是直线,且与x轴交于点(4,0),
∴与x轴的另一个交点坐标是,
∴当时,,故②错误,
∵对称轴是直线,且开口向上,
∴当时,y随x的增大而增大,故③正确,
∵函数图象与x轴有两个交点坐标,
∴关于x的一元二次方程有两个不相等的实数根,故④正确.
故选:D.
二、填空题(本大题共10小题,每小题2分,共20分,请把答案直接填写在答题卡相应位置上)
7 .如图,一个可以自由转动的圆形转盘被分成4个圆心角为60°和1个圆心角为120°的扇形区域,
并涂上了相应的颜色,随机转动转盘,转盘停止时,指针恰好落在黄色区域的概率是 .
【答案】
【分析】根据黄色所占的面积与圆的面积的比,计算概率即可;
【详解】解:∵黄色所占的总圆心角为120°+60°=180°,
∴黄色所占的面积为半圆的面积,
∴指针恰好落在黄色区域的概率是,
故答案为:;
8. 若二次函数的图象和x轴有交点,则a的取值范围为 .
【答案】且
【分析】利用根的判别式进行计算,“图象和轴有交点”说明.
【详解】解:二次函数的图象和轴有交点,
且,
且.
故答案为:且.
9 .如图,小明在打网球时,使球恰好能打过网(网高0.8m),而且落在离网4m的位置上,
则根据图中的数据可知,球拍击球的高度为________m.
【答案】
【解析】
【分析】根据球网和击球时球拍的垂直线段平行即可知,
根据其相似比即可求解.
【详解】解:,
,
,
,
(米,
故答案为:1.6.
10.在一个不透明的盒子中装有n个除颜色外完全相同的球,其中有4个红球.
若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,
发现摸到红球的频率稳定在左右,则n的值大约为_______
【答案】20
【解析】
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,
可以从比例关系入手,列出方程求解.
【详解】解:由题意可得,,
解得:,
经检验是原方程的根,
11 . 已知二次函数的部分图象如图所示,
则关于x的一元二次方程的解为 .
【答案】
【分析】根据图象可知,二次函数的部分图象经过点(4,0),对称轴为,
根据抛物性的对称性即可求出抛物线与x轴的另一个交点坐标,
抛物线与x轴交点坐标的横坐标即为一元二次方程的根.
【详解】解:根据图象可知,二次函数的部分图象经过点(4,0),
对称轴为,
由抛物线的对称性可知:二次函数与x轴的另一个交点坐标为:
抛物线与x轴交点坐标的横坐标即为一元二次方程的根,
即:;
故答案为:.
12.如图,A、B、C、D、E都是⊙O上的点,=,∠B=118°,则∠D的度数为 °.
【答案】124
【分析】连接 AD ,根据圆心角、弧、弦之间的关系定理得到∠ADC = ∠ADE ,
根据圆内接四边形的性质求出∠ADC ,进而得到答案.
【详解】解:连接 AD ,
∵ ,
∴∠ADC = ∠ADE ,
∵四边形 ABCD 为 O 内接四边形, ∠B =118°,
∴∠ADC =180°- ∠B =180°-118°=62°,
∴∠CDE =2×62°=124°,
故答案为:124
13 .某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
【答案】10%
【分析】设平均每次涨价的百分率为x,根据题意列一元二次方程,解方程求解即可.
【详解】设平均每次涨价的百分率为x,根据题意得,
解得(舍)
平均每次涨价的百分率为
故答案为:
14 . 如图,,,图中阴影部分在数学史上称为“希波克拉底月牙”,
当,时,则阴影部分的面积为 .
【答案】
【分析】本题考查勾股定理和三角形的面积、圆的面积.根据勾股定理求出,
分别求出三个半圆的面积和的面积,即可得出答案.
能把不规则图形的面积转化成规则图形的面积是解题的关键.
【详解】解:在中,,,,
∴,
∴阴影部分的面积为:,
∴阴影部分的面积为.
故答案为:.
15 .如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),
施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,
则脚手架高DE为_________米.
【答案】6
【解析】
【分析】根据DE:EF=3:2,可以先设DE=3a,EF=2a,
然后即可表示出点D的坐标,再根据点D在抛物线y=﹣x2+8上,
即可求得a的值,从而可以得到DE的值.
【详解】解:设DE=3a,EF=2a,
则点D的坐标为(﹣a,3a),
∵点D在抛物线y=﹣x2+8上,
∴3a=﹣a2+8,
解得:a1=2,a2=﹣8(舍去),
∴DE=3a=6(米),
故答案为:6.
16 .如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上
(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
【答案】2﹣或.
【分析】当△ABD∽△DCE时,可能是DA=DE,也可能是ED=EA,
所以要分两种情况求出CE长.
【详解】解:∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADE=45°,
∴∠B=∠C=∠ADE.
∵∠ADB=∠C+∠DAC,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC.
∵∠ADC+∠B+∠BAD=180,∠DEC+∠C+∠CDE=180°,
∴∠ADC+∠B+∠BAD=∠DEC+∠C+∠CDE,
∴∠EDC=∠BAD,
∴△ABD∽△DCE
∵∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
∴△ABD≌△DCE.
∴CD=AB=.
∴BD=2﹣= CE,
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°,
∴此时有∠DEA=90°.
即△ADE为等腰直角三角形.
∴AE=DE=AC=.
∴CE=AC=
当AD=EA时,点D与点B重合,不合题意,所以舍去,
因此CE的长为2﹣或.
故答案为2﹣或.
三、解答题(本大题共11小题,共88分.解答时应写出文字说明、证明过程或演算步骤)
17. 解方程:
(1).
(2).
【答案】(1),
(2),
【分析】(1)先移项,再配方,然后开方得出答案;
(2)先移项,再因式分解,可得答案.
【详解】(1)解:,
,
配方,得,
即.
∴,.
(2)解:
移项,得,
因式分解,得,
即,
∴,.
18 .劳动教育已纳入人才培养全过程,某学校加大投入,建设校园农场,
该农场一种作物的产量两年内从300千克增加到363千克.若平均每年的增产率相同,
求平均每年的增产率.
【答案】平均每年的增产率为10%
【解析】
【分析】根据年均增长率的计算公式,列式计算即可.
【详解】解:设平均每年的增产率为x.
根据题意得:
解得 (不合题意,舍去)
答:平均每年的增产率为10%
19 .为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.
竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)小云抽中B组试题的概率是 ;
(2)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
【答案】(1)
(2)
【分析】(1)直接利用概率公式进行计算即可;
(2)先画树状图求解所有的等可能的结果数有9种,同时可得小云和小敏抽到的是同一组试题的机会有3种,再利用概率公式可得答案.
【详解】(1)解:小云抽中B组试题的概率是
故答案为:
(2)解:画树状图如下:
共有9种等可能的结果,符合条件的有3种,
所以小云和小敏抽到的是同一组试题的概率为
20 .王老师为了选拔一名学生参加数学比赛,
对两名备赛选手进行了10次测验,成绩如下(单位:分):
甲:5,6,6,6,6,6,7,9,9,10
乙:5,6,6,6,7,7,7,7,9,10
选手 平均数 中位数 众数 方差
甲 7 a 6
乙 b 7 c d
(1)以上成绩统计分析表中_______,________,______;
(2)d______(填“>”、<或“=”):
(3)根据以上信息,你认为王老师应该选哪位同学参加比赛,请说明理由.
【答案】(1)6,7,7
(2)
(3)乙同学,理由见解析
【解析】
【分析】(1)根据平均数、众数、中位数的定义即可求出结果;
(2)根据平均数和方差的计算结果求出答案;
(3)比较出甲、乙两位同学的中位数、众数和方差即可.
【小问1详解】
解:甲数据从小到大排列,第5、6位都6,故中位数为;
乙的平均数,
乙的数据中7最多有4个,所以众数,
故答案为:6,7,7;
【小问2详解】
,
,
故答案为:;
【小问3详解】
选择乙同学,理由:
乙同学的中位数和众数都比甲的大,并且乙的方差比甲小,成绩比较稳定.
21 .如图,在正方形网格中,点均在格点上,以为位似中心,
把按相似比缩小.(仅用无刻度的直尺,按要求画图,保留画图痕迹)
【答案】见解析
【解析】
【分析】分别连接、、,再结合网格找出、、的中点,顺次连接即可求解.
【详解】解:如图所示,即为所求;
22 . 如图,正方形ABCD的边长为4,E是BC上一动点,过点E作EF⊥AE,交BC于点F,连接AF.
(1)求证:△ABE∽△ECF;
(2)求AF长度的最小值.
【答案】(1)见解析
(2)5
【分析】(1)先利用等角的余角相等,证得∠BAE=∠CEF,再结合∠B=∠C=90°,即可证得△ABE∽△ECF.
(2) 由勾股定理得,在Rt△ADF中,∠D=90°,.
要求AF长度的最小值,即求DF长度的最小值,也就是求CF长度的最大值即可求解.
【详解】(1)证明:∵ 四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°.
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠CEF=90°,
∴∠BAE=∠CEF.
又∵∠B=∠C=90°,
∴△ABE∽△ECF.
(2)∵△ABE∽△ECF,
∴=,
即CF=.
设CE=x,则BE=4-x.
∴CF==-(x-2)2+1,
当x=2时,CF取最大值1;
此时,DF取最小值3.
当DF=3时,AF取最小值,.
∴AF长度的最小值为5.
23.如图,CD是⊙O的弦,∠DBA=60°.
(1)若AB是⊙O的直径,求∠C的度数;
(2)若∠C=30°,求证AB是⊙O的直径.
【答案】(1)30°;
(2)证明见详解.
【分析】(1)根据圆周角定理得出∠ADB=90°,根据三角形的内角和定理求出∠DAB=30°,
根据圆周角定理得出∠C=∠DAB即可;
(2)根据圆周角定理得出∠A=∠C=30°,再根据∠A+∠DBA=90°,得出结论.
【详解】(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠DBA=90°.
∵∠DBA=60°,
∴∠A=30°.
∴∠C=∠A=30°.
(2)∵∠C=30°,
∴∠A=∠C=30°.
∵∠DBA=60°,
∴∠A+∠DBA=90°.
∴∠ADB=90°.
∴AB是⊙O的直径.
24. 用一根长20 cm的铁丝围矩形.
(1)若围成的矩形的面积是16 cm2,求该矩形的长和宽;
(2)当长和宽分别为多少时,该矩形的面积最大?最大面积是多少?
【答案】(1)长为8 cm,宽为2 cm
(2)当长和宽都是5 cm时,该矩形的面积最大,最大面积是25 cm2
【分析】(1)首先表示矩形的另一边长,进而利用矩形面积求法得出答案;
(2)利用二次函数最值求法得出答案.
【详解】(1)解:设该矩形的一组邻边的长为x cm和cm.
根据题意,得
x=16.
解这个方程,得x1=2,x2=8.
当x=2时,-x=8;
当x=8时,-x=2.
答:该矩形的长为8 cm,宽为2 cm.
(2)解:设该矩形的一组邻边的长为x cm和cm,面积为y cm.
根据题意,得
y=x,
即y=-x2+10x,
配方,得y=-(x-5)2+25,
因为-1<0,
所以当x=5时,y有最大值25.
则-x=10-5=5.
答:当长和宽都是5 cm时,该矩形的面积最大,最大面积是25 cm2
25 .(1)如图1,和均为等边三角形,直线和直线交于点F.填空:
①线段,之间的数量关系为________;②的度数为______.
(2)如图2所示,和均为等腰直角三角形,,
直线和直线交于点F,请判断的度数及线段,之间的数量关系,并说明理由.
(3)如图3所示,和均为直角三角形,,,当点B在线段的延长线上时,求线段和的长度.
【答案】(1)①;②;(2);;
(3);
【分析】(1)①根据证明,即可得出;
②根据全等三角形的性质得出,设交于点O,根据,
结合三角形内角和定理,得出即可得出结果;
(2)证明,可得,,根据三角形的外角得出,,即可得结论;
(3)根据勾股定理求出,根据三角函数求出,
求出,证明,
求出,得出.
【详解】解:(1)①∵和均为等边三角形,
∴,,,
∴,
即,
∴,
∴;
故答案为:;
②∵,
∴,
设交于点O,
∵,
∴,
即.
故答案为:.
(2)结论:, .理由如下:
∵,
∴,
又∵,
∴,
∴,,
∴,
∵,
∴.
(3)在中,,
在中,,
∴,
∵,
∴,
∵,
∴ ,
∴,
∴,
∴.
26 .如图,已知直线与轴交于点,与轴交于点,
抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,
求四边形面积的最大值及此时点的坐标;
若点在抛物线对称轴上,点为任意一点,是否存在点、,
使以点,,,为顶点的四边形是以为对角线的菱形?
若存在,请直接写出,两点的坐标,若不存在,请说明理由.
【答案】(1)
(2)的最大值为,
(3)存在;,
【分析】(1)先求得,,三点的坐标,将抛物线设为交点式,进一步求得结果;
作于,交于,根据点和点坐标可表示出的长,
进而表示出三角形的面积,进而表示出的函数关系式,进一步求得结果;
(3)根据菱形性质可得,进而求得点的坐标,根据菱形性质,进一步求得点坐标.
【详解】(1)解:当时,,
,
当时,,
,
,
对称轴为直线,
,
设抛物线的表达式:,
,
,
抛物线的表达式为:;
(2)解:如图1,
作于,交于,
,,
,
,
,
,
当时,,
当时,,
;
(3)解:设,
以,,,为顶点的四边形是以为对角线的菱形,
,
即:,
,
,
,
,,
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
