苏教版五年级上册数学《小数的意义和性质》(课件)(共20张PPT)
文档属性
| 名称 | 苏教版五年级上册数学《小数的意义和性质》(课件)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 547.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 14:41:32 | ||
图片预览







文档简介
(共20张PPT)
第三单元
小数的意义与性质
一、小数的意义和读写方法。
(1)、小数的意义:分母是10、100、1000……的分数都可以用小数表示。一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几....
(2)、小数的写法:写小数时,先写整数部分,小数点写在个位的右下角,小数部分顺次写出每一个数位上的数字。
(3)、小数的读法:读小数时,整数部分按整数的读法来读,小数点读作“点”,小数部分顺次读出每一个数位上的数字。
一、小数的意义和读写方法。
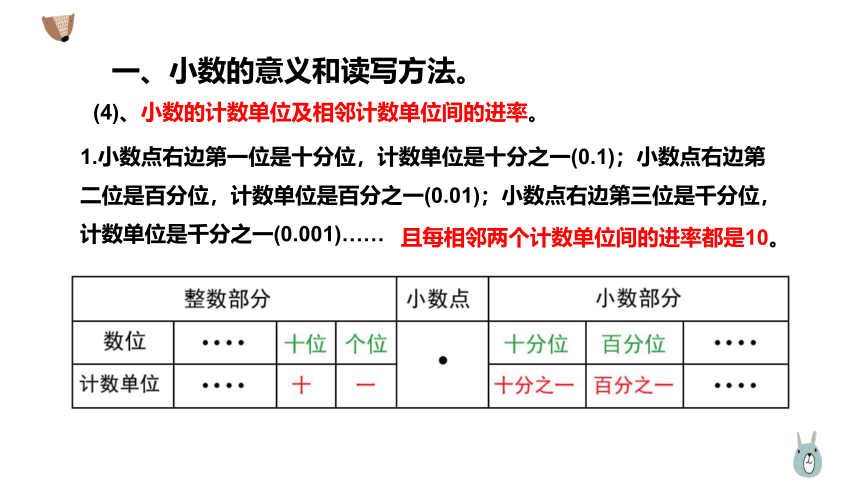
(4)、小数的计数单位及相邻计数单位间的进率。
1.小数点右边第一位是十分位,计数单位是十分之一(0.1);小数点右边第二位是百分位,计数单位是百分之一(0.01);小数点右边第三位是千分位,计数单位是千分之一(0.001)……
且每相邻两个计数单位间的进率都是10。
小数与分数的相互转化:一位小数就是十分之几,两位小数就是百分之几,
三位小数就是千分之几·····, 分数化成小数则反之:分母是10、100、
1000····的分数才能化成小数;十分之几就是一位小数;百分之几就是
两位小数;千分之几就是三位小数···· 。
一、小数的意义与性质 。
例: 1角钱等于几分之几元?写成小数是多少元?5角钱呢 你是怎么理解的?
解析、把1元平均分成10份,每份是1角钱。所以1角就等于1元的,
则1角=( )元 = ( )元。同理得5角=( )元 = ( )元。
0.1
0.5
例题讲解:
例1: 1厘米用分数表示是( )米,用小数表示是( )米,8厘米是1米的( ),用小数表示是( )米,5分米用小数表示是( )米。
0.01
0.08
0.5
例2: 60.06中整数部分的“6”在( )位上,表示6个( );小数部分的“6”在( )上,表示6个( )。
十
10
百分
例3: 由4个一,7个十分之一和4个百分之一组成的小数是( )。
4.74
例4: 0.9里面有( )个十分之一,0.07里面有( )个百分之一。
9
7
例5: 6个0.001是( ),6个( )是0.06。
例6: 7.38米=( )米( )分米( )厘米。
0.006
0.01
7
3
8
例题讲解:
例1: 7个10、6个0.1和2个0.001组成的数是( )。
70.602
例2: 28个一和28个百分之一合起来是( )
28.28
例3: 一个小数,百位上和百分位上都是6,其余的数位上都是0,
这个小数是( )。
600.06
例4: 由3个10、7个0.1和5个0.001组成的数是( )。
30.705
一、小数的意义和读写方法。
(5)、小数的计数单位:
一位小数的计数单位就是0.1;两位小数的计数单位就是0.01;三位小数的计数单位就是0.001·····。例:8.09是两位小数,所以8.09的计数单位是0.01。
例1、连连看。
0.45
1.45 45个百分之一
0.456 1和45个0.01
4.5 4和5个0.1
例题演练:
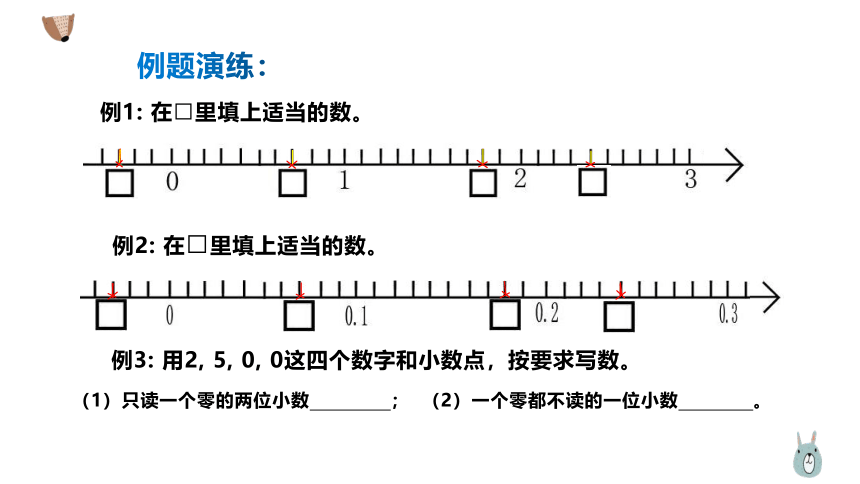
例1: 在□里填上适当的数。
例2: 在□里填上适当的数。
例3: 用2, 5, 0, 0这四个数字和小数点,按要求写数。
(1)只读一个零的两位小数 ; (2)一个零都不读的一位小数 。
例题演练:
例4: 写出下面横线上的数。
(1)妈妈的身高为一点六八米。 ( )
(2)南京长江大桥全长六点七七千米。 ( )
(3)一种飞机的速度是每分钟五点七千米。 ( )
(4)一只麻雀重零点零二千克。 ( )
1.68
6.77
5.7
0.02
一、小数的性质。
(6)、小数的性质:
小数的末尾添上“0”或去掉“0”,小数的大小不变。但是我们不能说小数点的后面添上“0”或去掉“0”小数的大小不变,这句话是不对的。
例1、不改变数的大小,把下面各数改写成三位小数。
0.05= 8= 16.40000=
例2、化简下面的小数。
0.900= 0.8070= 0.0500= 10.030= 7.0060= 30.70= 0.050= 0.60= 1.850= 0.3400=
一、小数的性质。
例3、在( )里填上合适的两位小数。
5角=( )元 5分=( )元
6元9角=( )元 3元零8分=( )元
拓展知识点:
将一个小数的末尾添上0后,小数的大小不变,但小数的计数单位变小了,例:1.3的计数单位是0.1,而1.30的计数单位是0.01。
将一个小数的末尾去掉0后,小数的大小不变,但小数的计数单位变大了,例:2.30的计数单位是0.01,而2.3的计数单位是0.1。
一、小数的性质。
(7)、小数的大小比较:
小数比较大小时,从小数的整数部分开始,整数部分大的那个小数就大;如果整数部分一样,就看十分位,十分位上数大的那个小数就大;如果十分位一样,就看百分位,百分位上数大的那个小数就大······
例1、下面的小数,各在哪两个相邻的整数之间?
( )<2.6<( ) ( )<12.09<( ) ( )<8.08<( )
( )<100.5<( ) ( )<4.005<( ) ( )<80.15<( )
例题演练:
例2: 把0.7, 8.65, 0.499, 2.03按从大到小的顺序排列 。
例3:把0.63, 0.633, 0.603, 0.36, 3.6 按从小到大的顺序排列。
例4: 下面的□里最小能填几
3.17<□.6 0.802<0.8□1
例5: 下面□的里最大能填几
0.□6>0.58 4.□7>4.38 0.9□<0.95
3.42>3.4□ 2.66>□.55 0.80□<0.902
一、小数的性质。
(8)、根据错误的读法推出原来的小数。
例:小马虎在读一个小数时,漏看了小数点,结果读成了六万五千零四。
原来的小数读出两个“零”,原来的小数是多少?
变式:小明读一个小数时,没有看到小数点,结果读成了四万零四。
(1)如果读原来的小数时只读出一个“零”,那么原来的小数是多少
(2)如果读原来的小数时一个“零”也没读出,那么原来的小数是多少
一、小数的性质。
(9)、运用小数的读、写法按要求组小数的问题。
例: 用7,8,0,0这四个数字和小数点组成小数,使组成的小数符合下面的要求。
(1)只读一个“零”的两位小数。 (2)一个“零”都不读的一位小数。
变式: 用0,0,5,8和小数点组成符合下面要求的数。
(1)只读一个“零”的两位小数有( )个,分别是( )。
(2)一个“零”都不读的一位小数有( )个,分别是( )。
(3)读出两个“零”的三位小数有( )。 (写出2个)
4
2
一、小数的性质。
(10)、任意两个计数单位间的进率与小数的组成。
例: 百分之一和万分之一间的进率是( )。
变式1: 0.1里面有( )个0.0001,1里面有( )个0.01。
变式2:80.08中左边的“8”所表示的数是右边的“8”所表示的数的( )倍。
100
1000
100
1000
例题演练:
例1: 由5个10、6个0.1和7个0.001组成的数是( )。
例2: 60.105是由( )个10、( )个0.1和( )个0.001组成的。
例3: 由3个100、2个1和12个0.01组成的数是( ).
例4: 5.8里面有( )个0.01, 有( )个0.001。
例5: 0.6里面有( )个0.1,也可以说有( )个0.01,
还可以说有( )个0.001。
一、小数的性质。
(11)、用“万”“亿”“一”作单位的数的相互改写。
例: 将632.6万先改写成用“一”作单位的数,再改写成用“亿”作单位的数。
变式1: 0.97亿=( )万 =( )
变式2:4500万=( )亿=( )
变式3:把下列各数按从大到小的顺序排列。
9050万 5900000 0.095亿 9500
一、小数的性质。
(12)、最值法在小数近似数中的应用。
例: 想一想,□里可以填哪些数字。
(1) 780.9□5 ≈ 780.9,□里可以填 ( )。
(2) 780.9 □5 ≈ 781.0,里可以填 ( )。
变式1:□里最大能填几 。
4.23□ ≈ 4.24 5.88□ ≈ 5.88 19.7□ ≈ 19.7 4.8□ ≈ 4.9
9□8470000 ≈ 10亿, □里可以填( ); 13□467≈13万, □里可以填( )。
一、小数的性质。
(12)、运用逆推法解决求“四舍五入”前的数值问题。
例1: 百分位上的数字“四舍”后是3.6的两位小数有哪些 百分位上的数字“五入”后是5.0的两位小数有哪些
例2: 百分位上的数字“四舍”后是2.8的两位小数有哪些 百分位上的数字“五入”后是3.0的两位小数有哪些
第三单元
小数的意义与性质
一、小数的意义和读写方法。
(1)、小数的意义:分母是10、100、1000……的分数都可以用小数表示。一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几....
(2)、小数的写法:写小数时,先写整数部分,小数点写在个位的右下角,小数部分顺次写出每一个数位上的数字。
(3)、小数的读法:读小数时,整数部分按整数的读法来读,小数点读作“点”,小数部分顺次读出每一个数位上的数字。
一、小数的意义和读写方法。
(4)、小数的计数单位及相邻计数单位间的进率。
1.小数点右边第一位是十分位,计数单位是十分之一(0.1);小数点右边第二位是百分位,计数单位是百分之一(0.01);小数点右边第三位是千分位,计数单位是千分之一(0.001)……
且每相邻两个计数单位间的进率都是10。
小数与分数的相互转化:一位小数就是十分之几,两位小数就是百分之几,
三位小数就是千分之几·····, 分数化成小数则反之:分母是10、100、
1000····的分数才能化成小数;十分之几就是一位小数;百分之几就是
两位小数;千分之几就是三位小数···· 。
一、小数的意义与性质 。
例: 1角钱等于几分之几元?写成小数是多少元?5角钱呢 你是怎么理解的?
解析、把1元平均分成10份,每份是1角钱。所以1角就等于1元的,
则1角=( )元 = ( )元。同理得5角=( )元 = ( )元。
0.1
0.5
例题讲解:
例1: 1厘米用分数表示是( )米,用小数表示是( )米,8厘米是1米的( ),用小数表示是( )米,5分米用小数表示是( )米。
0.01
0.08
0.5
例2: 60.06中整数部分的“6”在( )位上,表示6个( );小数部分的“6”在( )上,表示6个( )。
十
10
百分
例3: 由4个一,7个十分之一和4个百分之一组成的小数是( )。
4.74
例4: 0.9里面有( )个十分之一,0.07里面有( )个百分之一。
9
7
例5: 6个0.001是( ),6个( )是0.06。
例6: 7.38米=( )米( )分米( )厘米。
0.006
0.01
7
3
8
例题讲解:
例1: 7个10、6个0.1和2个0.001组成的数是( )。
70.602
例2: 28个一和28个百分之一合起来是( )
28.28
例3: 一个小数,百位上和百分位上都是6,其余的数位上都是0,
这个小数是( )。
600.06
例4: 由3个10、7个0.1和5个0.001组成的数是( )。
30.705
一、小数的意义和读写方法。
(5)、小数的计数单位:
一位小数的计数单位就是0.1;两位小数的计数单位就是0.01;三位小数的计数单位就是0.001·····。例:8.09是两位小数,所以8.09的计数单位是0.01。
例1、连连看。
0.45
1.45 45个百分之一
0.456 1和45个0.01
4.5 4和5个0.1
例题演练:
例1: 在□里填上适当的数。
例2: 在□里填上适当的数。
例3: 用2, 5, 0, 0这四个数字和小数点,按要求写数。
(1)只读一个零的两位小数 ; (2)一个零都不读的一位小数 。
例题演练:
例4: 写出下面横线上的数。
(1)妈妈的身高为一点六八米。 ( )
(2)南京长江大桥全长六点七七千米。 ( )
(3)一种飞机的速度是每分钟五点七千米。 ( )
(4)一只麻雀重零点零二千克。 ( )
1.68
6.77
5.7
0.02
一、小数的性质。
(6)、小数的性质:
小数的末尾添上“0”或去掉“0”,小数的大小不变。但是我们不能说小数点的后面添上“0”或去掉“0”小数的大小不变,这句话是不对的。
例1、不改变数的大小,把下面各数改写成三位小数。
0.05= 8= 16.40000=
例2、化简下面的小数。
0.900= 0.8070= 0.0500= 10.030= 7.0060= 30.70= 0.050= 0.60= 1.850= 0.3400=
一、小数的性质。
例3、在( )里填上合适的两位小数。
5角=( )元 5分=( )元
6元9角=( )元 3元零8分=( )元
拓展知识点:
将一个小数的末尾添上0后,小数的大小不变,但小数的计数单位变小了,例:1.3的计数单位是0.1,而1.30的计数单位是0.01。
将一个小数的末尾去掉0后,小数的大小不变,但小数的计数单位变大了,例:2.30的计数单位是0.01,而2.3的计数单位是0.1。
一、小数的性质。
(7)、小数的大小比较:
小数比较大小时,从小数的整数部分开始,整数部分大的那个小数就大;如果整数部分一样,就看十分位,十分位上数大的那个小数就大;如果十分位一样,就看百分位,百分位上数大的那个小数就大······
例1、下面的小数,各在哪两个相邻的整数之间?
( )<2.6<( ) ( )<12.09<( ) ( )<8.08<( )
( )<100.5<( ) ( )<4.005<( ) ( )<80.15<( )
例题演练:
例2: 把0.7, 8.65, 0.499, 2.03按从大到小的顺序排列 。
例3:把0.63, 0.633, 0.603, 0.36, 3.6 按从小到大的顺序排列。
例4: 下面的□里最小能填几
3.17<□.6 0.802<0.8□1
例5: 下面□的里最大能填几
0.□6>0.58 4.□7>4.38 0.9□<0.95
3.42>3.4□ 2.66>□.55 0.80□<0.902
一、小数的性质。
(8)、根据错误的读法推出原来的小数。
例:小马虎在读一个小数时,漏看了小数点,结果读成了六万五千零四。
原来的小数读出两个“零”,原来的小数是多少?
变式:小明读一个小数时,没有看到小数点,结果读成了四万零四。
(1)如果读原来的小数时只读出一个“零”,那么原来的小数是多少
(2)如果读原来的小数时一个“零”也没读出,那么原来的小数是多少
一、小数的性质。
(9)、运用小数的读、写法按要求组小数的问题。
例: 用7,8,0,0这四个数字和小数点组成小数,使组成的小数符合下面的要求。
(1)只读一个“零”的两位小数。 (2)一个“零”都不读的一位小数。
变式: 用0,0,5,8和小数点组成符合下面要求的数。
(1)只读一个“零”的两位小数有( )个,分别是( )。
(2)一个“零”都不读的一位小数有( )个,分别是( )。
(3)读出两个“零”的三位小数有( )。 (写出2个)
4
2
一、小数的性质。
(10)、任意两个计数单位间的进率与小数的组成。
例: 百分之一和万分之一间的进率是( )。
变式1: 0.1里面有( )个0.0001,1里面有( )个0.01。
变式2:80.08中左边的“8”所表示的数是右边的“8”所表示的数的( )倍。
100
1000
100
1000
例题演练:
例1: 由5个10、6个0.1和7个0.001组成的数是( )。
例2: 60.105是由( )个10、( )个0.1和( )个0.001组成的。
例3: 由3个100、2个1和12个0.01组成的数是( ).
例4: 5.8里面有( )个0.01, 有( )个0.001。
例5: 0.6里面有( )个0.1,也可以说有( )个0.01,
还可以说有( )个0.001。
一、小数的性质。
(11)、用“万”“亿”“一”作单位的数的相互改写。
例: 将632.6万先改写成用“一”作单位的数,再改写成用“亿”作单位的数。
变式1: 0.97亿=( )万 =( )
变式2:4500万=( )亿=( )
变式3:把下列各数按从大到小的顺序排列。
9050万 5900000 0.095亿 9500
一、小数的性质。
(12)、最值法在小数近似数中的应用。
例: 想一想,□里可以填哪些数字。
(1) 780.9□5 ≈ 780.9,□里可以填 ( )。
(2) 780.9 □5 ≈ 781.0,里可以填 ( )。
变式1:□里最大能填几 。
4.23□ ≈ 4.24 5.88□ ≈ 5.88 19.7□ ≈ 19.7 4.8□ ≈ 4.9
9□8470000 ≈ 10亿, □里可以填( ); 13□467≈13万, □里可以填( )。
一、小数的性质。
(12)、运用逆推法解决求“四舍五入”前的数值问题。
例1: 百分位上的数字“四舍”后是3.6的两位小数有哪些 百分位上的数字“五入”后是5.0的两位小数有哪些
例2: 百分位上的数字“四舍”后是2.8的两位小数有哪些 百分位上的数字“五入”后是3.0的两位小数有哪些
