北师大版五年级下册数学整理与复习 长方体(课件)(共24张ppt)
文档属性
| 名称 | 北师大版五年级下册数学整理与复习 长方体(课件)(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 15:08:25 | ||
图片预览





文档简介
北师版数学五年级(下)
长方体
整理与复习
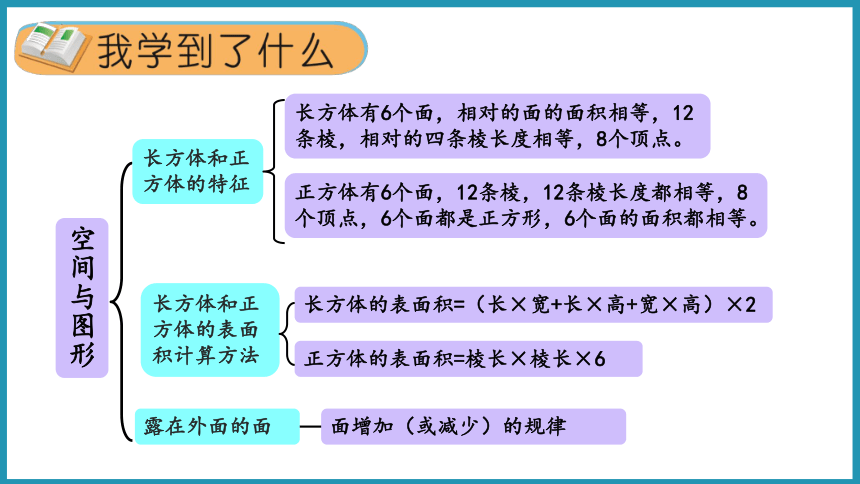
长方体和正方体的表面积计算方法
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
空间与图形
长方体和正方体的特征
露在外面的面
面增加(或减少)的规律
长方体有6个面,相对的面的面积相等,12条棱,相对的四条棱长度相等,8个顶点。
正方体有6个面,12条棱,12条棱长度都相等,8个顶点,6个面都是正方形,6个面的面积都相等。
我们会算长方体和正方体的体积了,怎么算球体的体积呢?
长方体和正方体的体积与棱长有关,球体的体积与球的半径有关。球的体积计算公式是V=????????????????????,R是球的半径。这个公式同学们在以后的学习中会学到。
?
要点1:长方体与正方体的特征
名称
联系
长方体
正方体
6个面
相同点
不同点
面的形状
面的大小
棱的长度
长方体
正方体
正方体是特殊的长方体
长方形;也可能两个相对面是正方形
相对的面的面积相等
12条棱分3组,每组中棱的长度相等
6个面都是正方形
6个面面积都相等
12条棱长都相等
8个顶点
12条棱
知识回顾
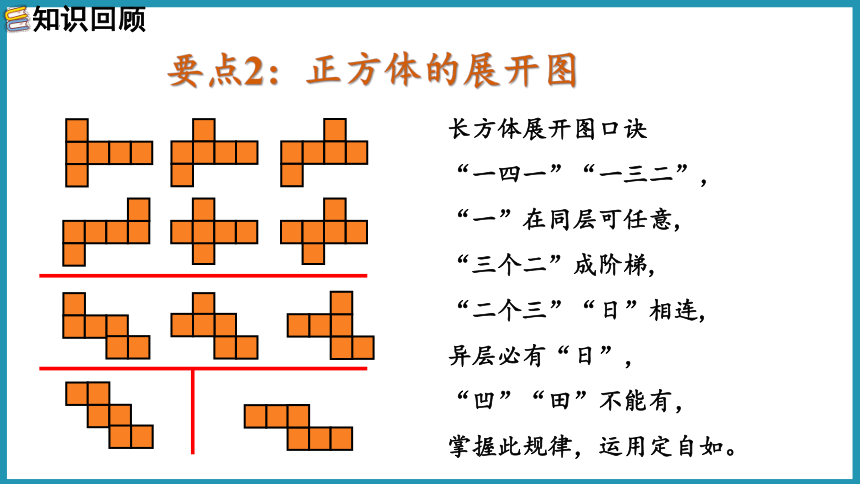
要点2:正方体的展开图
长方体展开图口诀
“一四一”“一三二”,
“一”在同层可任意,
“三个二”成阶梯,
“二个三”“日”相连,
异层必有“日”,
“凹”“田”不能有,
掌握此规律,运用定自如。
知识回顾
要点3:长方体和正方体的表面积
长方体的表面积 =(长×宽+长×高+宽×高)×2
=长×宽×2 +长×高×2 +宽×高×2
正方体的表面积 =棱长×棱长×6
=一个面的面积×6
长方体或正方体6个面的总面积,叫作它的表面积。
注意:在求物体表面积的时候,要根据具体的情况决定求几个面的面积之和。
知识回顾
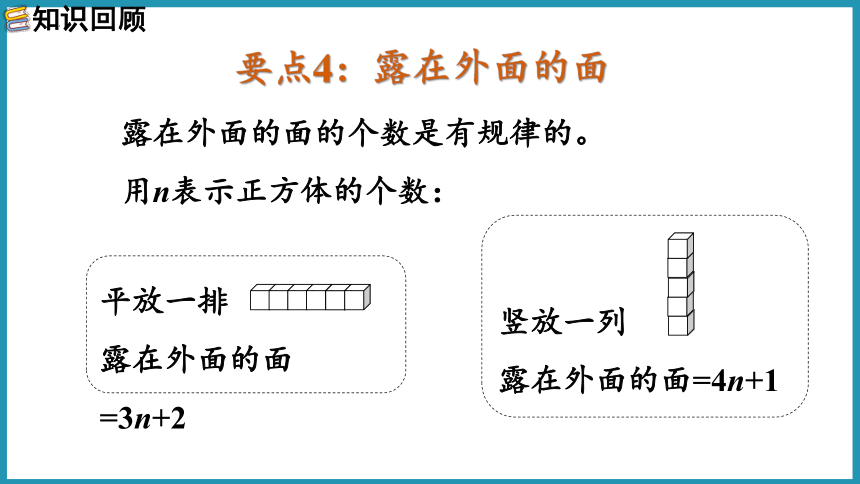
要点4:露在外面的面
露在外面的面的个数是有规律的。?
用n表示正方体的个数:??
平放一排?????
露在外面的面=3n+2?
竖放一列?????
露在外面的面=4n+1
知识回顾
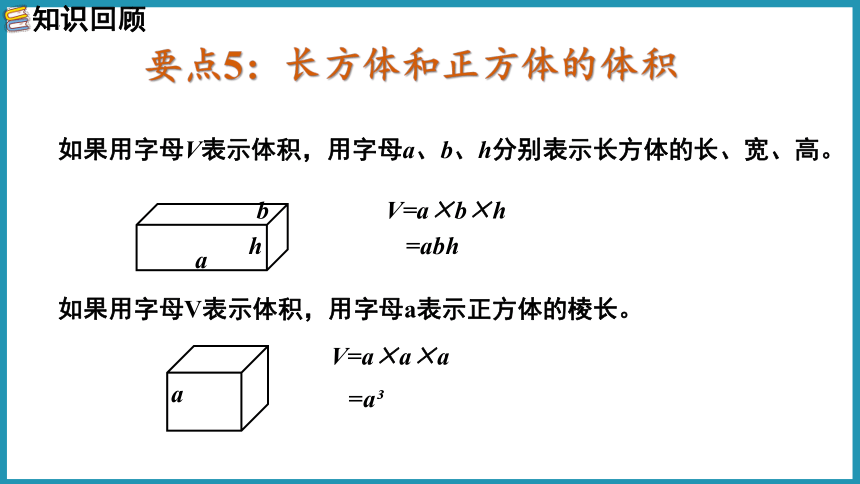
要点5:长方体和正方体的体积
如果用字母V表示体积,用字母a、b、h分别表示长方体的长、宽、高。
V=a×b×h
=abh
a
b
h
如果用字母V表示体积,用字母a表示正方体的棱长。
V=a×a×a
=a?
a
知识回顾
高级单位变为低级单位:数字会变大,高级单位的数×进率
低级单位变为高级单位:数字会变小,低级单位的数÷进率
1m3=1000dm3
1dm3=1000cm3
1L =1000mL
1L=1dm3
1mL=1cm3
1m3=1000000cm3
要点6:单位换算
知识回顾
1.想一想,填一填。
(1)一个药水瓶的容积是200( 毫升 ),一个仓库的占地
面积是300( 平方米 ),一个集装箱的体积约是40( 立
方米 )。
(2)280 mL=( 280 )cm3=( 0.28 )dm3
毫升
平方米
立
方米
280
0.28
6.24 m3=( 6240 )dm3
(3)有5个棱长是2 dm的正方体堆在墙角处,露在外面的面积
是( 44 )dm2。
6240
44
课堂练习
2.选一选。
(1)若一个长方体长3 cm,宽3 cm,高5 cm,则棱长是3 cm
的棱有( C )条。
A.4
B.6
C.8
D.18
(2)下列展开图沿虚线折叠后不能围成一个长方体的是
( B )。
A
B
C
D
C
B
(3)①是由36个完全相同的小正方体堆成的,把①推倒后
变成②,再利用这堆小正方体在③上4个4个地往上堆成一
栋“大楼”,这栋“大楼”的层数为( D )层。
A.12
B.4
C.6
D.9
D
3.一个长方体水池,底面长12 dm,宽6 dm。如果要向这个
水池里注入2 dm高的水,需要多少升水?
12×6×2=144(dm3)
144 dm3=144 L
答:需要144 L水。
4.李师傅想焊接一个无盖长方体铁皮煤箱,准备从如图8块
废旧铁皮中挑选5块使用,李师傅应该挑选哪5块铁皮?
(铁板厚度忽略不计)(单位:cm)
答:李师傅应该选③④⑤⑥⑦这5块铁皮。
=(12×10+12×8+10×8)×2
S=(ab+ah+bh)×2
=(120+96+80)×2
= 296×2
= 592(cm?)
5.右面是一个长方体盒子的展开图。(单位:厘米)
(1)长方体盒子的表面积是多少平方厘米?
答:盒子的表面积是592平方厘米。
=12×10×8
=120×8
=960(cm?)
V=abh
(2)长方体的体积是多少立方厘米?
答:长方体的体积是960立方厘米。
5.右面是一个长方体盒子的展开图。(单位:厘米)
6.如图是一个长方体的展开图,求出这个长方体的表面积
和体积。(单位:厘米)
8-6=2(厘米)
14-2×2=10(厘米)
表面积:(2×6+2×
10+6×10)×2=184(平方厘米)
体积:2×6×10=120(立方厘米)
5×5=25 cm
3×2=6 cm
=(25×6+6×7+25×7)×2
S=(ab+ah+bh)×2
=(150+42+175)×2
= 367×2
= 734(cm?)
答:至少需要734cm?的塑料纸。
7.一小包纸巾的长宽高如图所示。用一大张塑料纸将这10包纸巾包起来。至少需要多大面积的塑料纸?(单位:cm)
8.一个长方体水箱的内部长3 m、宽2 m、高3 m,向这个水
箱里注入15 m3的水。
(1)将一块石头浸没在这个水箱中,水位上升了????????????,水箱与
水接触的面积增加了多少?
?
(2)这块石头的体积是多少立方米?
????????×????????????=????????(m)
?
(3+2)×2×????????=????????(m2)
?
答:水箱与水接触的面积增加了???????? m2。
?
15÷(3×2)=????????(m)
?
解析:用水的体积除以容器的底面积求出原来水箱中水的高度,由水位上升????????????可知水位上升原来水箱中水的高度的????????????,进而求出水位上升的高度。要求水箱与水接触的面积增加了多少,就是求长为3 m,宽为2 m,高为水位上升的高度的长方体的侧面积。
?
(1)将一块石头浸没在这个水箱中,水位上升了????????????,水箱与水接触的面积增加了多少?
?
(2)这块石头的体积是多少立方米?
????????+????????=????????????(m) ????????????<3 水未溢出
?
3×2×????????=????????(m3)
?
答:这块石头的体积是???????? m3。
?
解析:首先要判断放入石头后,水是否溢出。可以比较放入石头后水箱的水面高度与容器的高,如果小于或等于,那么水未溢出;如果大于,那么水就溢出。因为????????+????????=????????????(m),????????????<3,所以水未溢出,再根据上升部分水的体积=石头的体积进行解答。
?
同学们都知道“乌鸦喝水”的故事吧!一个正方体的水
槽里装了一些水,旁边有物体挡住,乌鸦只能够到水槽的最上沿,在水槽的旁边有三块大小不同的石头。你能选择其中的两块石头,帮助乌鸦喝到水吗?
20×20×(20-18)=800(cm3)
358+454=812(cm3)
137+358=495(cm3)
137+454=591(cm3)
812>800>591>495
答:选择②号和③号这两块石头。
拓展提升
2.一盒杏脯的外包装如图所示。方阿姨要用一张包装纸把3
盒这样的杏脯包起来,至少需要多大面积的包装纸?(接
口处忽略不计)
4×3=12(cm)
(25×15+25×12+15×12)×2=1710(cm2)
答:至少需要1710 cm2的包装纸。
长方体
整理与复习
长方体和正方体的表面积计算方法
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
空间与图形
长方体和正方体的特征
露在外面的面
面增加(或减少)的规律
长方体有6个面,相对的面的面积相等,12条棱,相对的四条棱长度相等,8个顶点。
正方体有6个面,12条棱,12条棱长度都相等,8个顶点,6个面都是正方形,6个面的面积都相等。
我们会算长方体和正方体的体积了,怎么算球体的体积呢?
长方体和正方体的体积与棱长有关,球体的体积与球的半径有关。球的体积计算公式是V=????????????????????,R是球的半径。这个公式同学们在以后的学习中会学到。
?
要点1:长方体与正方体的特征
名称
联系
长方体
正方体
6个面
相同点
不同点
面的形状
面的大小
棱的长度
长方体
正方体
正方体是特殊的长方体
长方形;也可能两个相对面是正方形
相对的面的面积相等
12条棱分3组,每组中棱的长度相等
6个面都是正方形
6个面面积都相等
12条棱长都相等
8个顶点
12条棱
知识回顾
要点2:正方体的展开图
长方体展开图口诀
“一四一”“一三二”,
“一”在同层可任意,
“三个二”成阶梯,
“二个三”“日”相连,
异层必有“日”,
“凹”“田”不能有,
掌握此规律,运用定自如。
知识回顾
要点3:长方体和正方体的表面积
长方体的表面积 =(长×宽+长×高+宽×高)×2
=长×宽×2 +长×高×2 +宽×高×2
正方体的表面积 =棱长×棱长×6
=一个面的面积×6
长方体或正方体6个面的总面积,叫作它的表面积。
注意:在求物体表面积的时候,要根据具体的情况决定求几个面的面积之和。
知识回顾
要点4:露在外面的面
露在外面的面的个数是有规律的。?
用n表示正方体的个数:??
平放一排?????
露在外面的面=3n+2?
竖放一列?????
露在外面的面=4n+1
知识回顾
要点5:长方体和正方体的体积
如果用字母V表示体积,用字母a、b、h分别表示长方体的长、宽、高。
V=a×b×h
=abh
a
b
h
如果用字母V表示体积,用字母a表示正方体的棱长。
V=a×a×a
=a?
a
知识回顾
高级单位变为低级单位:数字会变大,高级单位的数×进率
低级单位变为高级单位:数字会变小,低级单位的数÷进率
1m3=1000dm3
1dm3=1000cm3
1L =1000mL
1L=1dm3
1mL=1cm3
1m3=1000000cm3
要点6:单位换算
知识回顾
1.想一想,填一填。
(1)一个药水瓶的容积是200( 毫升 ),一个仓库的占地
面积是300( 平方米 ),一个集装箱的体积约是40( 立
方米 )。
(2)280 mL=( 280 )cm3=( 0.28 )dm3
毫升
平方米
立
方米
280
0.28
6.24 m3=( 6240 )dm3
(3)有5个棱长是2 dm的正方体堆在墙角处,露在外面的面积
是( 44 )dm2。
6240
44
课堂练习
2.选一选。
(1)若一个长方体长3 cm,宽3 cm,高5 cm,则棱长是3 cm
的棱有( C )条。
A.4
B.6
C.8
D.18
(2)下列展开图沿虚线折叠后不能围成一个长方体的是
( B )。
A
B
C
D
C
B
(3)①是由36个完全相同的小正方体堆成的,把①推倒后
变成②,再利用这堆小正方体在③上4个4个地往上堆成一
栋“大楼”,这栋“大楼”的层数为( D )层。
A.12
B.4
C.6
D.9
D
3.一个长方体水池,底面长12 dm,宽6 dm。如果要向这个
水池里注入2 dm高的水,需要多少升水?
12×6×2=144(dm3)
144 dm3=144 L
答:需要144 L水。
4.李师傅想焊接一个无盖长方体铁皮煤箱,准备从如图8块
废旧铁皮中挑选5块使用,李师傅应该挑选哪5块铁皮?
(铁板厚度忽略不计)(单位:cm)
答:李师傅应该选③④⑤⑥⑦这5块铁皮。
=(12×10+12×8+10×8)×2
S=(ab+ah+bh)×2
=(120+96+80)×2
= 296×2
= 592(cm?)
5.右面是一个长方体盒子的展开图。(单位:厘米)
(1)长方体盒子的表面积是多少平方厘米?
答:盒子的表面积是592平方厘米。
=12×10×8
=120×8
=960(cm?)
V=abh
(2)长方体的体积是多少立方厘米?
答:长方体的体积是960立方厘米。
5.右面是一个长方体盒子的展开图。(单位:厘米)
6.如图是一个长方体的展开图,求出这个长方体的表面积
和体积。(单位:厘米)
8-6=2(厘米)
14-2×2=10(厘米)
表面积:(2×6+2×
10+6×10)×2=184(平方厘米)
体积:2×6×10=120(立方厘米)
5×5=25 cm
3×2=6 cm
=(25×6+6×7+25×7)×2
S=(ab+ah+bh)×2
=(150+42+175)×2
= 367×2
= 734(cm?)
答:至少需要734cm?的塑料纸。
7.一小包纸巾的长宽高如图所示。用一大张塑料纸将这10包纸巾包起来。至少需要多大面积的塑料纸?(单位:cm)
8.一个长方体水箱的内部长3 m、宽2 m、高3 m,向这个水
箱里注入15 m3的水。
(1)将一块石头浸没在这个水箱中,水位上升了????????????,水箱与
水接触的面积增加了多少?
?
(2)这块石头的体积是多少立方米?
????????×????????????=????????(m)
?
(3+2)×2×????????=????????(m2)
?
答:水箱与水接触的面积增加了???????? m2。
?
15÷(3×2)=????????(m)
?
解析:用水的体积除以容器的底面积求出原来水箱中水的高度,由水位上升????????????可知水位上升原来水箱中水的高度的????????????,进而求出水位上升的高度。要求水箱与水接触的面积增加了多少,就是求长为3 m,宽为2 m,高为水位上升的高度的长方体的侧面积。
?
(1)将一块石头浸没在这个水箱中,水位上升了????????????,水箱与水接触的面积增加了多少?
?
(2)这块石头的体积是多少立方米?
????????+????????=????????????(m) ????????????<3 水未溢出
?
3×2×????????=????????(m3)
?
答:这块石头的体积是???????? m3。
?
解析:首先要判断放入石头后,水是否溢出。可以比较放入石头后水箱的水面高度与容器的高,如果小于或等于,那么水未溢出;如果大于,那么水就溢出。因为????????+????????=????????????(m),????????????<3,所以水未溢出,再根据上升部分水的体积=石头的体积进行解答。
?
同学们都知道“乌鸦喝水”的故事吧!一个正方体的水
槽里装了一些水,旁边有物体挡住,乌鸦只能够到水槽的最上沿,在水槽的旁边有三块大小不同的石头。你能选择其中的两块石头,帮助乌鸦喝到水吗?
20×20×(20-18)=800(cm3)
358+454=812(cm3)
137+358=495(cm3)
137+454=591(cm3)
812>800>591>495
答:选择②号和③号这两块石头。
拓展提升
2.一盒杏脯的外包装如图所示。方阿姨要用一张包装纸把3
盒这样的杏脯包起来,至少需要多大面积的包装纸?(接
口处忽略不计)
4×3=12(cm)
(25×15+25×12+15×12)×2=1710(cm2)
答:至少需要1710 cm2的包装纸。
