北师大版五年级年级下册数学4.7 有趣的测量课件(共23张PPT)
文档属性
| 名称 | 北师大版五年级年级下册数学4.7 有趣的测量课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 17:38:23 | ||
图片预览



文档简介
(共23张PPT)
有趣的测量
北师大版五年级数学下册
第四单元 长方体(二)
结合具体活动情境,经历测量石块体积的过程,探索不规则物体体积的计算方法。
掌握测量不规则物体体积的计算方法,能根据实际情况测量不规则物体的体积。
在实践与探究中,尝试用多种方法解决问题,感受数学知识之间的相互联系,体会数学与生活的密切联系。
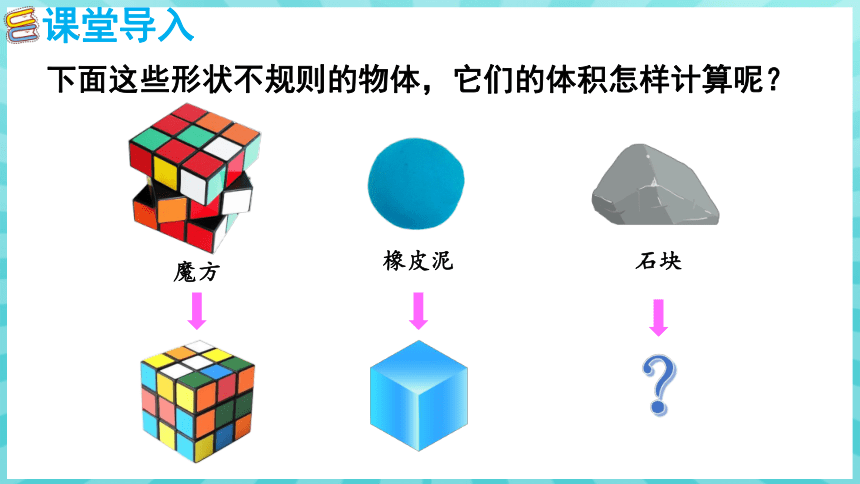
下面这些形状不规则的物体,它们的体积怎样计算呢?
橡皮泥
魔方
石块
?
如下图,要测量石块的体积,你有什么方法?与同伴交流。
不能直接用公式,怎么办呢?
10
15
10
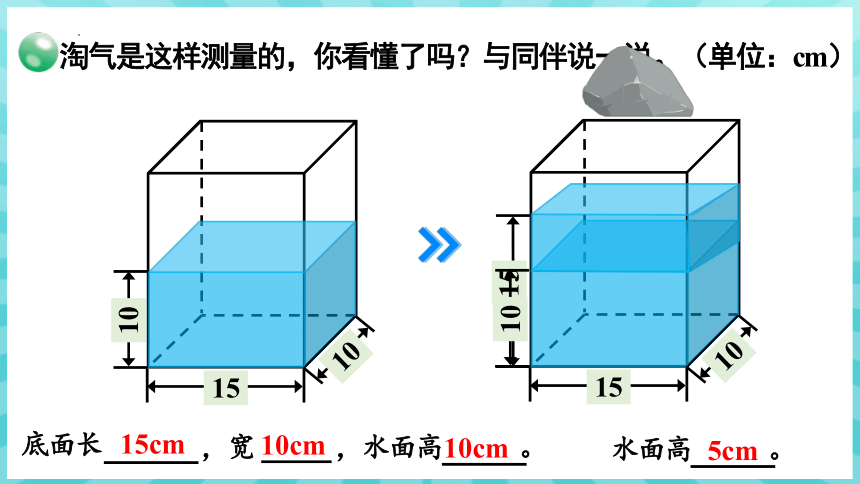
淘气是这样测量的,你看懂了吗?与同伴说一说。(单位:cm)
15
15
10
10
底面长
,宽
,水面高 。
15cm
水面高 。
10cm
10cm
5cm
10
15
10
15
15
10
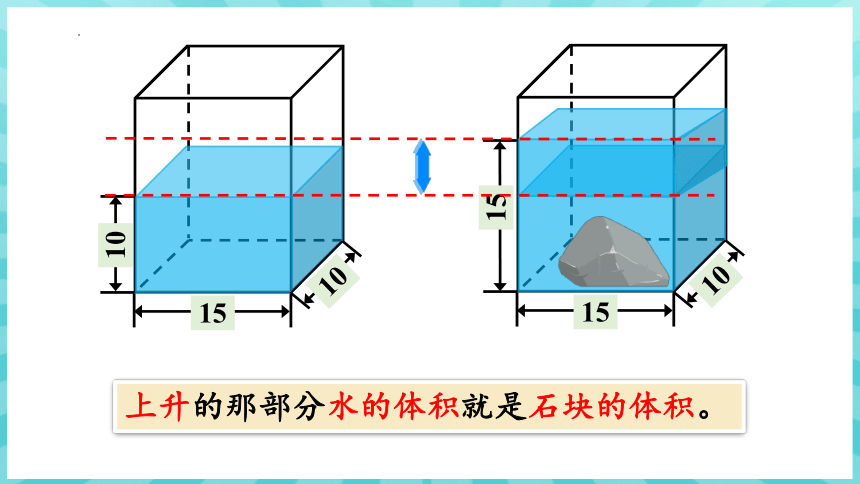
上升的那部分水的体积就是石块的体积。
10
15
10
15
15
10
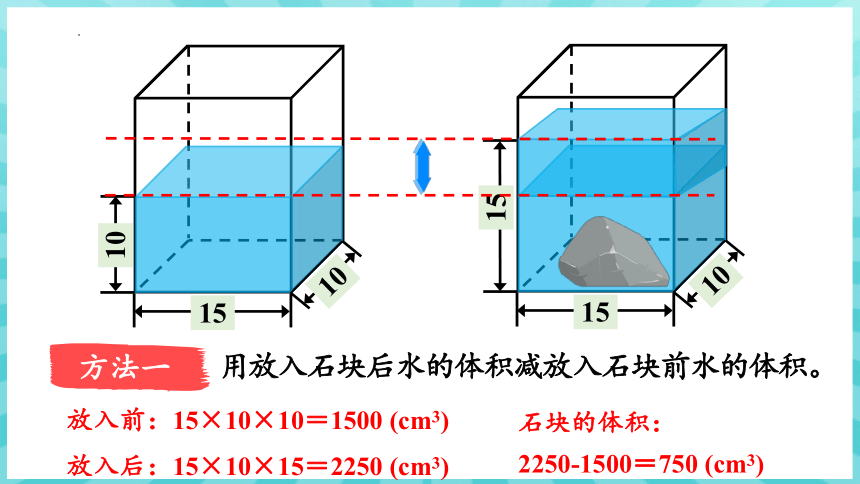
方法一
用放入石块后水的体积减放入石块前水的体积。
放入前:15×10×10=1500 (cm3)
放入后:15×10×15=2250 (cm3)
石块的体积:
2250-1500=750 (cm3)
10
15
10
15
15
10
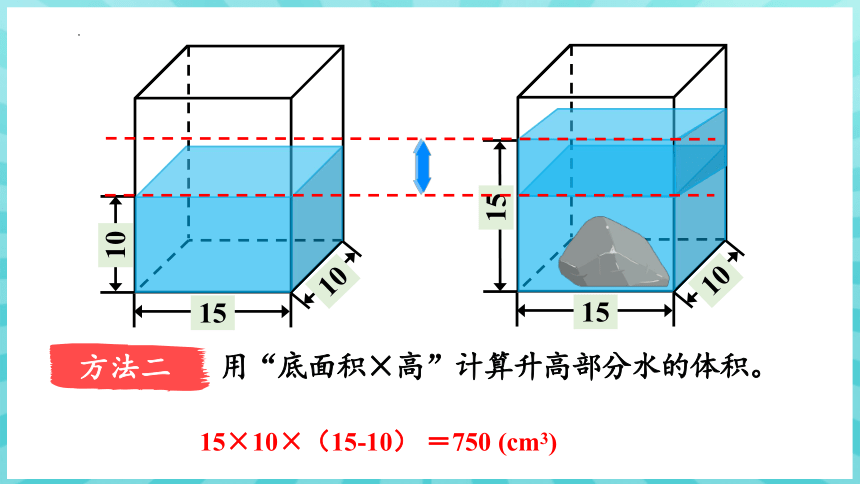
方法二
用“底面积×高”计算升高部分水的体积。
15×10×(15-10) =750 (cm3)
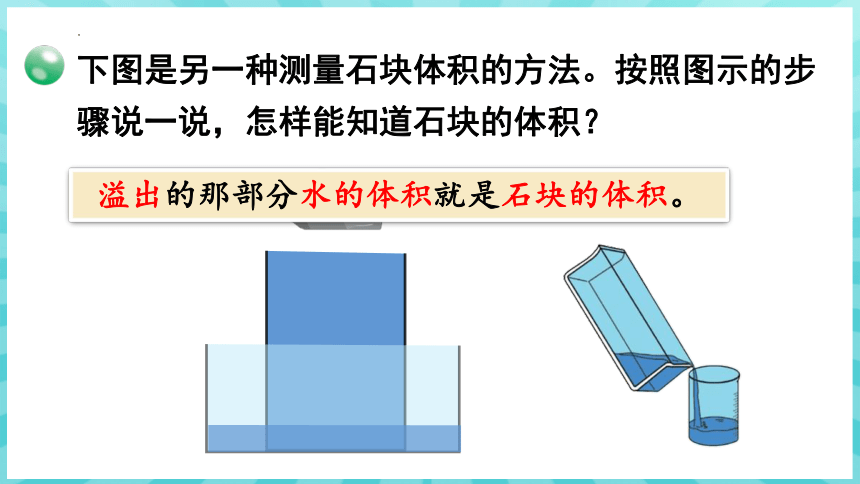
下图是另一种测量石块体积的方法。按照图示的步骤说一说,怎样能知道石块的体积?
容器里盛满水
放入石块
测量溢出的水
溢出的那部分水的体积就是石块的体积。
生活中还有哪些物品可以用上面的方法测量它的体积?在测量时需要注意什么问题?小组交流讨论。
水一定要没过所要测量的物体
用排水法求不规则物体的体积需要记录哪些数据?
用量筒或烧杯测量并记录原有水的体积。
将不规则物体没入水中,用量筒或烧杯测量并记录水和不规则物体的总体积。
02
01
回顾与反思
答:这块石头的体积是17 cm3。
72-55=17(mL)
这块石头的体积是多少?
1.
17 mL=17 cm3
石头放入前 石头放入后
水面上升的部分的体积就是土豆的体积。
2×1.5×0.2
= 3×0.2
= 0.6(dm3)
答:这个土豆的体积是0.6 dm3 。
一个长方体容器,底面长 2 dm、宽 1.5 dm,放入一个土豆后水面升高了 0.2 dm,这个土豆的体积是多少?
2.
将 2 个西红柿浸没在盛了 250 mL 水的量杯后,水位上升至600 mL,平均每个西红柿的体积是多少立方厘米?
3.
水面上升的部分的体积是 2 个西红柿体积。
600-250 = 350( mL )
350÷2 = 175(mL)
175 mL = 175 cm3
(600-250)÷2
=350÷2
=175(mL)
=175(cm3)
答:平均每个西红柿的体积是175立方厘米。
方法一
方法二
数 100 粒黄豆,放入一个盛有一定量水的量杯中,根据水面的升高情况,测量出体积,再算出一粒黄豆的体积。
怎样测量一粒黄豆的体积?与同伴交流,说一说你的想法。
4.
一个底面为正方形的长方体容器,底面边长为5cm,里面装有一些水和一个铁块,取出铁块后水面下降了4cm,铁块的体积是多大?
5.
5×5×4
=25×4
=100(cm )
答:铁块的体积是100立方厘米。
水面下降的部分的体积就是铁块的体积。
原正方体容器内水面的高:48÷(4×4)=3(dm)
48L=48dm
现在水面的高:3+0.5=3.5(dm)
答:现在水面的高是3.5分米。
有一个正方体容器,棱长为4dm,里面有48L水,如果把一块棱长为2dm的正方体铁块完全浸入水中,现在水面的高是多少分米?
6.
正方体铁块的体积是水面上升的部分的体积。
水面上升部分的高=体积÷正方体容器的底面积
水面上升部分的高:2×2×2÷(4×4)=0.5(dm)
7.一个长方体容器,从里面量长、宽均为3 dm,高为6 dm,里
面盛满了水,把一个西瓜浸没在水中,水溢出后再把西瓜拿出
来,这时量得容器内水深为50 cm,这个西瓜的体积是多少立
方分米?
50 cm=5 dm
3×3×(6-5)=9(dm3)
答:这个西瓜的体积是9 dm3。
1.有一个装水的长方体容器,底面积为100平方厘米,水深是
10厘米。如果将一个底面积是20平方厘米的长方体铁块竖直放
入水中至容器底部(水未溢出),但铁块仍有部分露在外面,
现在水深是多少厘米?
100×10=1000(立方厘米)
1000÷(100-20)=12.5(厘米)
答:现在水深是12.5厘米。
拓展提升
一个长方体玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果投入一块棱长4dm的正方体铁块,缸里的水溢出多少升?
2.
6.4 升
4×4×4=64 dm
8×6×(4-2.8)=57.6 dm
8 dm
6 dm
4 dm
2.8 dm
4 dm
64-57.6=6.4 dm
铁块体积
上升部分水的体积
溢出的水的体积
传说两千多年前,一位国王命令金匠制造一顶纯金的皇冠。皇冠制好后,他怀疑里面掺有银子,便请阿基米德鉴定一下。解决这个问题需要测量出皇冠的体积,阿基米德一直解决不了这个难题。
数学文化
有一天,阿基米德跨进浴池洗澡时,看见水溢到池外,于是他从中受到启发:可以通过排出水的体积确定皇冠的体积!从而判断皇冠是否掺有银子。他非常兴奋地从浴池里跳出去,赤身奔跑回家中。边跑边欢呼:“尤里卡!尤里卡!”(希腊语,意思是“我找到了!”)完全沉浸在新发现之中的阿基米德,竟然忘记了自己没穿衣服!
测量不规则物体的体积——液面升高法、溢水法
这节课你有什么收获
水面升高(下降)部分的体积或满杯时溢出的水的体积,就是不规则物体的体积。
有趣的测量
北师大版五年级数学下册
第四单元 长方体(二)
结合具体活动情境,经历测量石块体积的过程,探索不规则物体体积的计算方法。
掌握测量不规则物体体积的计算方法,能根据实际情况测量不规则物体的体积。
在实践与探究中,尝试用多种方法解决问题,感受数学知识之间的相互联系,体会数学与生活的密切联系。
下面这些形状不规则的物体,它们的体积怎样计算呢?
橡皮泥
魔方
石块
?
如下图,要测量石块的体积,你有什么方法?与同伴交流。
不能直接用公式,怎么办呢?
10
15
10
淘气是这样测量的,你看懂了吗?与同伴说一说。(单位:cm)
15
15
10
10
底面长
,宽
,水面高 。
15cm
水面高 。
10cm
10cm
5cm
10
15
10
15
15
10
上升的那部分水的体积就是石块的体积。
10
15
10
15
15
10
方法一
用放入石块后水的体积减放入石块前水的体积。
放入前:15×10×10=1500 (cm3)
放入后:15×10×15=2250 (cm3)
石块的体积:
2250-1500=750 (cm3)
10
15
10
15
15
10
方法二
用“底面积×高”计算升高部分水的体积。
15×10×(15-10) =750 (cm3)
下图是另一种测量石块体积的方法。按照图示的步骤说一说,怎样能知道石块的体积?
容器里盛满水
放入石块
测量溢出的水
溢出的那部分水的体积就是石块的体积。
生活中还有哪些物品可以用上面的方法测量它的体积?在测量时需要注意什么问题?小组交流讨论。
水一定要没过所要测量的物体
用排水法求不规则物体的体积需要记录哪些数据?
用量筒或烧杯测量并记录原有水的体积。
将不规则物体没入水中,用量筒或烧杯测量并记录水和不规则物体的总体积。
02
01
回顾与反思
答:这块石头的体积是17 cm3。
72-55=17(mL)
这块石头的体积是多少?
1.
17 mL=17 cm3
石头放入前 石头放入后
水面上升的部分的体积就是土豆的体积。
2×1.5×0.2
= 3×0.2
= 0.6(dm3)
答:这个土豆的体积是0.6 dm3 。
一个长方体容器,底面长 2 dm、宽 1.5 dm,放入一个土豆后水面升高了 0.2 dm,这个土豆的体积是多少?
2.
将 2 个西红柿浸没在盛了 250 mL 水的量杯后,水位上升至600 mL,平均每个西红柿的体积是多少立方厘米?
3.
水面上升的部分的体积是 2 个西红柿体积。
600-250 = 350( mL )
350÷2 = 175(mL)
175 mL = 175 cm3
(600-250)÷2
=350÷2
=175(mL)
=175(cm3)
答:平均每个西红柿的体积是175立方厘米。
方法一
方法二
数 100 粒黄豆,放入一个盛有一定量水的量杯中,根据水面的升高情况,测量出体积,再算出一粒黄豆的体积。
怎样测量一粒黄豆的体积?与同伴交流,说一说你的想法。
4.
一个底面为正方形的长方体容器,底面边长为5cm,里面装有一些水和一个铁块,取出铁块后水面下降了4cm,铁块的体积是多大?
5.
5×5×4
=25×4
=100(cm )
答:铁块的体积是100立方厘米。
水面下降的部分的体积就是铁块的体积。
原正方体容器内水面的高:48÷(4×4)=3(dm)
48L=48dm
现在水面的高:3+0.5=3.5(dm)
答:现在水面的高是3.5分米。
有一个正方体容器,棱长为4dm,里面有48L水,如果把一块棱长为2dm的正方体铁块完全浸入水中,现在水面的高是多少分米?
6.
正方体铁块的体积是水面上升的部分的体积。
水面上升部分的高=体积÷正方体容器的底面积
水面上升部分的高:2×2×2÷(4×4)=0.5(dm)
7.一个长方体容器,从里面量长、宽均为3 dm,高为6 dm,里
面盛满了水,把一个西瓜浸没在水中,水溢出后再把西瓜拿出
来,这时量得容器内水深为50 cm,这个西瓜的体积是多少立
方分米?
50 cm=5 dm
3×3×(6-5)=9(dm3)
答:这个西瓜的体积是9 dm3。
1.有一个装水的长方体容器,底面积为100平方厘米,水深是
10厘米。如果将一个底面积是20平方厘米的长方体铁块竖直放
入水中至容器底部(水未溢出),但铁块仍有部分露在外面,
现在水深是多少厘米?
100×10=1000(立方厘米)
1000÷(100-20)=12.5(厘米)
答:现在水深是12.5厘米。
拓展提升
一个长方体玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果投入一块棱长4dm的正方体铁块,缸里的水溢出多少升?
2.
6.4 升
4×4×4=64 dm
8×6×(4-2.8)=57.6 dm
8 dm
6 dm
4 dm
2.8 dm
4 dm
64-57.6=6.4 dm
铁块体积
上升部分水的体积
溢出的水的体积
传说两千多年前,一位国王命令金匠制造一顶纯金的皇冠。皇冠制好后,他怀疑里面掺有银子,便请阿基米德鉴定一下。解决这个问题需要测量出皇冠的体积,阿基米德一直解决不了这个难题。
数学文化
有一天,阿基米德跨进浴池洗澡时,看见水溢到池外,于是他从中受到启发:可以通过排出水的体积确定皇冠的体积!从而判断皇冠是否掺有银子。他非常兴奋地从浴池里跳出去,赤身奔跑回家中。边跑边欢呼:“尤里卡!尤里卡!”(希腊语,意思是“我找到了!”)完全沉浸在新发现之中的阿基米德,竟然忘记了自己没穿衣服!
测量不规则物体的体积——液面升高法、溢水法
这节课你有什么收获
水面升高(下降)部分的体积或满杯时溢出的水的体积,就是不规则物体的体积。
