北师大版五年级下册数学第九单元总复习 图形与几何 课件(共27张PPT)
文档属性
| 名称 | 北师大版五年级下册数学第九单元总复习 图形与几何 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 18:07:42 | ||
图片预览





文档简介
(共27张PPT)
图形与几何(1)
总复习
北师版数学五年级(下)
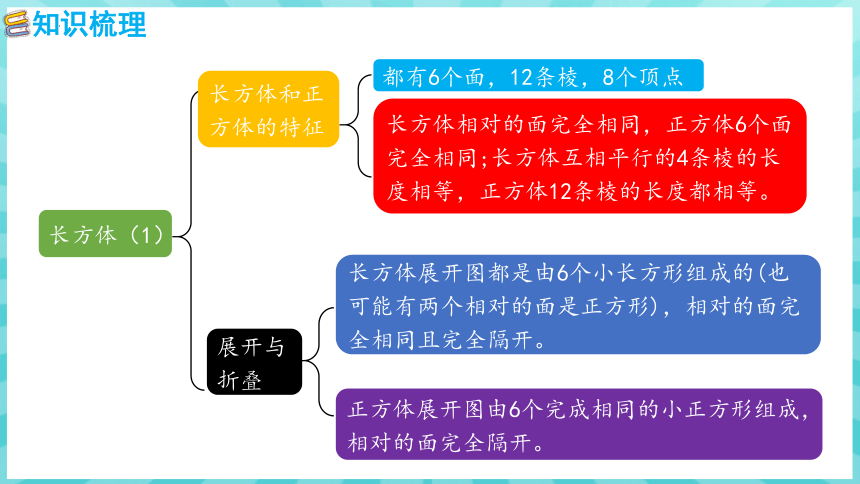
长方体(1)
展开与折叠
长方体展开图都是由6个小长方形组成的(也可能有两个相对的面是正方形),相对的面完全相同且完全隔开。
正方体展开图由6个完成相同的小正方形组成,相对的面完全隔开。
长方体和正方体的特征
都有6个面,12条棱,8个顶点
长方体相对的面完全相同,正方体6个面完全相同;长方体互相平行的4条棱的长度相等,正方体12条棱的长度都相等。
长方体(1)
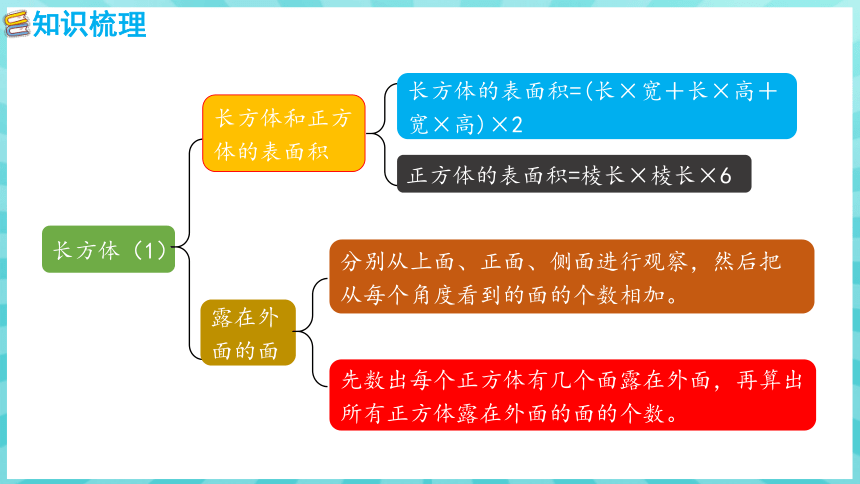
露在外面的面
分别从上面、正面、侧面进行观察,然后把从每个角度看到的面的个数相加。
先数出每个正方体有几个面露在外面,再算出所有正方体露在外面的面的个数。
长方体和正方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
商与被除数的大小关系
分数除法
意义
一个数除以一个非零数的计算方法
“已知一个数的几分之几是多少,求这个数”的解题方法
长方体(2)
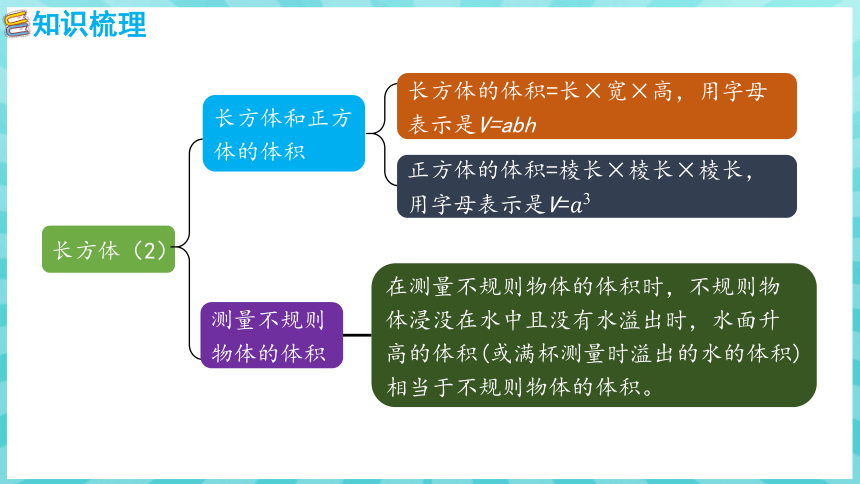
测量不规则物体的体积
在测量不规则物体的体积时,不规则物体浸没在水中且没有水溢出时,水面升高的体积(或满杯测量时溢出的水的体积)相当于不规则物体的体积。
长方体和正方体的体积
长方体的体积=长×宽×高,用字母表示是V=abh
正方体的体积=棱长×棱长×棱长,用字母表示是V=
商与被除数的大小关系
分数除法
意义
一个数除以一个非零数的计算方法
“已知一个数的几分之几是多少,求这个数”的解题方法
1.长方体和正方体的特征
长方体的特征有哪些?什么是长方体长、宽、高?
有8个顶点;有6个面,相对的面形状、大小都相同;有12条棱,相对的棱的长度相等。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
重点回顾
1.长方体和正方体的特征
正方体的特征有哪些?正方体与长方体有什么关系?
有8个顶点; 6个面都是相同的正方形;12条棱的长度都相等。
正方体是长、宽、高都相等的特殊长方体。
重点回顾
1.长方体和正方体的特征
如何求长方体和正方体棱长的总和?
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
重点回顾
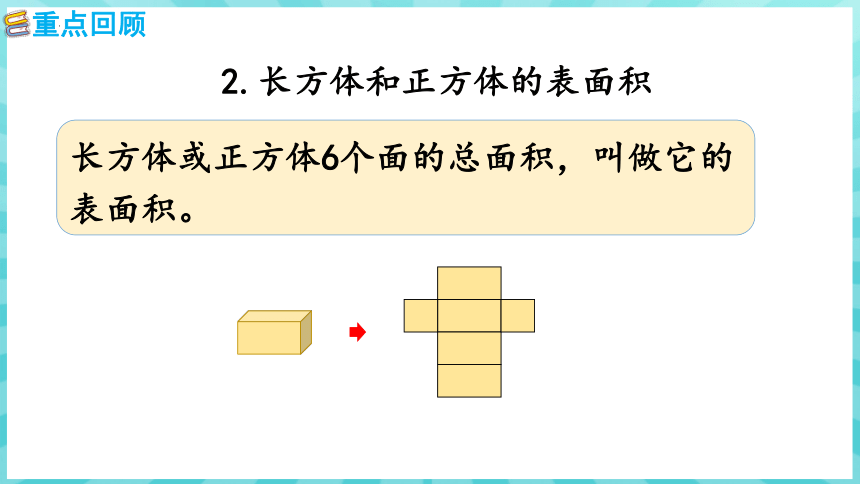
2.长方体和正方体的表面积
长方体或正方体6个面的总面积,叫做它的表面积。
重点回顾
2.长方体和正方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示为S=2(ab+ah+bh)
长方体表面积的计算方法是什么?
重点回顾
2.长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示为S=6
正方体表面积的计算方法是什么?
重点回顾
3.体积和体积单位
物体所占空间的大小叫作物体的体积。
常用的体积单位有立方米、立方分米、立方厘米,用字母分别表示为 。
重点回顾
4.容积和容积单位
容器所能容纳物体的体积,叫作它们的容积。
容积的单位有升和毫升,用字母分别表示为L和mL。
重点回顾
5.体积单位间的进率
1=1000, 1=1000c。
5=( )
9000=( )d。
5000
9
重点回顾
5.体积单位间的进率
1L=1000mL 1000mL=1L
1L=1 1mL=1
重点回顾
6.长方体和正方体的体积
长方体的体积=长×宽×高,字母公式为V=abh。
正方体的体积=棱长×棱长×棱长,字母公式为V=。
长方体和正方体体积的统一公式:
长方体(或正方体)的体积=底面积×高
字母公式为V=Sh。
重点回顾
7.用排水法测量不规则物体的体积
将物体完全浸入盛有水的规则容器中,如果没有水溢出,那么上升的那部分水的体积等于水中物体的体积。
重点回顾
1.填一填。
(1)一支钢笔一次能吸12( mL )墨水,一个哈密瓜的体
积大约是8( dm3 )。
(2)在( )中填上合适的数。
2.9 mL=( 2.9 )cm3
1.4 L=( 1400 ) mL
0.03 dm3=( 30 )cm3
700 cm3=( 0.7 )dm3
mL
dm3
2.9
1400
30
0.7
课堂练习
(3)如图是一个长方体纸盒的展开图。(单位:cm)
①与b面相对的面是( f )面。
②做这个纸盒至少需要纸板( 348 )cm2。
③这个纸盒的体积是( 432 )cm3。
f
348
432
(4)如图是由若干个棱长为1 cm的小正方体搭成的立体图
形,它的体积是( 9 )cm3。如果分别从正面和上面看,
所看到的图形面积之和是( 11 )cm2。
2.一块正方体钢块的棱长为7分米,这块正方体钢块的体积是
多少立方分米?
7×7×7=343(立方分米)
答:这块正方体钢块的体积是343立方分米。
9
11
3.学校礼堂长20 米、宽15 米、高8 米,要粉刷礼堂的顶
棚和四周墙壁,除去门窗面积120 平方米,平均每平方米
用涂料0.15千克,一共需要涂料多少千克?
(20×15+20×8+15×8)×2-20×15=860(平
方米)
860-120=740(平方米)
740×0.15=111(千克)
答:一共需要涂料111千克。
4.下面的长方形木板中,哪两块是从同一个长方体上拆下
来的?原来长方体的体积是多少?(单位:cm)
64×43×75=206400(cm3)
答:①和③是从同一个长方体上拆下来的,原来长方体
的体积是206400 cm3。
5.计算下面图形的表面积和体积。(单位:cm)
表面积:10×10×6+5×5×4=700(cm2)
体积:10×10×10-5×5×5=875(cm3)
解析:图形的表面积=大正方体的表面积+小正方体4个侧面的面
积,图形的体积=大正方体的体积-小正方体的体积。
6.一个长方体玻璃鱼缸(无盖),长50 cm、宽40 cm、
高30 cm。(玻璃的厚度忽略不计)
(1)做这个鱼缸至少需要玻璃多少平方厘米?
(2)在鱼缸里注入30 L水,再往水里放入鹅卵石、水草和
鱼,这时水面高度是25 cm(水全部没过鹅卵石、水草和
鱼),这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
(1)做这个鱼缸至少需要玻璃多少平方厘米?
50×40+(50×30+40×30)×2=7400(cm2)
答:做这个鱼缸至少需要玻璃7400 cm2。
(2)在鱼缸里注入30 L水,再往水里放入鹅卵石、水草和
鱼,这时水面高度是25 cm(水全部没过鹅卵石、水草和
鱼),这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
50×40×25=50000(cm3)
30 L=30 dm3=30000 cm3
50000-30000=20000(cm3)
答:这些鹅卵石、水草和鱼的体积一共是20000 cm3。
7.在一个长4 dm、宽3 dm、高2 dm的长方体容器里放一块
石头,再加满水(石头完全没入水中)。然后再将石头取出来,这时水面下降到1.8 dm处。这块石头的体积是多少立方分米?
4×3×(2-1.8)=2.4(dm3)
答:这块石头的体积是2.4 dm3。
点拨:石头的体积就是下降的水的体积,即长方体容器的底面积乘水面下降的高度。
1.一个长方体木块,将长锯掉3 cm后就成了一个正方体,已知
锯掉后得到的正方体比原来长方体的表面积减少了60 cm2,求
正方体的体积。
正方体的棱长:60÷4÷3=5(cm)
正方体的体积:5×5×5=125(cm3)
答:正方体的体积是125 cm3。
拓展提升
2.一个长方体,如果高增加2 cm,那么就成为一个正方体
了,这时表面积比原来增加了56 cm2。原来长方体的体积是多少立方厘米?
56÷4÷2=7(cm)
7×7×(7-2)=245(cm3)
答:原来长方体的体积是245 cm3。
解析:由题意可知,长方体的底面是一个正方形且高比底面边长少2 cm,表面积增加的部分是高为2 cm的4个侧面的面积,由此可以求出一个侧面的面积,进而求出底面的边长。
图形与几何(1)
总复习
北师版数学五年级(下)
长方体(1)
展开与折叠
长方体展开图都是由6个小长方形组成的(也可能有两个相对的面是正方形),相对的面完全相同且完全隔开。
正方体展开图由6个完成相同的小正方形组成,相对的面完全隔开。
长方体和正方体的特征
都有6个面,12条棱,8个顶点
长方体相对的面完全相同,正方体6个面完全相同;长方体互相平行的4条棱的长度相等,正方体12条棱的长度都相等。
长方体(1)
露在外面的面
分别从上面、正面、侧面进行观察,然后把从每个角度看到的面的个数相加。
先数出每个正方体有几个面露在外面,再算出所有正方体露在外面的面的个数。
长方体和正方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
商与被除数的大小关系
分数除法
意义
一个数除以一个非零数的计算方法
“已知一个数的几分之几是多少,求这个数”的解题方法
长方体(2)
测量不规则物体的体积
在测量不规则物体的体积时,不规则物体浸没在水中且没有水溢出时,水面升高的体积(或满杯测量时溢出的水的体积)相当于不规则物体的体积。
长方体和正方体的体积
长方体的体积=长×宽×高,用字母表示是V=abh
正方体的体积=棱长×棱长×棱长,用字母表示是V=
商与被除数的大小关系
分数除法
意义
一个数除以一个非零数的计算方法
“已知一个数的几分之几是多少,求这个数”的解题方法
1.长方体和正方体的特征
长方体的特征有哪些?什么是长方体长、宽、高?
有8个顶点;有6个面,相对的面形状、大小都相同;有12条棱,相对的棱的长度相等。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
重点回顾
1.长方体和正方体的特征
正方体的特征有哪些?正方体与长方体有什么关系?
有8个顶点; 6个面都是相同的正方形;12条棱的长度都相等。
正方体是长、宽、高都相等的特殊长方体。
重点回顾
1.长方体和正方体的特征
如何求长方体和正方体棱长的总和?
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
重点回顾
2.长方体和正方体的表面积
长方体或正方体6个面的总面积,叫做它的表面积。
重点回顾
2.长方体和正方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示为S=2(ab+ah+bh)
长方体表面积的计算方法是什么?
重点回顾
2.长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示为S=6
正方体表面积的计算方法是什么?
重点回顾
3.体积和体积单位
物体所占空间的大小叫作物体的体积。
常用的体积单位有立方米、立方分米、立方厘米,用字母分别表示为 。
重点回顾
4.容积和容积单位
容器所能容纳物体的体积,叫作它们的容积。
容积的单位有升和毫升,用字母分别表示为L和mL。
重点回顾
5.体积单位间的进率
1=1000, 1=1000c。
5=( )
9000=( )d。
5000
9
重点回顾
5.体积单位间的进率
1L=1000mL 1000mL=1L
1L=1 1mL=1
重点回顾
6.长方体和正方体的体积
长方体的体积=长×宽×高,字母公式为V=abh。
正方体的体积=棱长×棱长×棱长,字母公式为V=。
长方体和正方体体积的统一公式:
长方体(或正方体)的体积=底面积×高
字母公式为V=Sh。
重点回顾
7.用排水法测量不规则物体的体积
将物体完全浸入盛有水的规则容器中,如果没有水溢出,那么上升的那部分水的体积等于水中物体的体积。
重点回顾
1.填一填。
(1)一支钢笔一次能吸12( mL )墨水,一个哈密瓜的体
积大约是8( dm3 )。
(2)在( )中填上合适的数。
2.9 mL=( 2.9 )cm3
1.4 L=( 1400 ) mL
0.03 dm3=( 30 )cm3
700 cm3=( 0.7 )dm3
mL
dm3
2.9
1400
30
0.7
课堂练习
(3)如图是一个长方体纸盒的展开图。(单位:cm)
①与b面相对的面是( f )面。
②做这个纸盒至少需要纸板( 348 )cm2。
③这个纸盒的体积是( 432 )cm3。
f
348
432
(4)如图是由若干个棱长为1 cm的小正方体搭成的立体图
形,它的体积是( 9 )cm3。如果分别从正面和上面看,
所看到的图形面积之和是( 11 )cm2。
2.一块正方体钢块的棱长为7分米,这块正方体钢块的体积是
多少立方分米?
7×7×7=343(立方分米)
答:这块正方体钢块的体积是343立方分米。
9
11
3.学校礼堂长20 米、宽15 米、高8 米,要粉刷礼堂的顶
棚和四周墙壁,除去门窗面积120 平方米,平均每平方米
用涂料0.15千克,一共需要涂料多少千克?
(20×15+20×8+15×8)×2-20×15=860(平
方米)
860-120=740(平方米)
740×0.15=111(千克)
答:一共需要涂料111千克。
4.下面的长方形木板中,哪两块是从同一个长方体上拆下
来的?原来长方体的体积是多少?(单位:cm)
64×43×75=206400(cm3)
答:①和③是从同一个长方体上拆下来的,原来长方体
的体积是206400 cm3。
5.计算下面图形的表面积和体积。(单位:cm)
表面积:10×10×6+5×5×4=700(cm2)
体积:10×10×10-5×5×5=875(cm3)
解析:图形的表面积=大正方体的表面积+小正方体4个侧面的面
积,图形的体积=大正方体的体积-小正方体的体积。
6.一个长方体玻璃鱼缸(无盖),长50 cm、宽40 cm、
高30 cm。(玻璃的厚度忽略不计)
(1)做这个鱼缸至少需要玻璃多少平方厘米?
(2)在鱼缸里注入30 L水,再往水里放入鹅卵石、水草和
鱼,这时水面高度是25 cm(水全部没过鹅卵石、水草和
鱼),这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
(1)做这个鱼缸至少需要玻璃多少平方厘米?
50×40+(50×30+40×30)×2=7400(cm2)
答:做这个鱼缸至少需要玻璃7400 cm2。
(2)在鱼缸里注入30 L水,再往水里放入鹅卵石、水草和
鱼,这时水面高度是25 cm(水全部没过鹅卵石、水草和
鱼),这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
50×40×25=50000(cm3)
30 L=30 dm3=30000 cm3
50000-30000=20000(cm3)
答:这些鹅卵石、水草和鱼的体积一共是20000 cm3。
7.在一个长4 dm、宽3 dm、高2 dm的长方体容器里放一块
石头,再加满水(石头完全没入水中)。然后再将石头取出来,这时水面下降到1.8 dm处。这块石头的体积是多少立方分米?
4×3×(2-1.8)=2.4(dm3)
答:这块石头的体积是2.4 dm3。
点拨:石头的体积就是下降的水的体积,即长方体容器的底面积乘水面下降的高度。
1.一个长方体木块,将长锯掉3 cm后就成了一个正方体,已知
锯掉后得到的正方体比原来长方体的表面积减少了60 cm2,求
正方体的体积。
正方体的棱长:60÷4÷3=5(cm)
正方体的体积:5×5×5=125(cm3)
答:正方体的体积是125 cm3。
拓展提升
2.一个长方体,如果高增加2 cm,那么就成为一个正方体
了,这时表面积比原来增加了56 cm2。原来长方体的体积是多少立方厘米?
56÷4÷2=7(cm)
7×7×(7-2)=245(cm3)
答:原来长方体的体积是245 cm3。
解析:由题意可知,长方体的底面是一个正方形且高比底面边长少2 cm,表面积增加的部分是高为2 cm的4个侧面的面积,由此可以求出一个侧面的面积,进而求出底面的边长。
